유리 렌즈의 열 성형 공정 조건 도출을 위한 수치해석 연구

1. 서론

최근 렌즈는 광학센서, 카메라, 레이저 시스템, 의학, 항공우주, 군사 등의 영상 데이터 활용을 위해 다양한 산업에 사용되고 수요도 증가하고 있다. 그에 따라 높은 광학 성능을 갖는 렌즈를 위해서 다양한 연구가 진행되고 있다. 렌즈는 다양한 재질과 금형을 통해 여러 형상으로 생산을 할 수 있다. 렌즈에는 구면과 비구면 렌즈가 있는데, 비구면 렌즈는 구면 렌즈에서 발생되는 구면 수차의 문제를 개선시킨 렌즈로 많이 사용되고 있다[1]. 과거 유리 소재의 비구면 렌즈는 절삭, 연삭 등의 기계 가공으로 생산하여 성능은 우수하지만 대량으로 생산하기에는 양산성이 낮은 문제점이 있었다. 이를 보완을 하기 위해 초정밀 금형에 고온, 고압 조건에서 유리 성형 공정(Glass Molding Process, GMP)으로 양산성을 높이고 있으나, 세계 시장에서는 일본 및 독일의 업체가 시장을 독점하고 있어서 국산화 기술 및 개발이 필요하다[1,2].

GMP 공정은 순차이송형과 일괄처리 방식으로 두 가지 공정이 있다. 순차이송형 방식은 가열, 압축, 냉각 단계를 하나 또는 다수의 Cavity가 있는 금형에 유리 소재를 넣어서 가열, 압축, 냉각 단계로 순차적으로 각 단계별로 이동되면서 진행하는 방식이다. 각 부품이 개별적으로 진행됨으로 정교한 조절이 가능하여 고품질의 렌즈를 얻을 수 있고, 각 단계에 장비 변경이 상대적으로 빠른 장점이 있다. 하지만, 각 부품이 순차적으로 이동하므로 생산 속도가 상대적으로 느리고, 순차적으로 이동이 필요하기 때문에 자동화가 어려운 단점이 있다.

일괄처리 방식은 환경 챔버 내에서 진공 또는 질소 환경에서 가열, 압축, 냉각 단계를 일괄적으로 동시에 진행하는 공정이다. 공정이 동시에 진행하여 대량 생산과 생산 속도가 빠르고, 여러 과정이 동시에 진행됨에 따라 자동화가 용이하다. 이 방식에서는 각 부품의 개별적인 조절에 대한 제어시스템이 중요하며, 라인 변경 시에는 전체를 조절해야 하는 어려움이 있다.

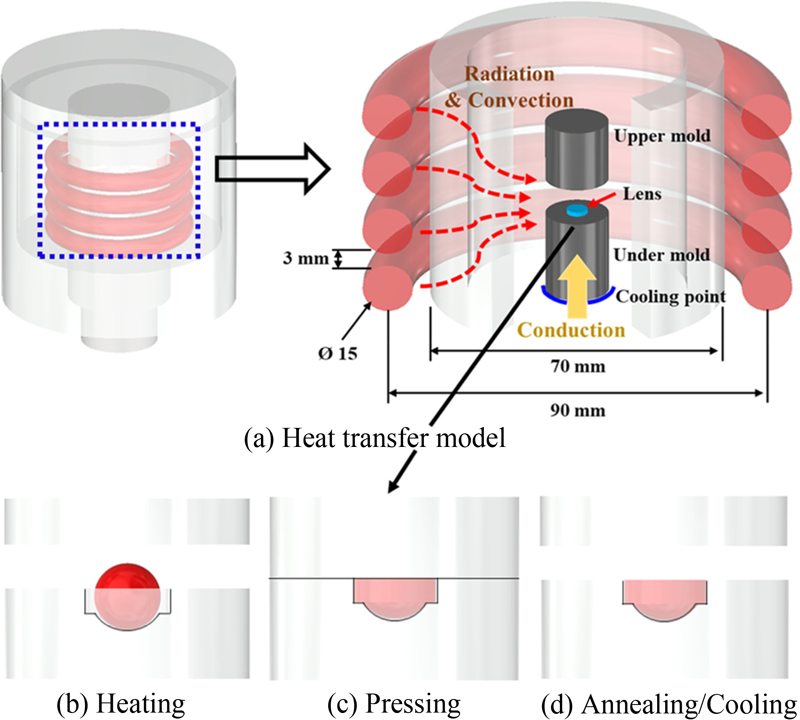
본 연구에서는 대량 생산과 생산속도를 고려하여 일괄처리 방식에 대하여 연구하였으며, 순차이송형 및 일괄처리 방식의 개략도와 유리 성형 공정의 각 단계에서 렌즈의 이상적인 온도 변화에 대해서 Fig. 1에 나타냈다.

Fig. 1

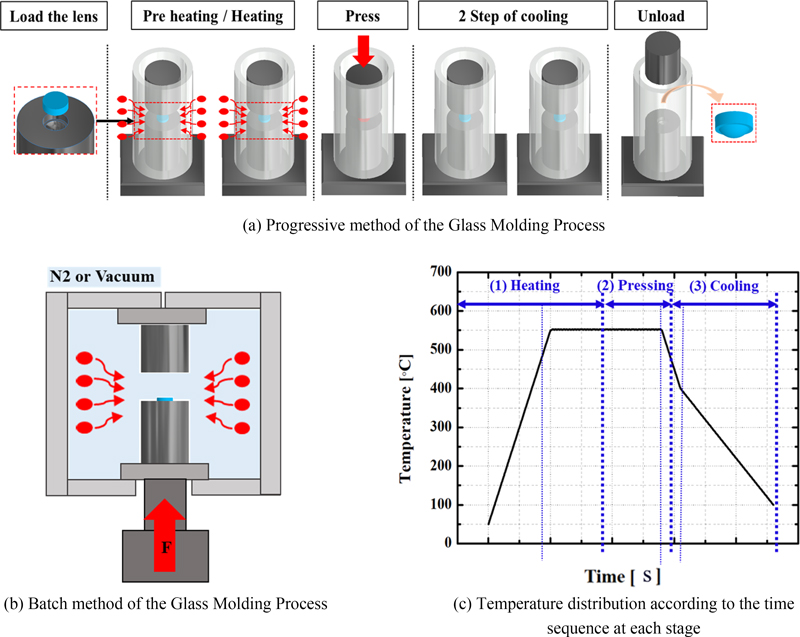
Schematic of glass molding process and temperature of lens at each step (heating, pressing, cooling)

GMP 공정에 대한 기존의 연구와 최신 연구는 다양하게 연구되고 있다. Lee 등은 순차이송형 방식에서 비구면 렌즈 금형에 대한 열전달과 열응력 해석을 수행하였다. 접촉면 사이에 관한 열전달 계수와 금형에 발생하는 압력을 분석으로 금형에 의한 손상이 없음을 규명하였으나, 가열시스템에 의한 렌즈의 온도변화 해석을 하지 않았다[3]. Jung 등은 다구치 실험계획법으로 렌즈 금형의 수명, 유지보수 주기, 생산성 등을 고려한 최적의 양산 조건에 대하여 연구하였으며, 유리 성형 과정의 요인 고려하는 어려움을 바탕으로 냉각과정만을 분석하였다[4]. Ryu 등은 금형 코어에 자중물을 이용한 자중 성형 공정에서 성형 온도와 스텝 시간을 상용화된 장비를 이용하여 실험적으로 분석하였으며, 성형 온도와 스텝 시간의 상관관계를 통해 목표치의 렌즈중심 두께에 도달하는 조건 도출과 금형 코어 수명이 증가한다고 규명하였다[5]. Kim 등은 상용화 장비를 이용하여 칼로겐유리를 사용하여 회절비구면렌즈 구조를 갖는 금형 코어에 다양한 온도를 적용하여 압축 성형에 대해 연구하였다. 성형 온도에 의한 에어 갭, 부분 압축에 의한 압력 및 하중의 표면 결함에 상관관계를 분석하여 표면 결함이 적게 발생하는 칼로겐 유리 렌즈 성형이 가능하다고 규명하였다[6]. Son 등은 칼로겐 유리 렌즈 성형 공정에서 결함 발생하는 가열 조건과 열 해석에 관해 연구하였다. 높은 성형 온도와 긴 시간의 가열 시간이 표면 결함에 상관있음을 도출하였으나, 가열조건에서만의 영향을 분석하고 압축, 냉각 과정은 장비를 이용하여 진행하였다[7]. Dambon 등은 렌즈 금형에 대해서 해석 프로그램과 상용화 장비를 이용하여 정확한 곡선을 갖는 금형 설계에 효과적인 금형 제조 방법을 연구하였다[8]. Yan 등은 렌즈 성형 공정에서 고온 열전달 및 점성 변형에 대해 이론과 상용화 장비 및 해석 프로그램을 통한 FEM 시뮬레이션으로 연구를 하였다. 열팽창 및 열전달 고려하여 불완전한 가열과 압축은 불균일한 렌즈 오차를 초래한다고 규명하였다[9]. Yao 등은 렌즈의 점탄성에 대한 탄성계수의 영향을 유리 성형 공정 시뮬레이션으로 연구하였으며, 온도의 증가와 점탄성 변화의 상관관계를 분석하고 실린더 압축 과정에서 온도에 따라 탄성 계수가 압축 변위와 잔류 응력에 대해 영향이 있다고 도출하였다[10]. Shu 등은 렌즈 변형 온도와 항복 온도에 대해서 탄성 특성과 고온에서의 열팽창 계수를 연구하였으며, 유한요소 해석을 통해 열역학적 변수의 정확성을 검증하였다[11]. 기존의 비구면 렌즈 성형 방법에 대해서 실험적, 수치해석 등으로 다양하게 연구가 진행되었다. 하지만, 대부분의 연구가 해외 장비 등을 이용한 연구가 많았으며, 장비 국산화에 관한 연구는 부족하다고 판단된다.

본 연구에서는 비구면 렌즈 성형 장비를 국산화하기 위한 기초연구로서, 일괄처리 방식의 비구면 렌즈 성형 공정에서 가열, 압축, 냉각과정에서 렌즈의 온도변화에 대해 연구하였다. 가열/압축/냉각 조건에 따른 렌즈 온도 분포 및 편차를 수치해석 프로그램을 이용하여 열역학적으로 분석하였다. 수치해석 프로그램의 열해석 모델 통해 렌즈의 허용 성형 온도를 달성하기 위한 가열 조건과 압축 시 가열 조건과 냉각 용량 조건에 대해 렌즈 온도의 상관관계를 분석하여, 국산화 장비를 위한 기초 연구를 하였다.

2. 수치해석

일괄처리 방식의 유리 성형 공정 장비에서 가열 조건에 따른 각 부품의 온도 분포와 렌즈의 온도 편차 등을 확인하기 위해 열 해석을 Ansys Fluent를 이용하여 수행하였다. 일괄처리 방식은 질소 또는 진공상태에서 가열시스템으로 렌즈를 가열하여 렌즈가 성형 온도에 도달하면 상 변화가 된 렌즈를 상부 또는 하부에서 가압하여 압축하고, 금형 틀에 있는 렌즈 형상으로 성형을 하고 냉각하여 렌즈를 추출하는 방식이다.

가열, 압력, 냉각의 단계에 따른 중요한 기술들이 적용되고 있으며, 유리 소재는 온도의 의존성이 매우 강한 소재임으로 가열 단계에서는 렌즈가 성형 허용 온도범위까지 도달 및 유지하기 위한 적합한 가열 구조와 조건이 필요하다. 실온에서의 유리는 단단하고 깨지기 쉬운 재료이나, 고온에서는 점탄성체 또는 점성 액체가 되며, 유리의 열 팽창도 고려해야 하는 중요한 요소이다[8]. 본 연구에서 사용된 렌즈는 L-BAL-35 (Ohara Corp. Kanagawa, Japan)이다. 유리 성형에서 렌즈 온도 범위에 대한 정의가 있으며, Table 1에 나타냈다. 변형점(StP)은 렌즈의 열팽창과 수축이 가장 민감한 온도이며, 이 온도 이하에서 유리 변형이 최소화된다. 어닐링 포인트(AP)는 렌즈를 가열하여 재료분자 구조를 재정렬하는 온도이다. 전이 온도(Tg)는 렌즈의 용융물의 부피가 느린 속도로 감소되는 온도이며, 유리 렌즈 성형은 항상 이 온도 이상에서 진행되어야 한다. 항복 온도(At)는 유리가 최대 팽창과 상대적으로 낮은 가소성에 도달하고 수축하기 시작하는 온도이다. 연화점(SP)은 유리가 액체처럼 거동하는 온도이다[8].

Table 1

Thermal expansion characteristics of glass L-BAL 35

본 연구에서 사용된 수치해석 3D 모델 및 열전달 모델과 수치 해석에 적용된 부품의 물성치를 Table 2와 Fig. 2에 나타냈다. 렌즈를 성형하기 위해 높은 온도로 가열을 하기 때문에 각 부품들은 고온에 적합한 재질로 선정하였다. 열 해석에서 실제 유리성형 공정의 가열 단계를 모델링하기 위해서 히터의 열량, 질소환경, 각 부품 물성치 등의 경계조건을 다양하게 고려해야 한다. 열 해석을 위한 수치해석 모델에서 가열 시스템은 석영 히터로 가정하고 Discrete Ordinates (DO)의 복사열 모델과 석영에 발열량을 적용하여 렌즈에 복사열과 전도열을 통한 렌즈의 온도변화를 분석하였다. DO 모델은 공간의 이산화와 각도의 이산화를 기반으로 한 복사열 모델이며, 이 모델은 복잡한 기하학적 구조나 다양한 복사열 조건을 가진 시스템에서도 정확한 복사열 해석이 가능하여 적용하였다[12].

Table 2

Properties of materials

Fig. 2

Numerical simulation 3-D model and heat transfer model

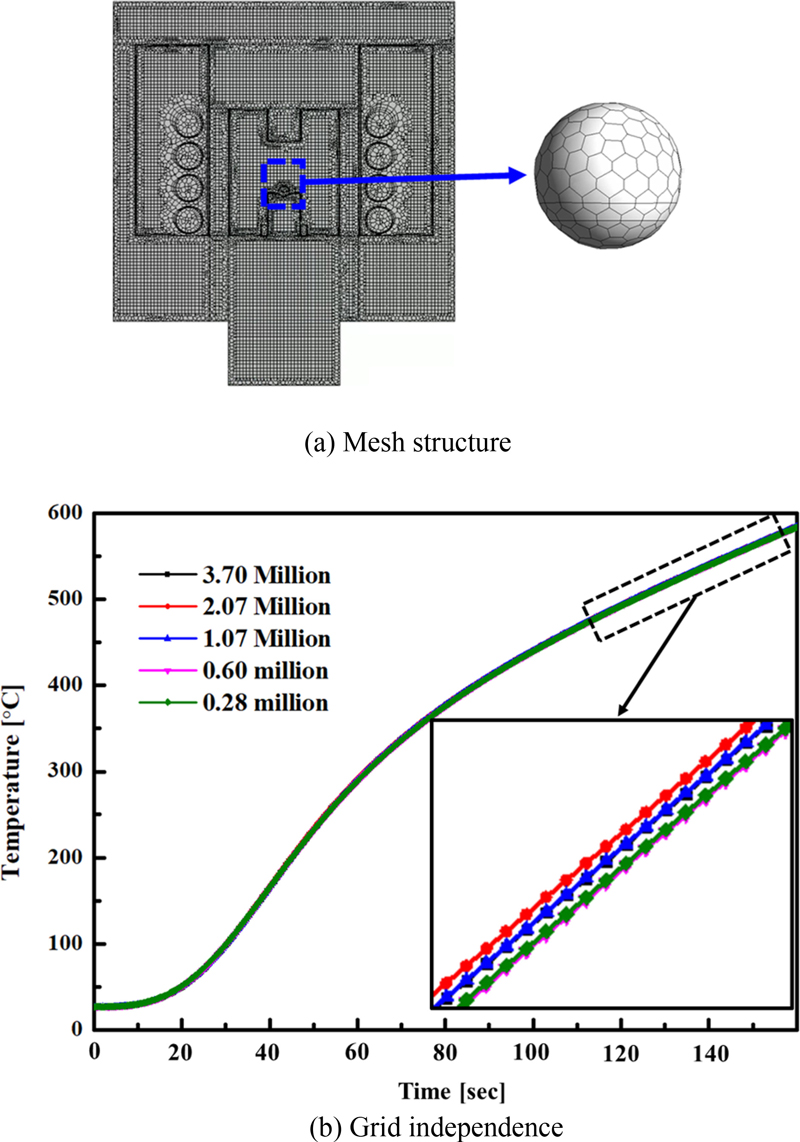
Fig. 3은 수치해석에서 격자 설계와 격자 수에 따른 해석 결과의 신뢰성을 확보하기 위해 격자 의존도에 대해 결과를 나타냈다. 격자는 Fluent Meshing에서 Poly Hexa-core로 격자를 설계하였으며, 격자 수를 280,000개와 3,700,000개의 범위 내에서 수행하여 렌즈의 온도를 비교하였다. 격자 수에 따라서 렌즈 온도 변화 차이는 최대 2.5°C로 나타났다. 전이 온도에 도달하는 이상적인 렌즈 온도 변화는 1,070,000개와 3,700,000개의 격자에서 나타났으며, 수치해석 시간 효율성을 위해 1,070,000개의 격자를 사용하였다.

Fig. 3

Mesh structure and grid independence

3. 결과 및 토의

3.1 가열 과정

본 연구에서는 일괄처리 방식 유리 성형 장비의 가열 조건에 따른 유리 소재의 전이 온도에 도달하는 것과 압축 성형의 렌즈 온도를 유지하는 것과 냉각 단계에서 냉각 성능에 대한 열 해석을 연구하였다.

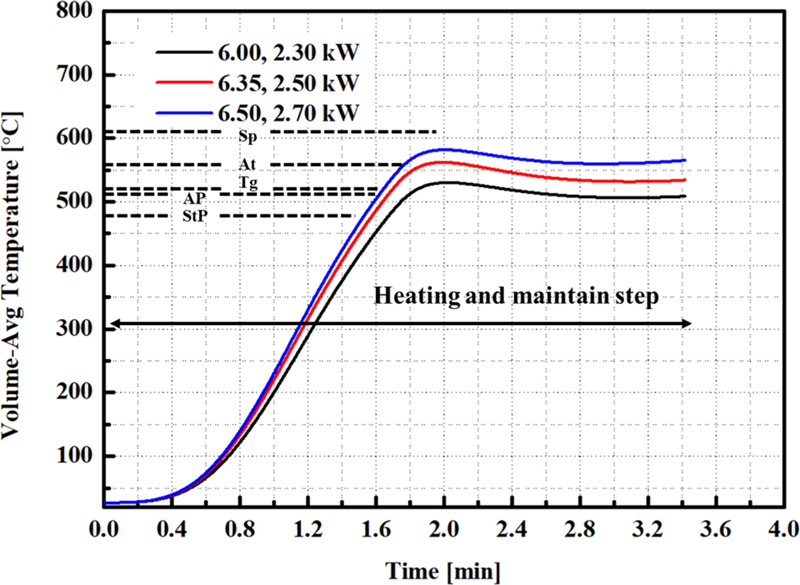
Fig. 4에서는 유리 소재에 석영으로 설계된 가열 시스템으로 가열 과정(Step 1)과 압축 성형하기 위한 렌즈 온도를 유지하는 과정(Step 2)에 대한 열 해석 결과를 나타냈다. 렌즈의 성질은 항복 온도(At)를 초과하기 시작하면 가소성이 발생됨으로 최대한 항복 온도를 초과하지 않는 것이 중요하다. Step 1의 초기 가열(Pre Heating) 단계를 100초로 설정하고[9], 6.00, 6.35, 6.50 kW의 열량에 대해 열 해석 하였다. 각 렌즈의 온도는 485.95, 520.42, 539.02°C로 도달하였다. 가열 과정 후 압축 과정을 진행하기 위해서는 렌즈 온도를 전이 온도 이상으로 유지가 필요해서, Step 2 과정을 105초 동안 가열시스템의 열량을 일정한 비율로 감소시켜 열 해석하였다. 가열 열량은 렌즈의 온도가 상승하지 않고 유지할 수 있는 열량을 2.30, 2.50, 2.70 kW로 적용하였다. 초반 구간은 기존의 축적된 열에 의해 렌즈 온도가 상승하여 전체적으로 전이 온도에 도달 및 초과를 한 후 시간의 경과에 따라 렌즈 온도가 유지되는 것으로 나타났다. 각 열량에 대해서는 렌즈 온도는 각각 508.6, 534.7, 565.4°C로 유지되었으며, 가열 열량 2.30 kW에서는 전이 온도 이상으로 렌즈 온도가 유지되지 못하였다. 2.50, 2.70 kW에서는 전이 온도 이상으로 유지되는 것을 분석할 수 있으나, 2.70 kW의 열량에서는 렌즈의 온도가 가소성이 발생할 수 있는 온도범위에 근접하는 것으로 분석되어 가열 열량으로 적합하지 않는 것으로 분석하였다.

Fig. 4

Comparison of the temperature change on lens at each heater system power in Step 1, 2

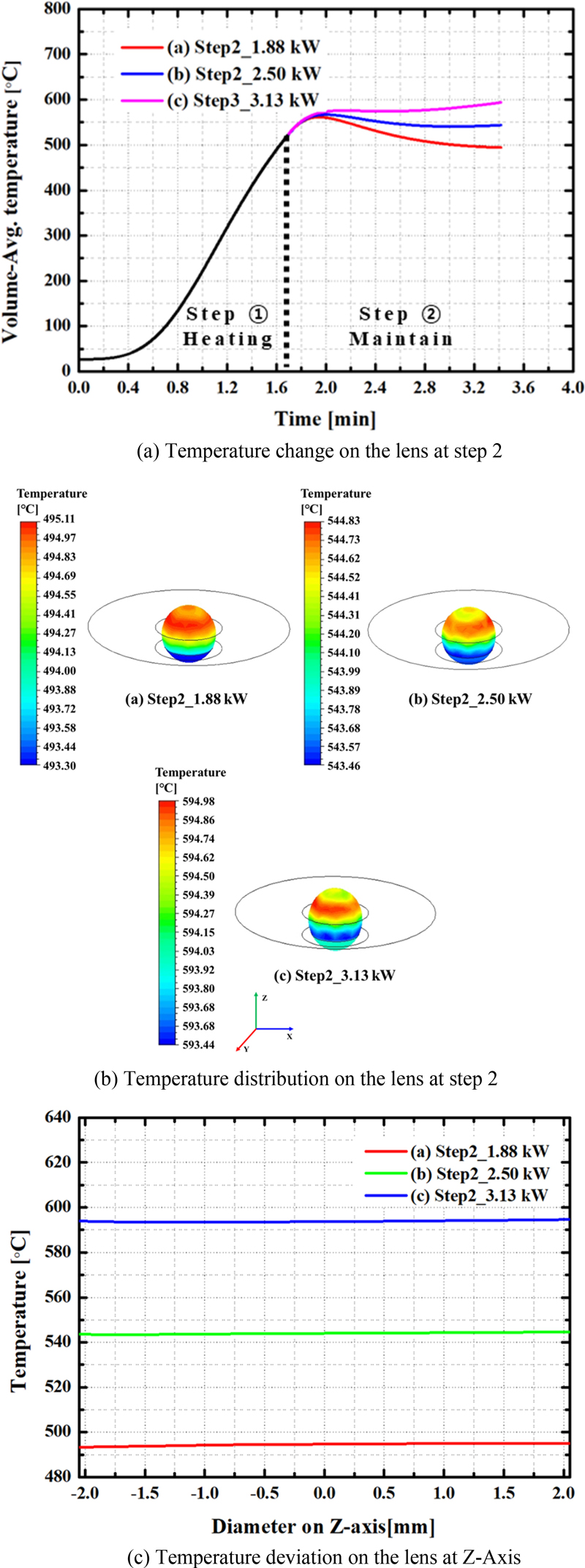
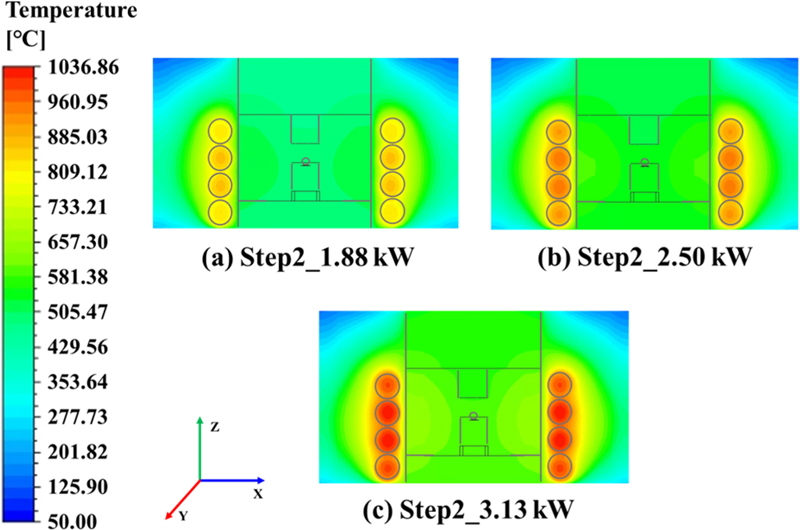
Fig. 5에서는 6.35 kW의 가열 과정 후 압축 과정을 진행하기 위해 렌즈 온도를 유지하는 과정이며, 가열 열량에 따른 렌즈 온도 분포와 Z축의 렌즈 온도 편차를 분석하였다. Fig. 5(a)에서는 가열 열량 2.50 kW를 105초 동안 일정한 비율로 증가, 감소한 가열 열량 값을 적용하여 렌즈 온도 변화 결과를 나타냈다. 압축 과정을 하기 위해서는 렌즈 온도의 유지가 중요하며, 2.50 kW 열량 외에서는 렌즈 온도 유지를 하지 못하고 온도가 증가 또는 감소하는 경향성을 나타냈다. 결과적으로 가열 과정에서는 6.35, 2.50 kW의 가열 열량으로 제어를 하는 것이 적합하다고 분석하였다.

Fig. 5

Comparison of the temperature distribution and deviation on the lens in step 2

Fig. 5(b)에서는 렌즈의 Step 2 과정 구간을 거친 렌즈 온도 분포를 나타냈다. 렌즈의 온도는 하부 금형(Mold)에 접촉되어 있는 부분에서 가열시스템에 의한 전도열에 지배적이고, 노출되어 있는 부분은 복사열과 대류에 지배적임으로 렌즈의 온도 편차가 발생한다. 전체적으로 렌즈 온도는 중심부를 기준으로 온도 편차는 X, Y축으로는 차이가 적게 나타나지만, Z축으로는 하부에서 상부로 전도와 복사열의 차이로 인해 발생되는 온도 편차가 나타나는 것을 확인할 수 있다. 렌즈의 온도 편차가 많이 발생할수록 렌즈의 광학 성능에 영향이 있기 때문에 렌즈 온도 편차를 최소화하는 가열 조건이 필요하다.

Fig. 5(c)에서는 가열시스템의 열량에 따라 Z축 방향으로 렌즈의 온도 편차를 나타냈으며, 최대 약 (a) 1.8°C, (b) 1.35°C, (c) 1.53°C로 전체적으로 2°C 이내로 분포되는 것을 분석하였다. 이 결과를 바탕으로 가열 과정에서 적합한 가열 열량은 6.35, 2.5 kW로 판단하였다.

Fig. 6에서는 렌즈를 제외한 가열시스템과 각 부품의 중심부 XZ면을 기준으로 온도 분포를 나타냈다. 전체적인 부품의 온도는 가열시스템의 열량에 따라서 동일한 경향성의 온도 분포를 갖는 것으로 나타났으며, 열 해석에 문제가 될만한 고온 이상(Hot Spot)과 같은 것은 발생하지 않았음을 볼 수 있다.

Fig. 6

Comparison of the environment temperature on total part after Step 2

3.2 압축 과정

압축 과정에서 균일하게 가열된 렌즈를 압축시켜 렌즈의 오차를 최소화하는 공정을 하는 것이 중요하지만, 본 연구에서는 압축 과정에서 균일한 압축과 압축 시 발생하는 열은 동일하다고 가정을 하고 압축 과정에서의 렌즈 온도를 유지하는 것에 대한 열 해석을 중점적으로 연구하였다.

Fig. 7에서는 Fig. 2(c) 압축(Pressing) 모델에 대하여 가열과정에서의 수치해석 데이터 및 온도를 적용하고, 렌즈 온도 유지를 위한 가열 열량에 따른 렌즈 온도 변화와 편차를 나타냈다. 압축과정에서는 렌즈의 압축과 압축 후 자연 냉각의 단계가 있다. Fig. 7(a)는 압축과정에서 전이 온도(Tg) 이상으로 유지하기 위해 60초 동안 1.52, 2.03, 2.54 kW 의 가열 열량을 적용하는 Step 3 과정과 자연 냉각의 Step 4 과정에 대한 렌즈 온도 변화를 나타냈다. 2.03 kW에서는 렌즈의 온도가 전이 온도 이상에서 일정하게 유지되는 경향성을 나타냈다. 하지만, 1.52, 2.54 kW에서는 렌즈의 온도가 유지되지 못하고 감소하거나 증가하는 경향성을 나타났으며, 렌즈의 온도가 전이 온도 이하 또는 가소성이 발생될 수 있는 온도 범위로 분포하기 때문에 렌즈의 광학 성능과 품질을 확보하기 위해 압축 과정(Step 3)에서는 2.03 kW가 적합한 가열 열량인 것을 열 해석으로 분석할 수 있다. Fig. 7(a)의 Step 4는 렌즈를 압축 성형 후 자연 냉각하는 과정이다. 가열된 렌즈를 바로 강제 대류 또는 전도 방식으로 냉각을 진행하면 렌즈의 분자 재정렬에서 문제, 결함, 균일성 등의 문제가 발생할 수 있다. 그리하여, 자연 냉각으로 천천히 냉각시켜서 렌즈를 냉각할 수 있는 상태로 만드는 과정을 적용해야 한다. Step 4는 가열시스템을 전체적으로 Off한 상태로 45초 동안의 자연 냉각을 진행하였다. 모든 가열 열량에서 렌즈 온도는 어닐링 포인트(AP) 온도 이하로 분포되는 것을 확인할 수 있다.

Fig. 7

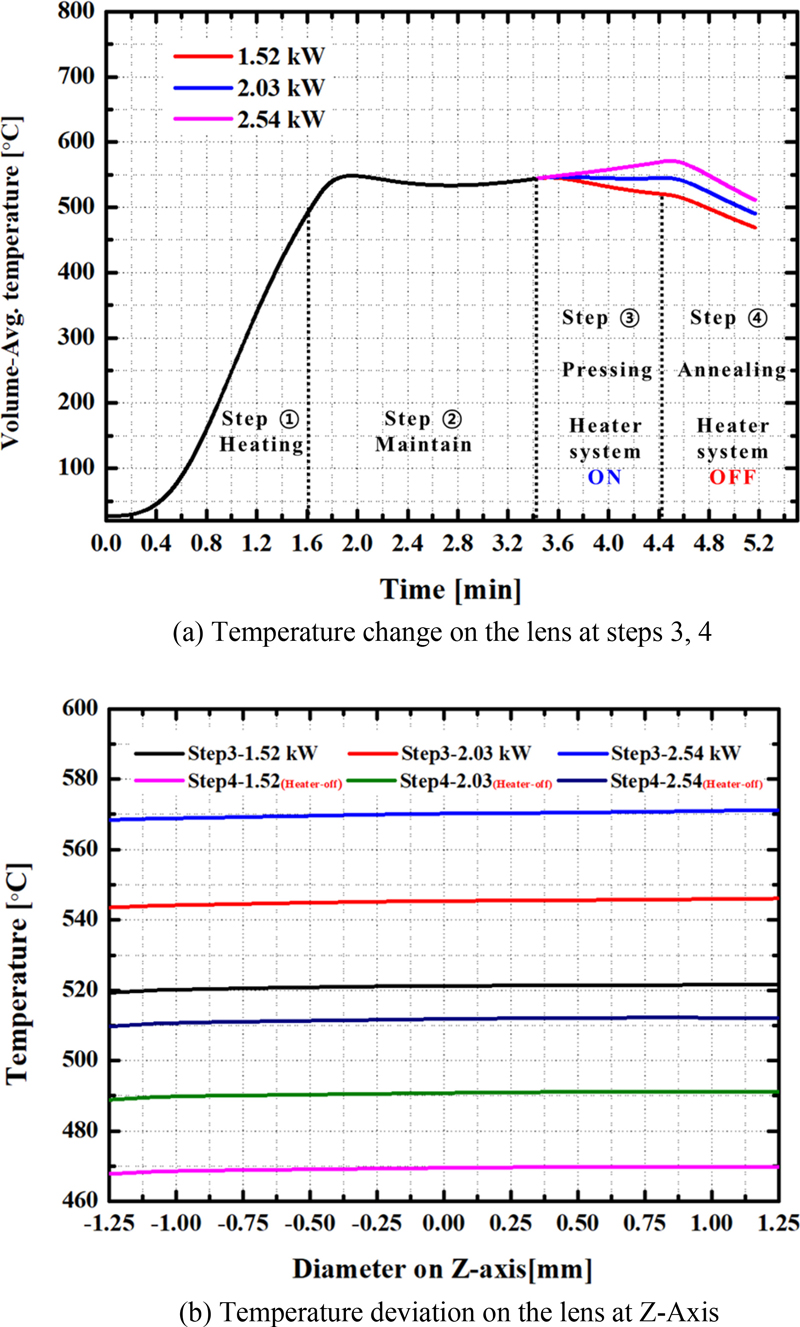
Comparison of the lens temperature change according to heater power in the pressing process of steps 3, 4

Fig. 7(b) 에서는 Steps 3, 4 과정에서 Z축의 렌즈 온도 편차를 나타냈다. Step 3 과정 후 각 가열 열량에 따른 렌즈 온도 편차는 약 2.32, 2.58, 2.85°C로 전체적으로 3°C 이내로 분포되었다. Step 3의 가열 과정 뒤에 Step 4의 자연 냉각 과정에서 렌즈 온도 편차는 1.5, 1.69, 1.88°C로 전체적으로 2°C 이내로 분포되었다. 이 과정에서의 렌즈 온도는 총 52.32, 55.53, 59.71°C의 온도 감소가 발생되었다. 이러한 압축 과정에서의 가열 열량에 따른 렌즈 온도를 유지하는 것과 자연 냉각에 의한 렌즈의 온도 편차가 적은 결과를 통해 압축 과정에서의 적합한 가열 용량은 2.03 kW로 판단하였다.

3.3 냉각 과정

냉각 과정은 압축 과정에 자연 냉각된 렌즈를 공랭, 수냉, 복합 방식 등의 다양한 방법으로 렌즈를 냉각하는 과정이다. 본 연구에서의 냉각 방식은 Fig. 2(a)에서 볼 수 있듯이, 하부 금형(Mold) 아랫면에 냉각 용량을 적용하여 냉각 해석을 진행하였다. 급속 냉각은 렌즈의 열 응력을 유발하여 광학적 성능을 저하시키고, 또한 소성 과정을 고려하지 않으면 냉각 중에 렌즈가 변형되거나 렌즈에 왜곡이 발생됨으로 급속 냉각이 되지 않는 조건 적용이 필요하다. 그리하여, 단계별 냉각으로 렌즈의 내부열 응력을 제어하고, 렌즈의 열팽창 계수와 열전도도를 파악하여 광학적 특성과 안정성을 확보하여 비구면 렌즈의 품질 및 광학 성능을 갖을 수 있는 냉각 조건 도출이 중요하다.

Fig. 8에서는 2단계의 냉각 과정 Steps 5, 6을 진행하여 렌즈의 온도 변화와 렌즈의 Z축에 대한 온도 편차에 대해서 나타냈다. Step 5 - 2.10 kW- 40초, Step 6 - 2.90 kW-100초 기준에 대해 일정 비율로 증가/감소된 냉각 용량으로 냉각 해석을 진행하였다.

Fig. 8

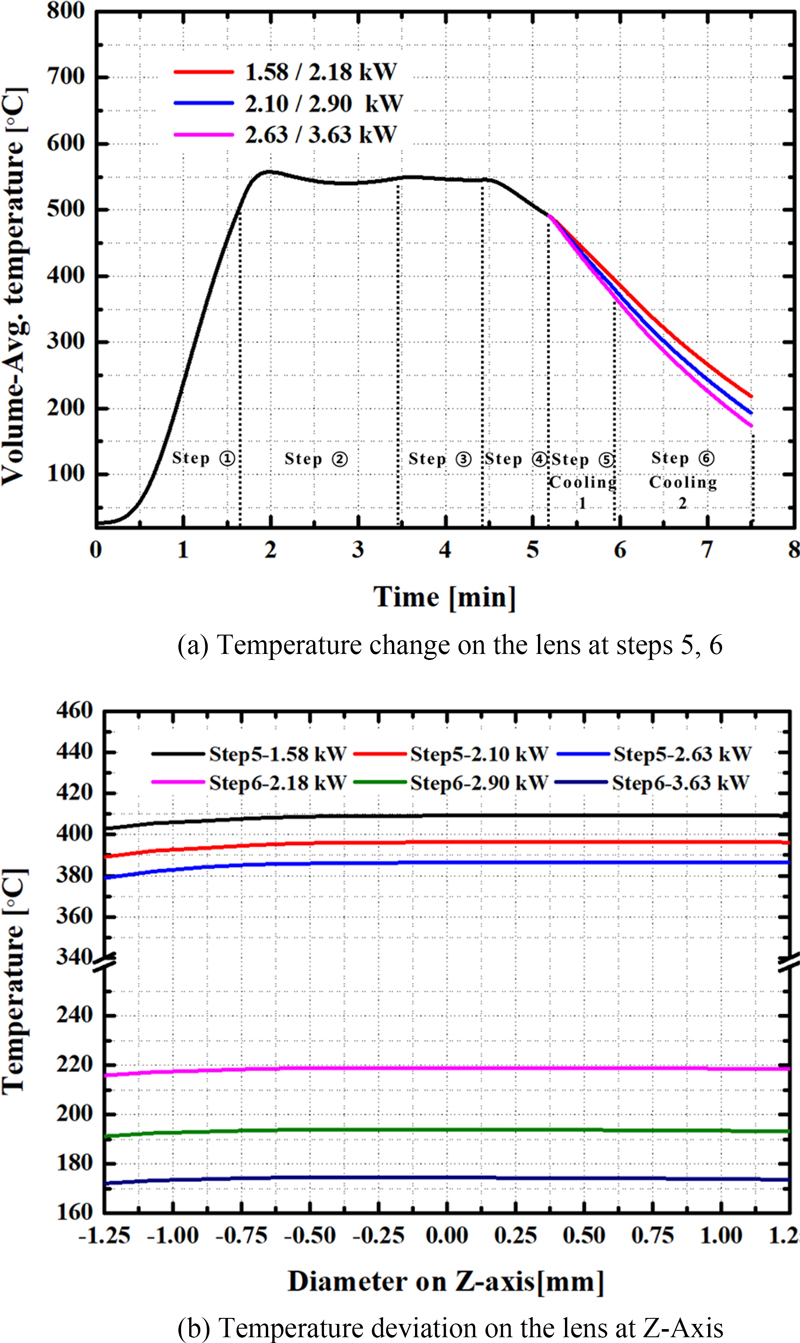
Comparison of the lens temperature change according to heater power in the cooling process of steps 5, 6

Fig. 8(a)에서 Step 5의 40초 동안 각 냉각 용량에 따른 렌즈 온도는 490.55°C에서 409.15, 396.19, 386.23°C로 감소되었다. Step 6의 100초 동안 각 냉각 용량에 따른 렌즈 온도 변화는 218.43, 193.24, 173.62°C로 앞의 과정에서 약 190-210°C의 온도 감소가 되었다. 전체적으로 렌즈 온도가 이상적으로 감소되는 것으로 판단되지만, 렌즈의 분자 재정렬을 위해 렌즈 온도 편차의 최소화가 중요하기 때문에 렌즈 온도 편차 분석이 필요하다.

Fig. 8(b)에서 Step 5 과정의 렌즈 온도 편차는 각각 6.39, 7.16, 7.48°C로 Steps 2-5 과정 중에서 가장 큰 온도 편차가 계산 되었다. 본 연구에서 설정한 시간에서는 냉각 용량을 증가시키는 것은 급냉의 조건을 적용하는 것과 동일하기 때문에 렌즈 온도 편차를 증가시키는 것으로 분석하였다. 이와 같은 렌즈 온도 편차는 렌즈 냉각 중에 열 응력, 왜곡 등을 문제를 발생시킬 수 있다. Step 5 과정에서 낮은 냉각 용량으로 렌즈의 분자 재정렬과 광학 성능의 품질을 가질 수 있도록 냉각하는 것이 적합한 것으로 분석하였다. Step 6 과정의 렌즈 온도 편차는 각각 2.66, 2.04, 1.54°C로 Step 5 과정에서의 온도 편차와 상대적인 경향성이 나타났다. 이는 렌즈의 온도가 낮아진 상태에서 높은 냉각 용량과 냉각 시간으로 전도에 의한 냉각 효과가 렌즈에 전체적으로 적용되는 것으로 분석할 수 있다. 이러한 냉각 해석을 통해서 전도 냉각 방식으로는 Step 5에서 낮은 냉각 용량과 Step 6에서 높은 냉각 용량으로 렌즈의 온도 편차를 줄여서 렌즈의 광학적 성능을 향상시킬 수 있는 적합한 냉각 용량 조건을 도출할 수 있을 것으로 판단하였다.

본 연구는 비구면 렌즈 성형 장비 국산화를 위해 가열, 압축, 냉각 과정에서의 가열 조건과 냉각 조건에 대해 열 해석을 연구하였다. 렌즈의 균일한 온도 분포와 낮은 렌즈 온도 편차의 결과를 바탕으로 렌즈 내 열 응력 발생 가능성과 열 변형 발생에 대해 예측할 수 있음으로, 열 해석의 중요성을 알 수 있다. 이러한 결과를 기반으로 Ansys의 Thermal Transient와 Polyflow 모듈을 활용하여 열-구조 연계 해석을 수행하면, 효율적으로 고품질과 높은 광학 성능을 갖는 비구면 렌즈 성형 조건과 장비 구축이 가능하다고 판단된다.

4. 결론

본 연구에서는 비구면 렌즈 성형 공정(GMP)에서 가열시스템의 열량에 따른 가열/압축/냉각 과정의 렌즈 온도 분포 및 편차에 대해 열 해석을 수행하여 다음과 같은 결론을 도출하였다.

(1) 유리 렌즈를 가열 및 유지하는 Steps 1, 2 과정에서는 6.35 / 2.50 kW, 6.50 / 2.70 kW 가열 조건에서 렌즈 온도가 전이 온도 이상으로 분포하는 것을 분석하였으며, 가소성을 고려하여 6.35 / 2.50 kW가 적합한 것으로 도출하였다.

(2) 압축 과정 Step 3에서는 렌즈 온도는 2.03 kW 가열 열량이 렌즈 온도를 적합하게 유지하는 것으로 분석하였으며, 자연 냉각 Step 4에서 렌즈의 온도 편차도 2°C 이내로 적은 것으로 도출하였다.

(3) 냉각 단계 Steps 5, 6에서는 전도 냉각 방식인 경우, 초기단계에서는 낮은 냉각 용량과 마지막 단계에서는 높은 냉각 용량으로 냉각하는 것이 렌즈의 온도 편차를 감소시켜서 렌즈의 품질 및 광학 성능에 효과적일 것으로 도출하였다.

본 연구에서 가열시스템 열량과 냉각 용량에 대해 열 해석으로 렌즈의 온도 분포 및 편차의 결과 분석을 하였다. 그에 따라 향상된 양산성, 품질, 광학 성능을 갖는 비구면 렌즈 생산이 가능한 국산화 비구면 렌즈 성형 장비를 구축하는 것에 대해 본 연구의 결과가 효율성이 있다고 제안한다.

Acknowledgments

본 논문은 중소벤처기업부에서 지원하는 2022년도 맞춤형기술파트너지원(00166367)과 산학연 플랫폼 협력 기술개발사업(S3310960)의 연구수행으로 인한 결과물임을 밝힙니다.

References

• Seo, B., Jung, D., Park, K., Park, C., (2022), A study on the heat transfer characteristics of a glass lens mold heating block according to design of a heat radiating block, Journal of the Korean Society for Precision Engineering, 39(7), 493-500. [https://doi.org/10.7736/JKSPE.022.058]
• Kwak, D., Chung, W., Kim, E., Jung, D., Kim, W., (2023), Forming conditions of aspherical infrared lens in compression mold forming, Journal of the Korean Society of Manufacturing Process Engineers, 22(2), 1-8. [https://doi.org/10.14775/ksmpe.2022.22.02.001]
• Lee, Y.-M., Chang, S.-H., Heo, Y.-M., Shin, K.-H., Yoon, G.-S., Jung, T.-S., (2008), Thermal stress analysis for an aspheric glass lens mold, Journal of the Korean Society for Precision Engineering, 25(12), 125-131.
• Jung, T.-S., Park, K.-S., Yoon, G.-S., (2011), A study on the optimal molding conditions for aspheric glass lenses in progressive GMP, Journal of the Korea Academia-Industrial Cooperation Society, 12(3), 1051-1057. [https://doi.org/10.5762/KAIS.2011.12.3.1051]
• Ryu, S., Roh, K. H., Choi, K. H., Kim, W. G., Lee, W. K., Kim, D. H., Yang, K. H., (2018), A study on the molding process of an optical communication aspherical glass lens using the weight molding method, Ceramist, 21(4), 427-432. [https://doi.org/10.31613/ceramist.2018.21.4.01]
• Kim, J.-K., Choi, Y.-S., Ahn, J.-H., Son, B.-R., Hwang, Y.-K., (2020), Compression molding of diffractive-aspheric lenses using chalcogenide glasses, Journal of the Korean Society of Manufacturing Process Engineers, 19(6), 43-48. [https://doi.org/10.14775/ksmpe.2020.19.06.043]
• Son, B.-R., Ahn, J.-H., Lee, Y.-H., Hwang, Y.-K., (2021), Optimization of heating conditions for compression molding of chalcogenide glass lenses based on surface defects, Journal of the Korean Society of Manufacturing Process Engineers, 20(8), 60-66. [https://doi.org/10.14775/ksmpe.2021.20.08.0060]
• Dambon, O., Wang, F., Klocke, F., Pongs, G., Bresseler, B., Chen, Y., Yi, A. Y., (2009), Efficient mold manufacturing for precision glass molding, Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena, 27(3), 1445-1449. [https://doi.org/10.1116/1.3056171]
• Yan, J., Zhou, T., Masuda, J., Kuriyagawa, T., (2009), Modeling high-temperature glass molding process by coupling heat transfer and viscous deformation analysis, Precision Engineering, 33(2), 150-159. [https://doi.org/10.1016/j.precisioneng.2008.05.005]
• Yao, H., Lv, K., Zhang, J., Wang, H., Xie, X., Zhu, X., Deng, J., Zhuo, S., (2019), Effect of elastic modulus on the accuracy of the finite element method in simulating precision glass molding, Materials, 12(22), 3788. [https://doi.org/10.3390/ma12223788]
• Shu, C., Yin, S., Li, Y., Mao, Z., Guo, X., Huang, S., (2022), High-precision molding simulation prediction of glass lens profile for a new lanthanide optical glass, Ceramics International, 48(11), 15800-15810. [https://doi.org/10.1016/j.ceramint.2022.02.118]
• Hu, Y., Shen, L., Zhou, J., Li, M., (2018), Numerical study of temperature distribution control in precision glass molding furnace, International Journal of Precision Engineering and Manufacturing, 19, 829-835. [https://doi.org/10.1007/s12541-018-0099-7]