정렬형 접힌 빔 유연기구 기반 팁-틸트-피스톤 정렬기구의 기생운동 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study introduces a novel tip-tilt-piston aligner based on aligned folded beam flexure. It was designed to enhance precision positioning by minimizing parasitic motion. Through finite element analysis, we compared this aligner with a traditional folded beam flexure-based mechanism, revealing a remarkable 135% increase in translational stiffness and superior rotational stiffness ratios. These advancements are expected to reduce parasitic motion arising from actuator misalignment and external disturbances, ultimately elevating positioning accuracy. The aligner’s suitability as a guiding device was affirmed and optimal actuator placement positions were determined. This research provides valuable insights into precision positioning mechanism design, underscoring the role of flexure geometry and precise actuator placement in minimizing parasitic motion for improved accuracy.
Keywords:
Tip-tilt-piston aligner, Aligned folded beam flexure, Parasitic motion, Stiffness analysis키워드:
팁-틸트-피스톤 정렬기구, 정렬형 접힌 빔 유연기구, 기생운동, 강성해석1. 서론
팁-틸트-피스톤(Tip-tilt-piston, TTP) 정렬기구는 2개 회전(팁-틸트)과 1개 병진(피스톤)을 포함한 3개의 면외 자유도(Degree of Freedom, DoF)를 통해 대상물의 위치 결정 및 정렬을 수행한다. 이러한 3자유도 정렬기구는 반도체 제조 장비 등 다양한 산업 분야에서 정밀측정 및 가공 공정을 위한 대상체의 정밀 조작 및 정렬에 적용될 수 있다[1-3]. 전통적인 위치결정 장치에서 사용하는 베어링 등의 접촉식 가이드는 마찰과 백래시를 유발하여 나노미터 수준의 초정밀 공정에 부적합하다. 이들의 대안으로 재료의 탄성 변형을 통해 동작을 안내하고 힘을 전달하는 유연기구가 제안되었다[4]. 유연기구는 이론적으로 원자 규모의 정밀도를 가질 수 있으며 부드럽고 지속적인 움직임이 가능하다. 또한 마찰과 백래시가 없으며 분진이 발생하지 않고, 윤활이 필요 없으므로 클린룸에서 사용 가능한 장점을 갖는다. 따라서 나노미터 수준의 초정밀 위치결정 공정에 유연기구가 일반적으로 사용되고 있다[5]. 그러나 유연기구는 그 구조적 특성으로 운동의 안내와 구속이 동일한 유연기구에 의해 구현되므로 원하는 운동 방향 대비 원하지 않는 구속 방향의 강성비가 유한하며, 접촉식 가이드에 비해 그 값이 상대적으로 낮은 수준이다[6]. 따라서 기생운동을 저감하기 위해서는 유연기구의 기하학적 구조 및 설계 변수를 변경하여 강성비를 최대화하는 노력이 필요하다[7].
초정밀 위치 결정이 요구되는 대표적인 공정의 한 예로 W2W (Wafer to Wafer) 접합 등은 접합 공정을 위해 마주하는 웨이퍼 간의 정렬이 매우 중요하며 오정렬은 수율 저하를 유발한다[8,9]. 따라서 웨이퍼 접합 시 압력과 고하중의 웨이퍼 척 무게를 견디며 팁-틸트-피스톤 운동을 가이드하는 접힌 빔(Folded Beam, FB) 유연기구 기반 웨이퍼 정렬기구가 개발되었다[10].
본 연구는 기존의 팁-틸트-피스톤 정렬기구의 접힌 빔 유연기구 구조를 개선하여 팁-틸트 방향의 회전 강성을 유지하면서 피스톤 방향의 병진 이동 수행 시 기생운동을 저감할 수 있도록, 새로운 정렬형 접힌 빔(Aligned Folded Beam, AFB) 유연기구 기반 팁-틸트-피스톤 정렬기구를 제안한다. 제안된 정렬형 접힌 빔 유연기구 기반 정렬기구의 강성은 유한요소해석(Finite Element Analysis, FEA) 시뮬레이션에서 검증되었으며 기존의 접힌 빔 유연기구 기반 정렬기구와 비교하여 결과를 분석하였다. 기생운동을 저감하기 위한 강성비의 최대화를 위해 구동기의 설치 위치 및 오정렬이 정렬기구의 정밀도에 미치는 영향을 분석하였으며 기생운동 없이 순수한 Z축 병진 이동을 달성하는 최적의 구동기 설치 위치를 분석하였다.
2. 방법
2.1 정렬기구의 구성
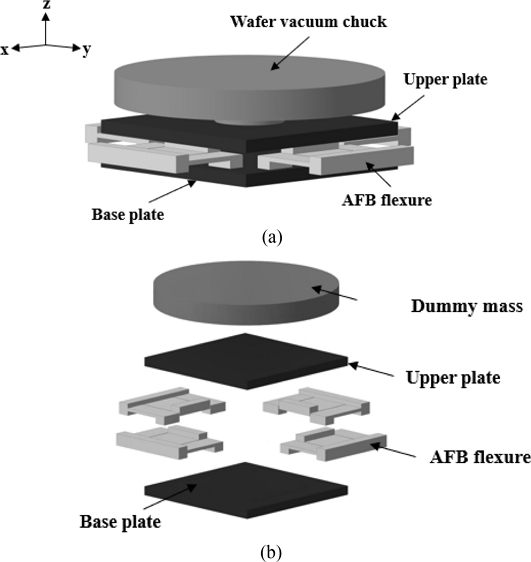
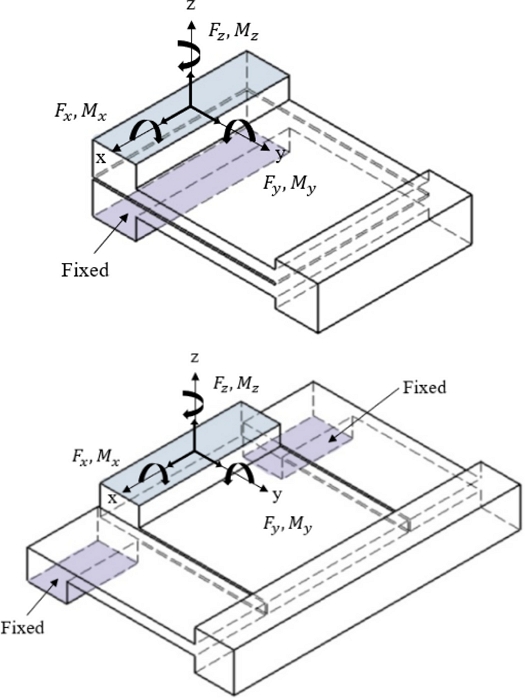
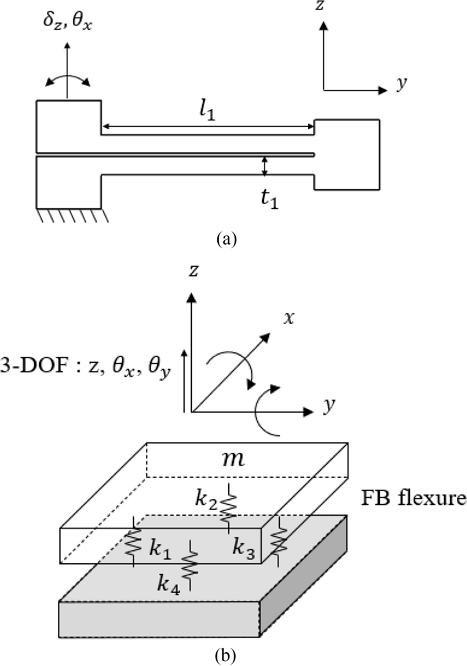
TTP 정렬기구의 구성은 Fig. 1과 같으며 4개의 구동기와 4개의 유연기구를 통해 3자유도(θx, θy, z) 운동을 달성한다. Fig. 1(a)에 제안하는 AFB 유연기구가 도시되어 있으며, 기존의 TTP 정렬기구는 구성요소가 모두 동일하나 유연기구들이 FB 기반이다. Fig. 1(b)는 정렬기구의 분해도를 나타낸다. 정의한 좌표계에 따라 팁-틸트 운동은 X 및 Y축을 중심으로 하는 회전이며, 병진 운동은 Z축 방향을 따른다. 웨이퍼 레벨의 위치 결정 및 정렬을 수행하기 위해 웨이퍼를 고정하는 척(Wafer Vacuum Chuck)이 포함되어야 하며 본 논문에서의 분석을 위해서는 척을 유사한 관성을 가진 단순한 더미(Dummy)로 가정하여 고려하였다. 또한 척을 지지하는 상판(Upper Plate)과 유연기구를 고정하는 베이스판(Based Plate)이 있으며 4개의 유연기구가 이들 두 판 사이에 대칭적으로 배치되어 원하는 운동을 안내한다. 이때 유연기구는 상판 및 베이스판의 둘레를 따라 배치된다. 이는 웨이퍼 간 접합 공정 등을 구현하기 위하여 웨이퍼가 위치한 중심부에 공정 작업용 프로브 등이 배치될 수 있도록 비워 두어야 하기 때문이다. 이에 따라 유연기구 또한 외곽으로 밀려나기 때문에 전체 시스템의 부피 감소를 위해 상판에 포함된 막(Diaphragm) 형태의 유연기구가 아닌 적층 형태의 유연기구가 상판 아래에 구성되었다.
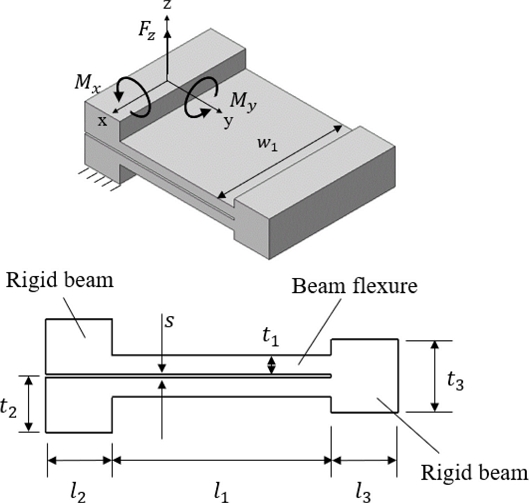
기존의 FB 유연기구[10]는 Fig. 2와 같이 직사각형 단면을 갖는 두 개의 동일한 유연 빔(Beam Flexure)과 이들 빔 사이 또는 상판 및 베이스판과의 연결부에 위치하는 강체 빔(Rigid Beam)으로 구성되어 있다. 상대적으로 두께가 얇은 유연 빔의 변형을 통해 원하는 운동 방향의 자유도를 구현하므로, X축 중심의 굽힘을 통한 회전 및 Z축 병진 방향 변형을 주로 활용한다. 그 외 방향은 높은 강성을 유지하여 기생운동을 구속한다. 정렬기구에서 유연기구를 대칭으로 배치했을 때 더 넓은 운동 범위를 갖기 위해 유연 빔은 폭(w1)보다 상대적으로 긴 길이(l1) 및 얇은 두께(t1)를 가져 X축 중심 굽힘에 의한 변형이 주된 역할을 하도록 설계되었다.
FB 유연기구의 빔 사이 간격(s)은 정렬기구의 목표인 3자유도 면외 동작(θx, θy, z) 시 X 및 Y축 방향 병진 이동 등 원하지 않는 기생운동을 유발할 수 있는 잠재적 원인이 된다. 기생운동 방향으로 인가되는 구동기의 힘 또는 외란에 대해 빔에서 발생할 수 있는 굽힘 모멘트의 팔 역할을 하기 때문이다. 이에 대한 자세한 설명은 보조자료에 나타내었다. 두 유연 빔 사이의 간격을 최소화하여 기생운동을 저감할 수 있으나 FB 유연기구의 구조상 간격을 완전히 제거할 수는 없다. TTP 정렬기구의 운동 범위 내에서 발생하는 FB 유연기구의 변형으로 두 유연 빔이 접촉하지 않아야 하기 때문이다. 따라서 기존의 FB 유연기구 및 이를 활용한 TTP 정렬기구는 시스템 정밀도 달성에 한계를 가지고 있다.
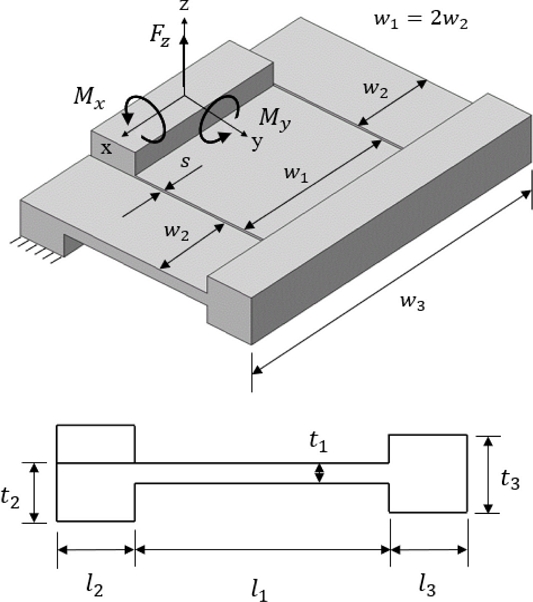
본 연구에서는 TTP 정렬기구의 운동 범위를 유지하면서 피스톤 운동 수행 시 기생운동을 저감할 수 있는 방안을 제시한다. 이는 기존의 FB 유연기구에서 간단한 형상 변화만으로 구현하는 새로운 AFB 유연기구를 이용하여 달성할 수 있다. Fig. 3과 같이 기존의 FB 유연기구의 두 유연 빔 요소 중 하나를 절반으로 나누어 다른 유연 빔 요소의 좌우에 배치한 형태로서 유연 빔들이 정렬된 구조이다. AFB 유연기구 구조는 FB 유연기구에서 유연 빔 사이 간격을 없앤 구조로서 기생운동 방향의 구속 강성이 향상되어 전체 정렬기구의 시스템 정밀도를 향상시키며 기존의 FB 유연기구보다 높이가 작다는 장점을 가진다. 또한 FB 유연기구 대비 폭이 2배 증가하였으나 동일한 길이를 가지므로 웨이퍼 접합 등의 공정 시 장비 중심부의 공간 활용 측면에 저해되지 않는 구조적 장점을 가진다.
유연기구의 강성은 기하학적 매개변수에 크게 영향을 받으며 원하지 않는 방향의 강성을 최대화하고, 원하는 방향의 강성을 최소화하여 목표운동을 안내한다. 따라서 원하는 방향의 낮은 강성을 위해 유연 빔과 같은 탄성 요소의 기하학적 매개변수는 더 긴 길이, 더 작은 폭과 두께를 갖는다. 그러나 이러한 매개변수는 웨이퍼 접합 시 압력과 고하중의 웨이퍼 척 무게를 견디기 어려우며 고유진동수를 감소시킨다. 고유진동수의 감소는 제어 시 공진을 발생시킬 수 있으므로 TTP 정렬기구의 목표 제어주파수인 50 Hz보다 2배 높은 100 Hz를 정렬기구의 최소 고유진동수 목표로 임의 설정하였다.
TTP 정렬기구는 3자유도 면외 동작(θx, θy, z)을 수행해야 하므로 이들 운동과 동일한 구조 모드가 낮은 대역에서 나타난다. X 및 Y축은 대칭성에 의해 동일한 고유진동수가 나타나므로, 피스톤 운동과 팁-틸트 운동 중 낮은 고유진동수가 최소 고유진동수가 된다. 이들 고유진동수는 식(1) 및 식(2)와 같이 등가 관성 및 등가 강성을 통해 구할 수 있다. TTP 정렬기구에서 유연기구의 질량은 상대적으로 매우 작으므로, 등가 관성은 상판 및 척의 질량 및 회전 관성으로 구할 수 있다. 반대로 TTP 정렬기구의 운동 시 대부분의 변형은 유연기구에서 발생하므로, 등가 강성은 각 유연기구의 변형에 따른 거동으로부터 구할 수 있다. 이때, 정렬기구가 피스톤 또는 팁-틸트 운동을 수행할 시 각각의 유연기구가 어떠한 형태로 변형하는지에 따라 적절한 유연기구의 강성을 구하여 정렬기구 전체의 등가 강성으로 변환해야 한다. 각 유연기구의 강성과 전체 정렬기구 등가 강성 간의 관계는 FB 유연기구를 기반으로 구하였으며 이를 보조자료에 나타내었다.
| (1) |
| (2) |
2.2 유한요소해석 기반 분석
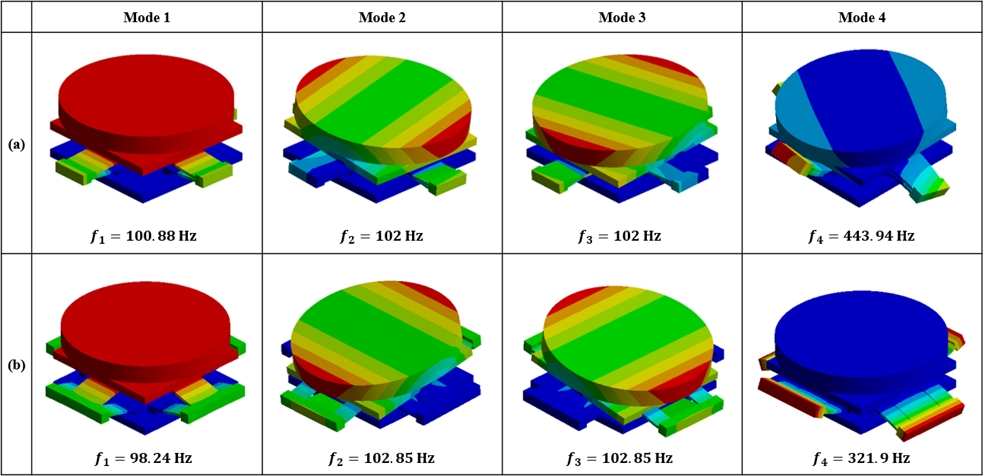
본 연구에서는 새로운 정렬기구의 성능을 분석하는데 FEA (ANSYS, Static Structural, US) 방법론을 이용하였다. 여기에는 제안된 정렬기구와 기존 정렬기구 간의 포괄적인 비교 분석을 포함한다. 이를 위해, 모델 기반 설계를 통해 100 Hz의 고유진동수를 갖는 TTP 정렬기구를 기준으로 FB 유연기구를 설계를 한 후, AFB 유연기구는 FB 유연기구와 동일 형상부에 대해서 기하학적 매개 변수를 동일하게 유지하여 설계하였다. 설계 결과인 기하학적 매개변수는 Table 1과 같다. 두 정렬기구의 고유진동수 비교 결과는 Fig. 4와 같다. 유연기구, 상판, 베이스판의 소재는 Al7075-T6이 사용되었으며 물성은 탄성계수 71.7 GPa, 전단계수 26.9 GPa, 포아송 비 0.33, 밀도 2,810 kg/m3이다.
웨이퍼 진공 척의 재질은 가장 널리 사용하는 Al6061-T6이며 물성은 탄성계수 69 GPa, 전단계수 25.9 GPa, 포아송비 0.33, 밀도 2,713 kg/m3이다.
본 연구에서는 FEA를 통해 기존 정렬기구 대비 새로운 정렬기구의 기생 운동 감소를 병진 및 회전 강성 측면에서 달성한 개선사항을 정량적으로 평가하는 것을 목표로 한다. 따라서 유연기구 단위에서 제안된 유연기구의 기생 운동 저감 효과와 전체 정렬기구 단위에서 강성해석을 통해 기생 운동 저감 효과를 분석하였다.
TTP 정렬기구는 중공을 유지하면서 외곽으로 부피 증대를 막기 위해 상판 아래 적층 형태로 유연기구를 배치하였으므로 상하 비대칭 구조이다. 막 형태의 유연기구 배치는 상하 대칭구조의 구현으로 유연기구의 중심 위치와 구동력의 작용점을 일치시키는 것만으로 충분하다. 그러나 상하 비대칭 구조의 정렬기구는 구동기 설치 위치에 따른 기생운동 발생을 피하기 위해 설계 단계에서 기생운동의 구속력이 높은 최적의 구동력 작용점, 즉 구동기 설치 위치를 판단해야 한다. 따라서 기생 운동을 최소화하고 정밀 위치결정 성능을 향상시키기 위해 구동기 설치 위치에 따른 기생 운동 분석을 같이 수행하였다.
제안된 AFB 유연기구는 정렬기구의 높이를 낮추어 기생운동 강성을 높일 수 있는 구조로 FB 유연기구 대비 기생운동이 저감된 구조이다. 이를 TTP 정렬기구에서 비교하기 전에 유연기구 단위에서 기생운동 구속 효과를 FEA 시뮬레이션을 통해 비교 분석하였다.
유연기구의 상단부(자유단)는 3개의 병진 및 3개의 회전 방향으로 여러 가지 형태의 외력이 인가될 수 있다. 따라서 6축 방향의 하중에 대한 6축 방향 변형량을 시뮬레이션으로부터 도출하여 유연기구의 6자유도 강성행렬(K)을 식(3)과 같이 도출하였다. 시뮬레이션 해석 조건은 Fig. 5와 같이, 각 유연기구의 하단부를 고정하고, 상단부의 윗면에 6축의 단위 하중(F = 1 N, M = 1 Nm)을 인가하였다.
| (3) |
6자유도 하중(U)의 구성 요소는 각각 X, Y 및 Z축을 따라 세 가지 힘과 세 가지 모멘트로 이루어지며 식(4)과 같다.
| (4) |
변형량 벡터(δ)의 성분은 X, Y 및 Z축의 직선 변위와 회전 변위 항으로 구성되며 식(5)와 같다.
| (5) |
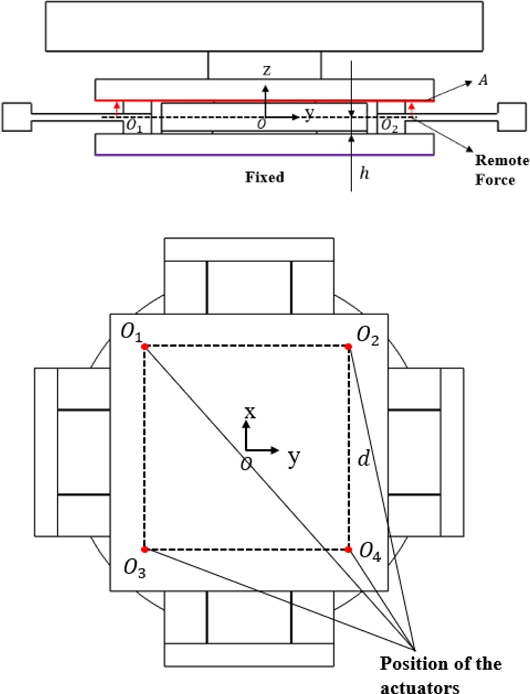
제안된 TTP 정렬기구의 기생운동 구속 효과를 분석하기 위해 FEA 시뮬레이션을 통해 정렬기구 전체에 대한 강성 행렬을 도출하였다. 일반적으로 TTP 정렬기구는 압전소자 또는 보이스 코일 모터와 같은 선형 구동기를 다수 개 이용하여 웨이퍼 정렬을 위한 운동을 수행한다[11]. 정렬기구 단위 해석에서 구동기의 힘을 ANSYS의 원격 힘(Remote Force) 조건을 활용하여 해석을 수행하였으며 원격 힘의 지점(Remote Force Point)은 구동기의 체결 부분으로 식별된다. 시뮬레이션에서 원격 힘을 사용하면 상판에 실제로 구동기와 체결된 본체를 모델링할 필요 없이 상판에 가해지는 힘을 모방할 수 있다. 제안하는 정렬기구에서 구동기는 대칭성을 고려하여 Fig. 6과 같이 4개를 배치하는 것으로 가정하였고, 이는 유연기구의 대칭적 배치와 동일하다. 시뮬레이션에서 이들 구동력은 4개의 원격 힘을 사용하여 정의되었다. 원격 힘은 원격 지점에서 힘이 적용되는 영역으로 원격 노드가 배치되어 다점 연결을 통해 힘이 균일하게 분산된다. 이를 통해 좁은 영역에 작용하는 구동력에 의한 국부적인 변형 등의 효과를 제거하고 유연기구에 따른 기생운동 구속 효과를 비교할 수 있다. 하중은 원격 힘을 이용하여 유연기구의 중심 높이(h) 상의 네 원격 지점(O1, O2, O3, O4)에서 힘이 작용하는 부분인 상판 밑면(A)에 등가 하중이 6축의 단위 하중(F = 1 N, M = 1 Nm)이 되도록 인가하였다. 유연기구의 중심 높이는 상판과 베이스판 사이의 거리의 절반으로 h = 11.9 mm이다. 또한 각각의 힘 인가 지점 사이의 거리 d = 200 mm이다. 정렬기구의 변위는 위치결정 대상체가 놓이는 척 윗면의 중앙점 변위 및 회전을 측정하였다. 베이스판의 밑면은 모든 자유도가 변위가 0 mm, 0 rad로 고정되었다.
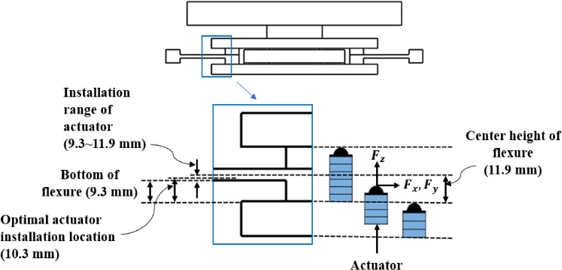
유연기구의 동작에 대한 수학적 모델링은 단일 몸체 구조 및 운동 자유도 증가에 따라 매우 복잡하고, 높은 정확도의 예측이 어렵다[12]. 따라서 FEA 시뮬레이션을 이용한 다자유도 강성해석을 통해 구동기 설치 위치에 따른 기생운동 구속 효과를 분석하였다. 원격 힘 조건을 활용하여 Fig. 7과 같이 구동력의 작용점 높이를 변경하여 원하는 운동 방향과 기생운동 방향의 강성을 비교하였다. 구동기 설치 위치의 변화에 해당하는 구동력 작용점의 변화 정도는 구동기 조립 시 활용할 수 있는 부품의 일반적인 제작 공차 및 예압 스크루를 이용한 위치 조정을 고려하여 100 μm로 설정하였다.
3. 결과
3.1 기생 운동 감소 효과
강성 행렬(K)의 성분은 식(3)의 평형방정식을 기반으로 변형량 및 하중 벡터의 관계로 인해 6 × 6 정방 행렬로 나타나며 Table 2는 AFB 유연기구와 FB 유연기구의 강성 행렬 중 대각성분을 비교한 표이다. 대각 성분은 동일한 방향의 하중과 변형량 사이의 관계를 나타낸다. 2.1.1절에서 언급했던 바와 같이 1개의 유연기구는 Z축을 따라 병진 운동과 X축 중심의 회전을 포함한 2자유도를 갖는다. 그 외 4자유도 방향의 강성은 기생운동 강성으로 볼 수 있다. 이를 Table 2의 방향별 강성 값의 차이로부터 확인할 수 있다. 또한 AFB 유연기구의 기생운동 강성이 FB 유연기구 대비 모두 증가함을 볼 수 있다. 이는 AFB 유연기구가 FB 유연기구 대비 기생운동을 저감할 수 있는 구조임을 보여준다. 또한 제안된 TTP 정렬기구에 대해 기존 정렬기구 대비 기생 운동 저감 효과를 확인하기 위해서 정렬기구 단위에서 기생 운동 분석을 수행하였다.
3.2 병진 및 회전 강성비
Tables 3과 4는 FEA 시뮬레이션을 통해 도출된 각각의 FB 유연기구 기반 정렬기구와 AFB 유연기구 기반 정렬기구의 6 × 6 강성행렬을 나타낸 표이다. 각 성분의 단위는 행의 힘 또는 모멘트를 열의 선형 변위 또는 각도로 나눈 값의 단위이다. 정밀 위치 결정 시스템은 원하는 운동 방향의 강성 대비 원하지 않는 운동 방향 강성의 차이를 증가시켜 다자유도 운동 수행 시 기생 운동을 최소화한다. 해석 결과에서 이러한 강성의 차이를 비교를 위해 식(6)과 식(7)과 같이 병진운동 강성비(ru) 및 회전운동 강성비(rθ)를 정의한다. Table 5는 FB 유연기구 기반 정렬기구와 AFB 유연기구 기반 정렬기구의 병진 운동 및 회전 운동 방향의 강성비를 나타낸 표이다.
| (6) |
| (7) |
제안된 AFB 유연기구 기반 정렬기구는 FB 유연기구 기반 정렬기구 대비 병진운동 강성비가 135%로 2배 이상 크게 증가하였다. 이로부터 새롭게 제안한 AFB 유연기구가 정렬기구에서 기생운동 구속 효과가 매우 뛰어남을 확인할 수 있다. 그러나 상대적으로 회전운동 강성비는 13% 감소하였다.
3.3 구동기 설치 위치에 따른 기생운동 분석
Figs. 8과 9는 각각 FB 및 AFB 유연기구 기반 정렬기구의 구동기 설치 위치에 따른 6자유도 강성 변화를 나타낸다. Figs. 8(a)와 9(a)는 100 μm의 구동기 설치 위치의 제어 정도에 대한 병진운동 강성의 변화를 나타낸다. 두 정렬기구 모두 100 μm의 작은 구동기 설치 위치의 변화에도 병진 운동 강성비가 각각 최대 34.2, 28.9배 차이가 났다. 이러한 결과는 구동기 설치 위치가 TTP 정렬기구의 기생 운동 구속에 큰 영향을 미치며 기생운동을 최소화할 수 있는 최적의 구동기 설치 위치가 있음을 보여준다.
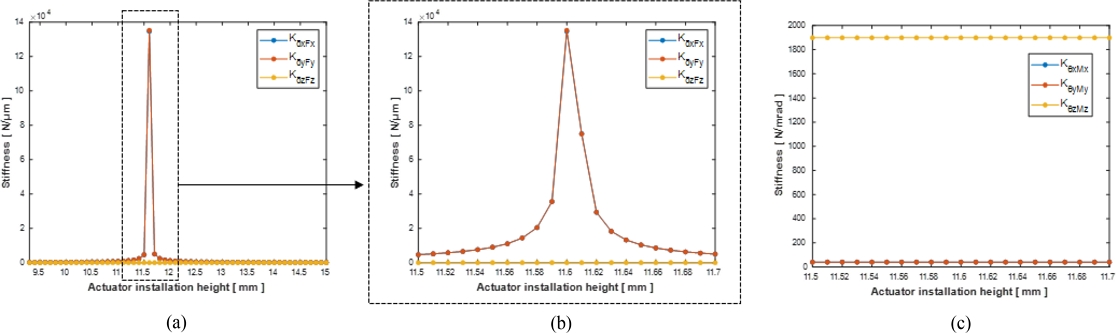
Stiffness variation due to the actuator installation position of the FB flexure-based aligner. (a) Stiffness in the direction of translational motion. (b) Enlarged view of (a). (c) Stiffness in the direction of rotational motion
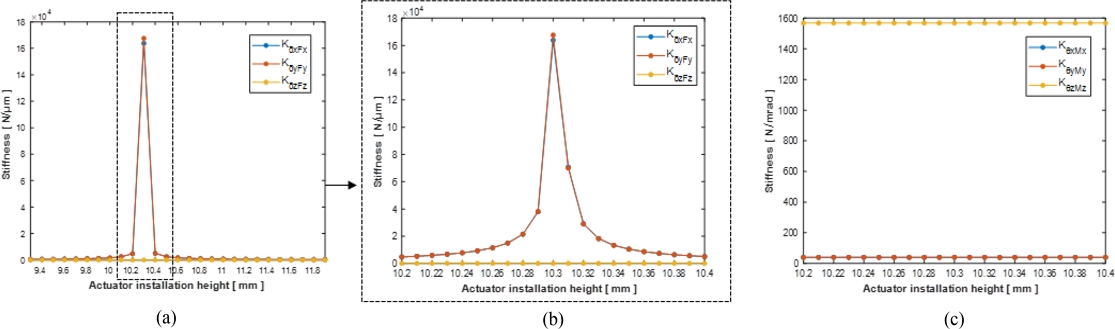
Stiffness variation due to the actuator installation position of the AFB flexure-based aligner. (a) Stiffness in the direction of translational motion. (b) Enlarged view of (a). (c) Stiffness in the direction of rotational motion
Figs. 8(b)와 9(b)는 10 μm의 구동기 설치 위치의 제어 정도에 따른 병진운동 강성비의 변화를 나타낸다. 강성이 증가한 근접 부근 내의 더 작은 단위에서도 유사한 경향이 나타나는 것을 보여주며, 이로써 급격한 강성 증가에 대한 데이터의 신뢰성을 확인할 수 있다. Figs. 8(c)와 9(c)는 구동기 설치 위치의 정도에 따른 회전 운동 강성비를 나타낸다. 각각의 결과에서 z축 병진 운동 강성과 회전 운동 강성은 구동기 설치 높이의 변화와 상관없으므로 일정하게 유지된다.
Table 6 은 최적의 구동력 인가 위치에서 FB 및 AFB 유연기구 기반 정렬기구의 6자유도 강성을 비교한 표이다. 최적의 구동력 인가 위치는 FB 및 AFB 유연기구 기반 정렬기구에 대해 각각 h = 11.6 mm 및 h = 10.3 mm이다. 최적의 구동기 설치 위치에서 AFB 유연기구 기반 정렬기구가 FB 유연기구 기반 정렬기구 대비 기생운동 방향으로 더 큰 강성을 갖는다. 또한 Table 6을 Tables 3과 4와 비교하였을 때, 최적의 구동기 설치 위치에서의 병진 운동 강성이 FB 유연기구 기반 정렬기구는 최대 950배, AFB 유연기구는 515배의 큰 폭으로 증가함을 확인하였다. 따라서 구동기 설치 위치에 따른 기생운동 구속 효과의 변화를 확인하였다.
4. 고찰
4.1 정렬기구의 설계
정렬 기구 등 초정밀 위치 결정장치에서 가이드 역할을 수행하는 유연기구는 원하는 방향으로의 운동을 제약 없이 안내하고 원하지 않는 방향으로의 운동을 전혀 허용하지 않는 것이 가장 이상적이다. 이러한 특성이 중요한 이유는 (1) 구동기를 사용하여 원하는 방향으로 힘을 인가하였을 때 원하는 방향의 운동만 발생하도록 보장해야 하는 점, (2)구동기가 이상적으로 원하는 방향으로만 힘을 내도록 제작 및 설치하는 것이 불가능함에도 원하는 방향의 운동만 발생하도록 보장해야 하는 점, (3) 구동기 외에도 다양한 형태의 힘들이 외란으로 작용하지만 원하는 방향의 운동만 발생하도록 보장해야 하는 점 등에 기인한다. (1)을 보장하기 위해서는 정렬기구의 강성행렬에서 대각성분의 값이 비대각성분의 값보다 월등히 낮아야 하고, (2)를 보장하기 위해서는 기생운동 방향의 강성이 매우 커야 하며, (3)을 보장하기 위해서는 정적 강성뿐만 아니라 모드 형상에 따른 동적 강성의 확보가 요구된다. 본 연구에서는 정적 강성만을 고려하였으나 유연기구의 유효 질량은 매우 작다는 가정하에 동적 강성은 정적 강성을 따른다고 볼 수 있다. 그러한 측면에서 볼 때, 새롭게 제안한 정렬형 접힌 빔 유연기구는 기존의 접힌 빔 정렬 기구에 대비하여 기생 운동을 효과적으로 제한한다. 또한 구동기 설치 위치의 정밀한 조정을 통해 기생 운동을 극적으로 제한할 수 있음을 입증하였다.
Table 7은 유연기구의 중심 높이에 구동기가 설치된 FB 유연기구 기반 정렬기구(Case 1)와 구동기 설치 위치가 고려된 AFB 유연기구 기반 정렬기구(Case 2)에 대해 6자유도 강성비를 비교한 표이다. Case 1의 강성 값은 Table 3의 대각선 성분에서 찾을 수 있으며, Case 2는 Table 6의 AFB 자료에서 찾을 수 있다. Case 2에서 병진운동 강성비()는 Case 1 대비 1,241배 증가하였다. 이는 AFB 유연기구 기반 정렬기구가 병진운동 방향으로 높은 기생운동 구속력이 있음을 의미한다. 회전운동에 대한 강성비()는 Case 2에서 다소 감소하지만 기존문헌에서 보고된 정렬기구[13]의 강성비와 비교하여 3자유도 면외 운동 수행 시 양호한 성능을 가질 것으로 예상된다. 또한 Cases 1과 2의 목표 운동 방향인 면외 3자유도(θx, θy, z) 방향의 강성은 서로 5% 이하의 차이를 보이며, 이는 정렬기구의 설계 단계에서 유연기구의 기하학적 구조 개선 및 구동기 설치 위치를 고려하여 기존 3자유도 면외 운동의 이동성을 저해하지 않으면서 기생운동 구속을 통해 위치결정 정밀도 향상을 기대할 수 있음을 보여준다.
4.2 강체 가정 설계의 영향
3.2절의 제안된 정렬기구의 회전 강성비가 감소한 이유는 제안된 정렬기구의 Z축 회전 강성이 기존 정렬기구 대비 감소했기 때문이다. 이러한 결과는 유연기구 단위에서 AFB 유연기구가 FB 유연기구보다 Z축 회전 강성이 증가한 것과 반대의 결과이다. AFB와 FB 유연기구는 동일한 치수의 판스프링을 갖고 있으나 구조적 특성상 강체의 크기가 동일하지 않다. 일반적으로 링크-조인트 기구학에 기반한 유연기구 설계에서 강체는 힘이 가해져도 변형이 없는 무한한 강성을 갖는다고 가정한다. 그러나 실제 시스템에서 강체의 변형은 불가피하다. 따라서 단일 유연기구와 달리 고하중의 척과 상판이 결합된 전체 정렬기구 단위에서의 결과 오차가 발생할 수 있다.
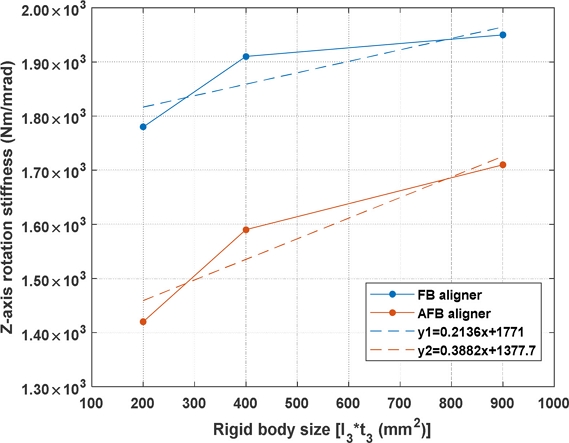
Z축 회전 운동 방향의 감소는 이러한 강체 변형과 관련되어 있으며 두 유연기구에 대해 모든 기하학적 치수는 고정한 뒤 강체의 치수(l3, t3)를 조절하여 전체 정렬기구 단위에서 Z축 회전 강성의 변화를 Fig. 10에 나타냈다. 분석 결과 두 정렬기구는 강체의 크기가 증가할수록 Z축 회전 강성이 증가하였으며 이는 강체의 변형이 성능에 영향을 미침을 나타낸다. 각각의 회전 운동 강성의 데이터에서 추세선의 기울기는 AFB 유연기구 기반 정렬기구가 FB 유연기구 기반 정렬기구 대비 1.8배 크다. 따라서 강체의 크기를 증가시켜 변형이 충분히 작아진다면 AFB 유연기구 기반 정렬기구는 FB 유연기구 기반 정렬기구 대비 더 높은 회전 강성비를 가질 것으로 기대된다. 실제 정렬기구의 구현에서 강체로 가정한 부분의 변형이 설계치 대비 오차를 야기하므로 이를 해결할 수 있는 구조적 개선, 생성적 설계, 신소재 적용 등을 고려할 수 있다. 구체적으로, 높은 비강성 소재로 강체부를 보강함으로써 유연기구의 소형화에 기여할 뿐만 아니라 기생 운동을 효율적으로 제한할 수 있을 것이다.
그러나 이러한 회전운동 강성비의 감소에도 불구하고 Table 4에서 AFB 유연기구 기반 정렬기구의 강성이 대각 성분에서 Z축 회전 강성이 그 외 회전 강성 성분보다 100배 이상의 큰 값을 가지며 대각 성분이 비대각 성분보다 최소 100배 이상 작은 것을 볼 수 있다. 이는 방향별로 인가 하중의 방향에 대해 발생 변위의 방향이 일치하며, 인가 하중의 방향과 다른 방향으로의 변위 발생량이 매우 작은 것을 의미한다. 즉 방향별로 하중과 변위의 관계가 분리(Decoupling)되어 있으므로 기생운동 구속 효과가 여전히 유효하다고 볼 수 있다.
5. 결론
본 논문에서는 팁-틸트-피스톤 정렬 기구의 기생운동 구속 효과를 높여 위치결정 성능을 향상시킬 수 있는 새로운 유연기구 기반 웨이퍼 정렬기구를 제안하였다. 이러한 성능 향상은 기존의 FB 유연기구의 빔 사이에 있는 간격을 제거하는 설계 구조를 통해 달성되었다. 제안된 정렬기구의 기생운동 구속 효과를 검증하기 위해 유한요소법을 통해 기존의 FB 유연기구 기반 정렬기구와 제안된 정렬기구의 다자유도 강성 행렬을 비교 분석하였다.
분석 결과 팁-틸트-피스톤 정렬기구에서 정렬된 접힌 빔유연기구의 적용으로 기생운동 구속 효과를 검증하였다. 기존 정렬기구 대비 병진운동 방향의 강성비가 135% 증가하였으며 기존 문헌자료 대비 높은 회전운동 방향 강성비를 나타내었다. 높은 병진 강성비는 구동기 정렬 오차 및 외란 부하로 인한 기생운동을 저감하여 정렬기구의 위치결정 성능을 향상시킬 수 있을 것으로 기대된다. 또한 유연기구의 형상이 변경되었음에도 목표 운동 방향의 3자유도(θx, θy, z)에 해당하는 강성 행렬의 대각요소 값이 유사하고, 방향별 분리성도 유지하여 팁-틸트-피스톤 정렬기구의 안내 장치로서 효용성을 검증하였다.
구동기 설치 위치에 따라 발생하는 기생운동에 대해서도 분석이 이뤄졌으며, 100 μm의 미소한 구동기 위치 변경에도 최대 34.2배의 병진 강성비 차이가 발생하는 것을 확인하여, 기생운동 구속력을 최대화하는 최적의 구동기 설치 위치를 확인 및 도출하였다. 본 연구의 분석 결과는 유연기구의 기하학적 구조 개선과 더불어 구동기 위치의 정교한 결정이 기생운동 구속을 통한 위치결정 정밀도 향상에 기여할 수 있음을 입증하고 있다.
Acknowledgments
이 연구는 서울과학기술대학교 교내연구비의 지원으로 수행되었습니다.
REFERENCES
-
Kim, H. Y., Kim, J. J., Ahn, D. H., Gweon, D. G., (2013), Development of a nanoprecision 3-DOF vertical positioning system with a flexure hinge, IEEE Transactions on Nanotechnology, 12(2), 234-245.
[https://doi.org/10.1109/TNANO.2013.2242088]

-
Chen, G., Ding, Y., Zhu, X., Liu, P., Ding, H., (2019), Design and modeling of a compliant tip-tilt-piston micropositioning stage with a large rotation range, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 233(6), 2001-2014.
[https://doi.org/10.1177/0954406218781401]

-
Hao, G., (2017), Determinate design and analytical analysis of a class of symmetrical flexure guiding mechanisms for linear actuators, Journal of Mechanical Design, 139(1), 012301.
[https://doi.org/10.1115/1.4034579]

-
Shin, H.-P., (2013), Design of a 6-DOF stage for precision positioning and large force generation, Journal of the Korean Society for Precision Engineering, 30(1), 105-112.
[https://doi.org/10.7736/KSPE.2013.30.1.105]

-
Smith, S. T., (2017), Foundations of ultra-precision mechanism design, CRC Press.
[https://doi.org/10.1201/9781315272603]

-
Awtar, S., (2004), Synthesis and analysis of parallel Kinematic XY flexure mechanisms, Ph.D. Thesis, Massachusetts Institute of Technology.
[https://doi.org/10.1115/DETC2005-85413]

-
Lee, H.-J., Kim, H.-C., Kim, H.-Y., Gweon, D.-G., (2013), Optimal design and experiment of a three-axis out-of-plane nano positioning stage using a new compact bridge-type displacement amplifier, Review of Scientific Instruments, 84(11).
[https://doi.org/10.1063/1.4827087]

-
Kim, S. E., Kim, S. (2015), Wafer level Cu-Cu direct bonding for 3D integration, Microelectronic Engineering, 137, 158-163.
[https://doi.org/10.1016/j.mee.2014.12.012]

-
Shin, S. W., Park, M. S., Kim, S. E., Kim, S. D., (2013), Effects of wafer warpage on the misalignment in wafer level stacking process, Journal of the Microelectronics and Packaging Society, 20(3), 71-74.
[https://doi.org/10.6117/kmeps.2013.20.3.071]

- Kim, T. H., Mun, J. W., Choi, Y. M., An, D. H., Lee, H,-J., (2022), Upper wafer handling module design and control for wafer hybrid bonding, Journal of the Semiconductor & Display Technology, 21(1), 142-147.
-
Ghafarian, M., Shirinzadeh, B., Al-Jodah, A., Das, T. K., Pinskier, J., (2020), Fea-based optimization of a complete structure of a monolithic z/tip/tilt micromanipulator, Journal of Micro-bio Robotics, 16(1), 93-110.
[https://doi.org/10.1007/s12213-020-00133-4]

-
Lai, L.-J., Zhu, Z.-N., (2016), Modeling and analysis of a compliance model and rotational precision for a class of remote center compliance mechanisms, Applied Sciences, 6(12), 388.
[https://doi.org/10.3390/app6120388]

-
Teo, T. J., Chen, I. M., Yang, G., (2014), A large deflection and high payload flexure-based parallel manipulator for UV nanoimprint lithography: Part II. Stiffness modeling and performance evaluation, Precision Engineering, 38(4), 872-884.
[https://doi.org/10.1016/j.precisioneng.2014.04.012]

-
Smith, S. T., (2000), Flexures: Elements of elastic mechanisms, CRC Press.
[https://doi.org/10.1201/9781482282962]

Appendix
APPENDIX
A1. 강성 모델링
본 장에서는 간단한 수학적 모델링을 통해 단일 유연기구단위의 강성을 구하여 유연기구가 장착된 전체 정렬기구의 등가 강성을 유도한다. Fig. 1은 FB 유연기구의 2자유도 운동과 각각의 유연기구를 단순하게 스프링으로 치환하여 정렬기구에 장착된 모델을 나타낸다. FB 유연기구는 유연기구 단위에서 1개의 병진 이동과 1개의 회전을 제공하는 2개의 자유도를 갖으며 Fig. 1(a)에 나타나 있다.
정렬기구에 장착된 개별 유연기구는 각각의 자유도가 결합되어 전체 시스템의 자유도를 결정한다. 따라서 유연기구 단위에서 전체 시스템의 자유도에 주요한 영향을 미치는 Y, Z축 병진운동 강성과 X축 회전 운동 강성에 대해 간단한 외팔보의 처짐식을 응용하여 모델링하였다.
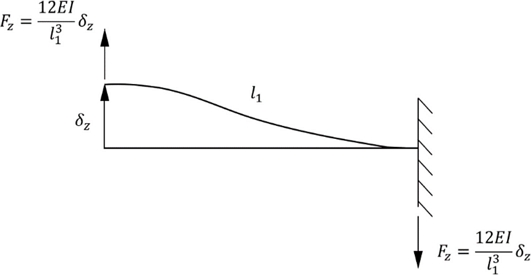
자유 단에 적용된 Z축 병진 이동은 Fig. 2와 같이 각 빔이 ‘s’자로 왜곡되도록 한다. FB 유연기구는 두 빔이 직렬로 연결되어 있기 때문에 각각의 빔은 동일한 힘과 변위를 받는다. 따라서 FB 유연기구의 z축 강성은 각 빔에 대한 강성의 절반으로 식(1)과 같이 나타낼 수 있다. 여기서 kδzFz는 Z축 병진 운동 강성, Fz는 Z축 방향 힘, δz는 Z축 방향 변위, E는 탄성계수, I는 단면적 2차 모멘트이다.
| (1) |
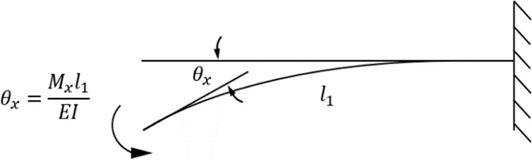
x축에 대한 회전의 경우 각 빔은 전체 FB 유연기구의 변형각의 절반으로 변형하며 Fig. 3과 같이 단순 빔 형태로 구부러진다. 결과적으로 각 처짐을 유도하는데 필요한 굽힘 모멘트는 식 (2)와 같다. 식(2)를 이용하여 도출된 강성 상수를 식(3)에 나타내었다. Mx는 X축 방향 모멘트, θx는 X축 방향 변형각을 의미한다.
| (2) |
| (3) |
FB 유연기구의 Y축 방향 변위는 두 가지 변형 요소로 변위를 제공한다. 첫 번째는 두 빔의 동일한 확장 및 압축이 결합되어 제공되는 변위, 두 번째는 두 빔 사이 간격(s)의 레버 암으로 인한 것이다. 작은 처짐을 가정하면 Y축 방향 변위 강성은 이전 연구 Smith et al.[14]에서 식(4)와 같이 표현할 수 있다. 간단한 분석을 통해 기생 운동인 Y축 병진 운동 강성은 빔 사이 간격을 작게 유지하는 것이 기생 운동을 줄일 수 있음을 보여준다. 여기서 kδzFz는 Y축 병진 운동 강성, Fy는 Y축 방향 힘, δy는 Y축 방향 변위이다.
| (4) |
위와 같이 도출된 유연기구 단위의 강성을 통해 전체 정렬기구의 등가 강성을 도출할 수 있으며 내용은 다음과 같다.
정렬기구 단위에서 4개의 FB 유연기구의 자유단은 상판의 네 모서리에 동일하게 배치되어 있으며 Fig. 1(b)와 같이 질량과 강성 시스템으로 근사화 할 수 있다. 4개의 FB 유연기구의 치수와 재질이 같으므로 FB 유연기구 1개의 강성은 전체 시스템의 강성의 1/4 크기의 강성을 갖으며 식(5)와 같다. ke1은 전체 시스템의 평형 강성 상수를 나타낸다.
| (5) |
| (6) |
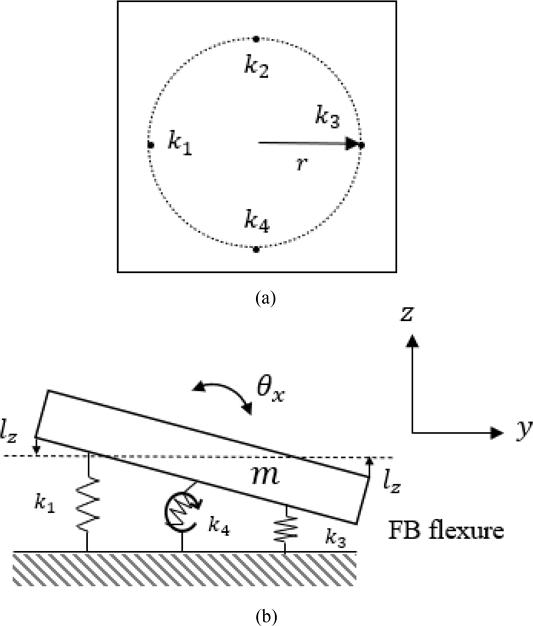
Fig. 4(a)는 각각의 FB 유연기구가 전체 시스템의 중심으로부터 평면상에 거리(r)만큼 떨어져 있음을 보여준다. Fig. 4(b)는 스프링으로 치환된 각각의 유연기구의 운동 조합으로 정렬기구가 X축으로 회전 운동하는 모습을 나타낸다. θx는 X축 방향 변형각을 의미한다
전체 시스템의 X축에 대한 회전 강성은 주요한 두 가지형 요소의 조합으로 변위를 제공한다. 첫 번째는 FB 유연기구의 길이 방향 축을 중심으로 발생되는 비틀림 각 변형과 두 번째는 회전 중심으로부터 평면상에 FB 유연기구가 떨어진 거리만큼의 레버암으로 인한 변위이다.
작은 처짐을 가정하면 전체 시스템의 2개의 유연기구(k2, k4)는 Fig. 4(b)와 같이 비틀림 변형이 발생되고, 나머지 2개(k1, k3)의 변형은 레버암으로 인한 처짐(lz)이 발생되므로 전체 시스템의 회전 모멘트는 식(7)과 같다. 따라서 각 회전 변형을 통해 전체 시스템의 X축 회전 강성은 식(8)과 같이 나타내었다.
Me와 ke2는 각각 등가 굽힘 모멘트와 등가 회전 강성을 나타내며 kt는 비틀림 강성 상수를 나타낸다.
| (7) |
| (8) |
k2, k4의 강성을 갖는 유연기구는 X축에 대한 회전의 경우 각 빔은 전체 FB 유연기구의 변형각의 절반으로 변형하며 단순 빔 형태로 비틀린다. 따라서 2개의 유연기구는 비틀림을 받는 직사각형 단면 빔이 비틀림 각이 절반일 경우의 비틀림 강성으로 근사할 수 있으며 식(9)과 같다. G는 전단계수를 나타낸다.
| (9) |
식(8)에 식(1)과 식 (9)를 대입하면 다음과 같다.
| (10) |
각각의 FB 유연기구 기반 정렬기구의 병진 운동과 회전 운동의 등가 강성은 TTP 정렬기구의 고유진동수를 결정할 수 있다. 병진 운동 등가 강성은 질량 m으로부터 고유진동수를 계산하며, 회전 운동 등가 강성은 관성모멘트를 통해 고유진동수를 계산할 수 있다. 각각의 질량과 관성 모멘트 값은 m = 9.7912 kg, J = 89,343 kgmm2이다. 계산된 고유진동수는 FEA 시뮬레이션(ANSYS, US)을 통해 얻은 고유진동수와 비교되었으며 이를 통해 첫 번째 고유진동수가 100 Hz인 기하학적 설계 변수를 도출하였다.

M.S. candidate in the Department of Mechanical Design and Robot Engineering, Seoul National University of Science and Technology. Her research interest is multi degree of freedom compliance mechanism.
E-mail: yunhyeen1871@gmail.com

Assistant professor of the Department of Mechanical System Design Engineering, Seoul National University of Science and Technology, His research interest is precision motion mechanism.
E-mail: dhahn@seoultech.ac.kr