외란 관측기 기반 자기부상 제어 강화

1. 서론

자기 부상은 물리적 접촉 없이 대상체를 공중에 띄우는 방법으로 비접촉, 조용한 운전, 고효율 등의 장점을 가지고 있다. 자기 부상 기술의 대표적인 적용처로는 운송, 지지 베어링, 물류 등이 있다[1,2]. 특히 능동 자기 베어링(Active Magnetic Bearing, AMB) 회전기계는 에너지와 비용 절감뿐 아니라 크기, 진동 및 소음에서도 뚜렷한 개선이 있다[3].

자기 부상 시스템(Magnetic Levitation System, MLS)은 입력 전압을 통해 코일의 전류를 조절하고 자기력을 발생시켜 물체의 위치를 제어하는 비선형 시스템이다[4]. 전류 제곱에 비례하고 공극 제곱에 반비례하는 비선형 자기력 때문에 평형점의 작은 변화에도 불안정해질 수 있으며 제어 성능이 떨어질 수 있다.

외란 관측기(Disturbance Observer, DOB)는 간단한 구조이지만 모델 불확정성에도 외란을 효과적으로 제거할 수 있다[5-8]. 전압 제어 MLS에 위치 제어에 DOB를 적용하여 외란 제거와 명령 추종 성능을 향상시켰다[9-11]. 전류 제어 MLS의 경우 위치 제어뿐만 아니라 전류 제어에도 DOB 적용이 가능하지만 이에 대한 연구는 진행되지 않았다.

이 논문에서는 MLS의 DOB 기반 제어 강화에 대해 연구했다. PID 위치와 PI 전류 제어를 조합한 전류 제어 MLS가 전압 제어 MLS보다 넓은 제어 설계 자유도와 높은 제어 성능을 가진다. DOB를 PI 전류 제어에 적용하여 쇠공 위치에 따른 인덕턴스 변화를 보상하였고 PID 위치 제어에 DOB를 적용하여 외란 제거 성능을 향상시켰다. DOB 기반 제어 강화의 효과를 정현파 외란 제거, 초기 부상 그리고 폐루프 주파수 응답 측정을 통해 확인하였다. 마지막으로 전류와 위치 DOB의 차단 주파수를 변경시키며 최적화를 수행하였다.

2. 시스템 모델링

2.1 자기부상 시스템

MLS는 대상체(쇠공) 위치를 측정하고 전자석 코일 전류를 전압으로 조절하여 전자기력으로 물체를 부상시키는 비선형 시스템이다[12]. Fig. 1에 실험에서 사용된 MLS와 개략적인 수학적 모델을 나타냈다. u는 전자석 코일 전압, x₁은 쇠공 위치, x₃은 코일 전류, m은 쇠공 질량, g는 중력 가속도이다.

Fig. 1

MLS

2.2 모델링

$\[ \dot{x_1}=x_2 \]$

(1)

$\[ {\dot{x}}_2=-\frac{F_{em}}{m}+g \]$

(2)

$\[ {\dot{x}}_3=\frac{1}{f_i}\left(k_{i}u+c_i-x_3\right) \]$

(3)

$\[ F_{em}=x_3^2\frac{F_{em P1}}{F_{em P2}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{x_1}{F_{em P2}}\right) \]$

(4)

위 식을 평형점(x₁ = 0.01 m)에서 선형화하여 상태공간 모델로 식(5)에 나타냈다. A, B, C는 상태, 입력, 출력 행렬이다. MLS 파라미터는 Table 1에 나타냈다.

$\[ \dot{x}=Ax+Bu,y=Cx \]$

(5)

$$ \begin{array}{c}\mathrm{H}\mathrm{e}\mathrm{r}\mathrm{e},\mathrm{ }A=\left[\begin{array}{ccc}0& 1& 0\\ a_{\mathrm{2,1}}& 0& a_{\mathrm{2,3}}\\ 0& 0& a_{\mathrm{3,3}}\end{array}\right], B=\left[\begin{array}{c}0\\ 0\\ b_3\end{array}\right], C=\left[\begin{array}{c}1\hspace{0.25em}0\hspace{0.25em}0\end{array}\right]\mathrm{ }\hfill \\ a_{\mathrm{2,1}}=\frac{x_{30}^2}{m}\frac{F_{em P1}}{F_{em P2}^2}{e}^{-\frac{x_{10}}{F_{em P2}}},{ a}_{\mathrm{2,3}}=\frac{2x_{30}}{m}\frac{F_{em P1}}{F_{em P2}}{e}^{-\frac{x_{10}}{F_{em P2}}},\\ a_{\mathrm{3,3}}=-f_i^{-1}, \text{and} b_3=k_i{f}_i^{-1}\end{array}$$

Table 1

Parameters of MLS

3. LMS 모델 분석

3.1 극점

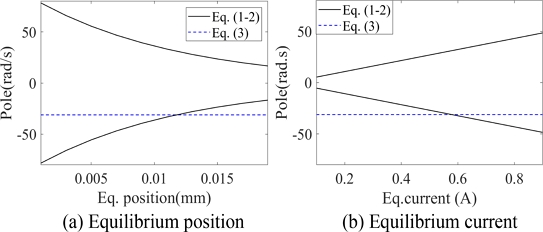
평형 위치와 전류 변화에 따른 극점 위치 변화는 Fig. 2에 나타냈다. Fig. 2(a)는 전류가 0.672 A일 때 평형점 위치 변화에 따른 극점 위치 변화이고, Fig. 2(b)는 평형 전류 변화에 따른 극점 위치 변화이다. 대상체 평형 위치나 전류가 바뀌면 극점 위치가 크게 변하기 때문에 이를 보상하기 위한 제어 강화 기법이 필요하다.

Fig. 2

Pole movement due to equilibrium changes

3.2 전류 제어 MLS

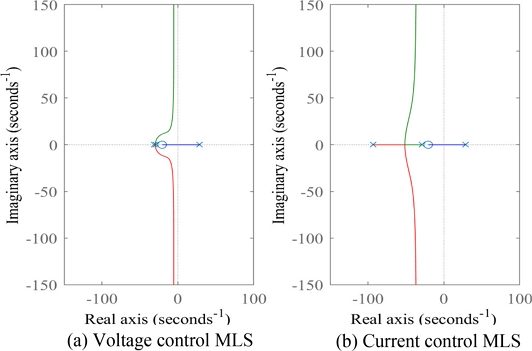
전압과 전류 제어 MLS에 PD 위치 제어를 적용한 근궤적 선도를 Fig. 3에 나타냈다. 전류 제어 MLS는 PI 전류 제어가 포함되어 있다. 전압 제어 MLS는 Fig. 3(a)와 같이 PD 제어 영점이 극점에 접근함에 따라 시스템은 빨라지지만 감쇠가 적은 공액 극점을 갖는다. 반면, 전류 제어 MLS는 Fig. 3(b)와 같이 PI 전류 제어로 전기 시스템(식(3)) 극점이 원점에서 멀어지고 충분한 감쇠를 갖는 공액 극점을 갖는다. 이 논문은 제어 이득 조절 범위가 넓고 제어 성능을 높일 수 있는 전류 제어 MLS를 연구대상으로 하였다.

Fig. 3

Root locus of voltage and current control MLS with PD position control

4. 전류 제어 MLS

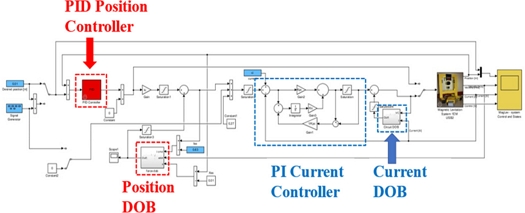
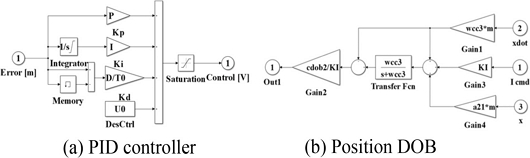
전류제어 MLS 실시간 시뮬링크 블록선도를 Fig. 4에 나타냈으며, PI 전류 제어, PID 위치 제어, 전류 및 위치 DOB로 구성된다.

Fig. 4

The current controlled MLS control system

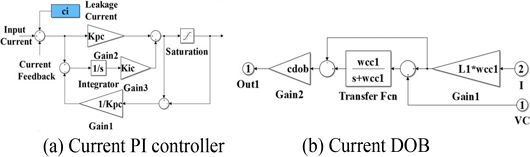
PI 전류 제어기와 전류 DOB 구조를 Fig. 5에 나타냈다. Kpc와 Kic는 전류 제어 비례와 적분 이득이며 제어 출력 제한과 안티와인드업(Anti-windup) 제어를 포함한다. PI 전류 제어 이득은 제어 주기, 전자석 코일 공칭 인덕턴스와 저항을 고려하여 선정하였다. 전류 DOB는 전압과 전류의 일차 미분 방정식을 이용하여 구현하였으며 코일 저항(R), 인덕턴스(L1) 그리고 1차 저역 통과 필터(차단 주파수 wcc1)로 구성된다. 저역 통과 필터 대역폭을 변경하여 DOB의 제어 이득 조절이 가능하다.

Fig. 5

Structure of the current controller and current DOB

PID 위치 제어기과 위치 DOB를 Fig. 6에 나타냈다. 위치 DOB는 일자유도 강체와 전자석의 전류-힘 이득을 이용하여 구현하였다. 병렬형 PID 위치 제어기를 사용했고 선형 위치 DOB에서 KI는 전자석 전류-힘 이득, wcc3은 저역 통과 필터 차단 주파수, m은 쇠공 질량이다.

Fig. 6

Structure of the PID controller and position DOB

5. 외란 제거와 초기 부상 실험

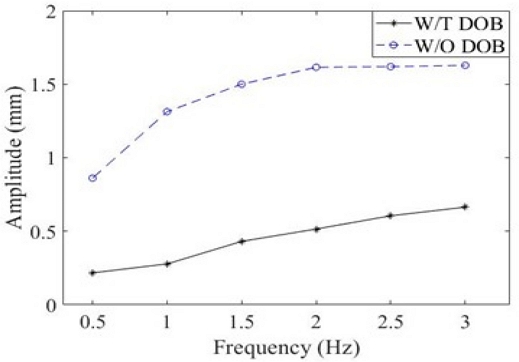
선형 위치 DOB의 정현 외란 제거 성능을 Fig 7에 나타냈다. 위치 제어에 DOB를 적용한 후에 주파수 0-3 Hz 범위 외란은 평균 69.1%정도 제거되지만 주파수가 증가할수록 외란 제거 성능이 저하된다.

Fig. 7

Disturbance rejection of the MLS with position DOB

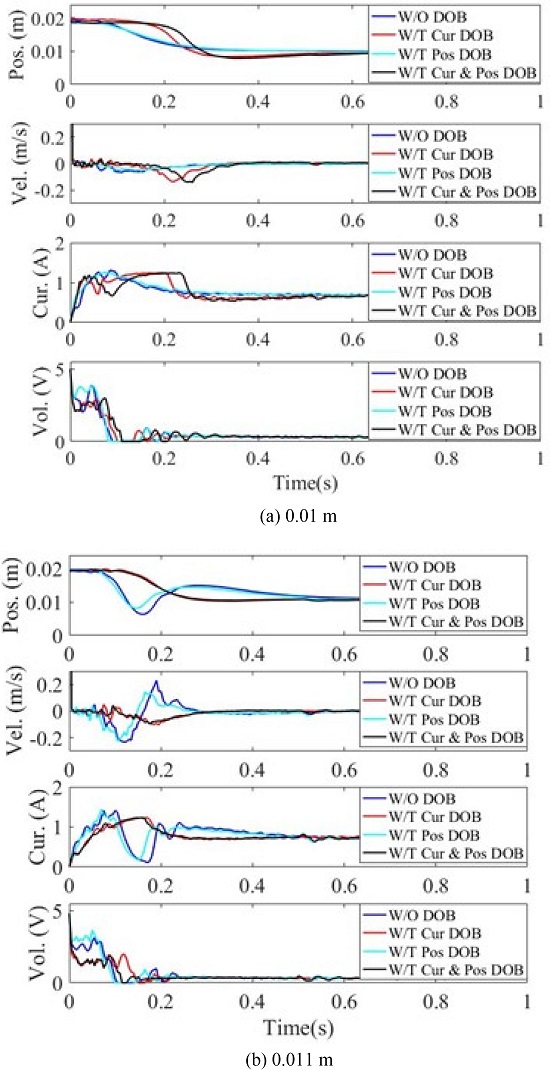
전류 및 위치 DOB 유무에 따른 초기 부상 응답을 Fig. 8에 나타냈다. Fig. 8(a)는 평형점 0.01 m 그리고 Fig. 8(b)는 0.011 m에서의 부상 결과이다. Fig. 8(a)와 같이 위치 DOB는 제어 이득을 증가하여 상승 시간을 줄이지만 Fig. 8(b)와 같이 평형점에서 10%(0.001 mm)만 벗어나도 전류 및 위치 제어 안정성이 떨어진다. 위치 DOB가 제어 이득을 높이지만 시스템 안정성이 떨어뜨린다. 위치 DOB와 함께 전류 DOB를 추가하면 평형점에 따른 모델 변동을 보상하여 Fig. 8(b)와 같이 초기 부상 시 전류와 속도 변동을 크게 줄여 안정성이 향상된다. 그 결과 평형점이 0.011 mm일 때 위치 DOB만 사용한 결과와 비교하여 정착 시간이 평균 0.15 s, 최대 오버슈트(Overshoot)가 평균 37.7% 감소되었다.

Fig. 8

Initial levitation W/T and W/O current and position DOBs

6. 제어기 최적화

6.1 주파수 응답 측정

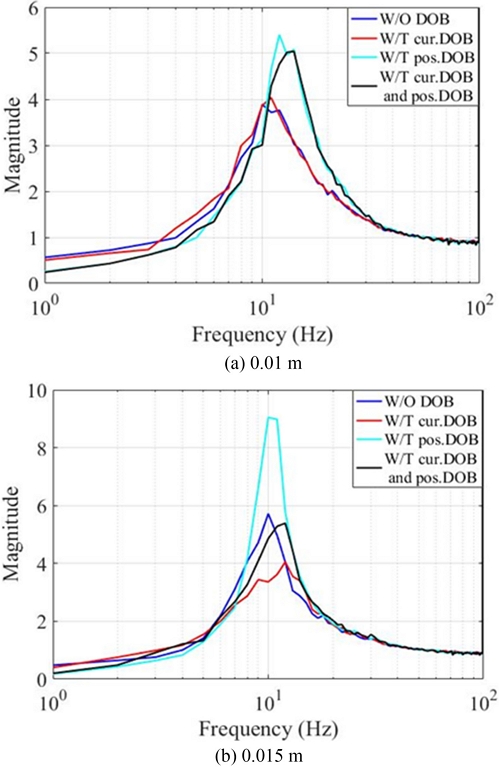
단일 정현파 가진으로 전류 및 위치 DOB 유무와 평형점에 따른 민감도 함수를 Fig. 9에 나타냈다. 전류 및 위치 DOB 차단주파수가 각각 30과 15 rad/s이며 평형점은 각각 0.01과 0.015 m이다.

Fig. 9

Sensitivity functions W/T and W/O current and position DOB

Fig. 9(a)와 같이 위치 DOB 경우 제어 이득 증가로 고유 진동수가 높아지고 제어 대역폭은 늘어나지만 민감도 함수 최댓값이 4에서 5.5로 증가하여 안정성이 나빠진다. 평형점 위치 변화가 없고 모델 불확실성이 적으면 전류 DOB는 안정성(민감도 함수 최댓값)에 큰 영향을 미치지 않는다. 반면 평형 위치를 0.015 mm로 변경된 Fig. 9(b)에서 위치 DOB는 평형점의 작은 변화에도 민감도 함수 최댓값이 크게 5.7에서 9로 크게 증가하지만 전류 DOB와 함께 사용하면 늘어난 대역폭은 유지하며 민감도함수 최댓값을 다시 5.5로 줄여 안정성을 향상시킬 수 있다. 즉, 전류 제어 DOB는 모델 불확정성으로 인한 MLS 안정성 하락을 일정 정도 보상할 수 있다.

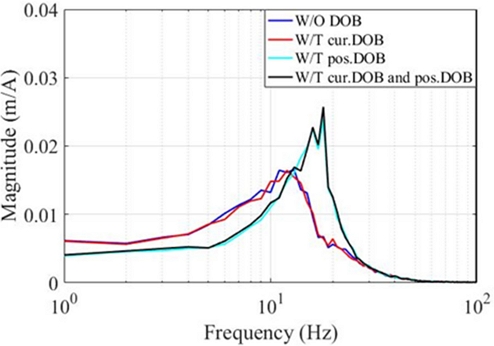
외란 제거 성능을 확인하기 위해 평형 위치 0.01 m에서 전류 및 위치 DOB 유무에 따른 부하 외란 민감도 함수(P/(1+PC))를 Fig. 10에 나타냈다. DOB를 사용하지 않은 경우 대비 위치 제어 DOB는 10 Hz까지 우수한 외란 제거 성능을 보이며 전류 DOB는 위치 외란 제거에 영향을 주지 않는다.

Fig. 10

Disturbance sensitivity functions of the MLS W/T and W/O current and position DOB

6.2 DOB 성능 최적화

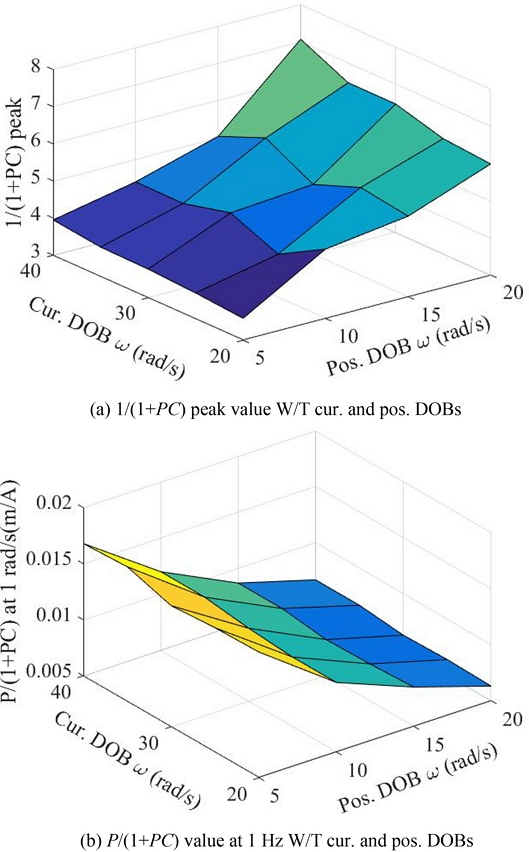
전류와 위치 DOB를 적용하고 전류 DOB 차단 주파수를 20부터 40 rad/s까지 5 rad/s씩, 위치 DOB 차단 주파수를 5부터 20 rad/s까지 5 rad/s씩 변화시키며 민감도 함수 최댓값과 1 Hz에서의 외란 민감도 함숫값을 Fig. 11에 나타냈다. Fig. 11(a)와 같이 안정성을 높이려면 위치 및 전류 DOB 차단 주파수를 낮춰야 하지만 Fig. 11(b)와 같이 위치 DOB 차단 주파수를 높여 외란 제거 성능을 향상시킬 수 있다. 또한 전류 DOB를 이용해 위치 DOB 사용으로 인한 안정성 문제를 완화할 수 있다. 외란 제거 성능을 높이며 민감도 함수 최댓값이 5 이하가 되도록 전류 DOB 차단 주파수를 30, 위치 DOB 차단 주파수를 15 rad/s로 결정하면 안정성과 외란 제거 성능을 조율할 수 있다.

Fig. 11

Sensitivity functions of the MLS W/T various cut-off frequencies of the current and position DOB

7. 결론

이 논문에서는 MLS의 DOB 기반 제어 강화에 대해 연구했다. DOB를 PI 전류 제어에 적용하여 쇠공 위치에 따른 인덕턴스 변화를 보상하였고 PID 위치 제어에 DOB를 적용하여 외란 제거 성능을 향상시켰다. DOB 기반 제어 강화 효과를 정현파 외란 제거 초기 부상 그리고 폐루프 주파수 응답 측정을 통해 확인하였다. 마지막으로 전류 및 위치 DOB 차단 주파수를 변경하며 외란 제거 성능과 시스템 안정성을 조율할 수 있음을 확인하였다.

Acknowledgments

이 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구입니다(RS-2023-00242282).

REFERENCES

• Yang, Z.-J., Miyazaki, K., Kanae, S., Wada, K., (2004), Robust position control of a magnetic levitation system via dynamic surface control technique, IEEE Transactions on Industrial Electronics, 51(1), 26-34. [https://doi.org/10.1109/TIE.2003.822095]
• Yoo, S. J., Kim, S., Cho, K.-H., Ahn, H.-J., (2021), Data-driven self-sensing technique for active magnetic bearing, International Journal of Precision Engineering and Manufacturing, 22(6), 1031-1038. [https://doi.org/10.1007/s12541-021-00525-x]
• Wan, S., Li, X., Su, W., Hong, J., (2022), Milling chatter mitigation with projection-based robust adaptive controller and active magnetic bearing, International Journal of Precision Engineering and Manufacturing, 23(12), 1453-1463. [https://doi.org/10.1007/s12541-022-00710-6]
• Balko, P., Rosinová, D., (2017), Modeling of magnetic levitation system, Proceedings of the 2017 21st International Conference on Process Control (PC), 252-257. [https://doi.org/10.1109/PC.2017.7976222]
• Radke, A., Gao, Z., (2006), A survey of state and disturbance observers for practitioners, Proceedings of the 2006 American Control Conference. [https://doi.org/10.1109/ACC.2006.1657545]
• Shim, H., Park, G., Joo, Y., Back, J., Jo, N. H., (2016), Yet another tutorial of disturbance observer: Robust stabilization and recovery of nominal performance, Control Theory and Technology, 14(3), 237-249. [https://doi.org/10.1007/s11768-016-6006-9]
• Yamato, S., Nakanishi, K., Suzuki, N., Kakinuma, Y., (2021), Development of automatic chatter suppression system in parallel milling by real-time spindle speed control with observer-based chatter monitoring, International Journal of Precision Engineering and Manufacturing, 22(2), 227-240. [https://doi.org/10.1007/s12541-021-00469-2]
• Chen, Y.-C., Cai, Y.-R., Cheng, M.-Y., Su, K.-H., (2023), Disturbance suppression and contour following accuracy improvement: An adaptive pi-type sliding mode nonlinear extended state observer approach, International Journal of Precision Engineering and Manufacturing, 24(3), 353-370. [https://doi.org/10.1007/s12541-022-00754-8]
• Kang, N.-S., Jo, N.-H., (2013), A study on the controller design for ems system using disturbance observer, The Transactions of the Korean Institute of Electrical Engineers, 62(9), 1264-1269. [https://doi.org/10.5370/KIEE.2013.62.9.1264]
• Jo, N.-H., (2022), A study on a reduced-order disturbance observer controller for nonlinear electro-magnetic suspension systems, Transactions of the Korean Institute of Electrical Engineers, 71(1), 196-202. [https://doi.org/10.5370/KIEE.2022.71.1.196]
• Zheng, Y. P., Ahn, H. -J., (2023), Control performance improvement of a nonlinear magnetic levitation system with a disturbance observer, Journal of the Korean Society for Precision Engineering, 40(4), 329-334. [https://doi.org/10.7736/JKSPE.022.133]
• INTECO, MLS (Magnetic Levitation Systems). https://www.inteco.com.pl/products/magnetic-levitation-systems/