강화학습에 기반한 전기차의 에너지 최적 주행제어

1. 서론

산업의 지속적인 발전으로 인해 온실가스 배출량 증가로 인한 지구온난화 및 환경 문제에 대한 국제적인 관심이 증가하고 있다. 특히, 차량 분야의 온실가스 배출량을 줄이고자 자동차 시장은 기존 내연기관 차량에서 Electric Vehicle(전기 자동차), Hybrid Electric Vehicle(하이브리드 자동차), Fuel Cell Electric Vehicle(수소 연료전지 자동차)과 같은 친환경 차에 대한 관심이 증가하고 있다.

이와 같은 전동화 차량의 개발과 함께, 차량 자체를 보다 효율적으로 주행함으로써, 차량의 연료 소모량을 줄이는 에코 드라이빙(Eco-driving) 분야에 관한 연구도 활발히 이루어지고 있다. Eco-driving은 차량을 통해 사람이나 화물을 이동 시에, 에너지 소비를 줄이는 주요 전략으로 인식되고 있으며, 특정 주행 환경에서 에너지 소모가 동일하지 않은 여러 가지 방법이 있다는 아이디어에 기반한다. 특히 Eco-driving 기술은 자율주행 자동차 시대에 운전자 없이 최적의 속도 프로파일, 또는 운전 방식 등을 찾음으로써 에너지 소모율을 줄일 수 있는 중요한 전략이다[1,2].

Eco-driving 제어 관련하여서는 다양한 연구가 진행되어왔으며, 크게 규칙 기반(Rule Based) 방법론과 최적화 기반(Optimization Based) 방법론으로 구분할 수 있다. 규칙 기반 방법론은 실제 경험이나 실험 결과를 토대로 에너지 소모를 줄일 수 있지만 주행 상황에서 구체적인 최적화된 솔루션이 아닐 수 있다. 반면 최적화 기반 방법론은 최적화 알고리즘을 통해 차량 제어 전략을 최적화한다. 계산 복잡성이 존재하지만, 이론적으로 에너지를 최적으로 관리할 수 있다[3]. 이러한 최적화 기반 Eco-driving 전략에는 Dynamic Programming (DP), Model Predictive Control (MPC), Reinforcement Learning (RL) 등이 있다.

Mensing 등[4–6]은 DP 알고리즘을 운전자를 위한 최적의 속도를 계산하는 데 사용하였지만, 이 알고리즘은 계산 시간이 매우 오래 걸리기 때문에 실시간 응용에 적합하지 않다. Han 등[7]은 EV 주행 시 선행 차량과의 안전거리 및 제한 속도를 상태 제약 변수로 설정하였으며 MPC 알고리즘을 사용하여 알고리즘 계산 시간 감소, 해석적 상태 제약 솔루션을 도출했다. 또한, Santin 등[8,9]은 적응형 비선형 MPC를 활용하여 표준 생산 파워트레인 제어 모듈이 장착된 차량을 구현했다. Abbsa 등[10]은 EV의 Eco-driving을 위해 Pontryagin’s Maximum Principle (PMP)과 예를 함께 사용했다. PMP 알고리즘은 필요조건을 충족하는 운전 모드를 찾기 위해 사용되었고, 그런 다음 DP가 최적 제어 문제를 거리 영역에서 다시 해결하기 위해 사용되어 DP 계산의 계산 부담을 줄였다. 하지만 MPC, PMP 등의 알고리즘은 로컬 최적해에 중점을 두고 있어 글로벌 최적해를 찾는 것이 아니라는 한계가 있다[2].

본 논문에서는 강화학습 알고리즘을 사용하여 Eco-driving 전략을 수립했다. 강화학습은 환경과 에이전트 간의 상호 작용을 통해 최적 제어 정책을 학습할 수 있는 알고리즘이다[11]. 강화 학습은 DP 알고리즘과 벨만 방정식을 기반으로 한다는 점에서 유사한 성질을 가진다. 따라서 DP 기반 방법을 RL 알고리즘을 통해 접근하는 방법으로 대체할 수 있다. 여기서 DP와 달리 강화학습은 확률적 방법으로 학습을 하며 실시간 컨트롤러로 사용될 수 있다. 따라서 복잡하고 다양한 주행 환경에서 확률적인 관점을 통해 최적의 솔루션을 찾아야 하는 Eco-driving에 적합하다[2]. Lee 등[12]은 도로의 구배와 차량 추종을 고려한 EV의 Eco-driving을 위해 Model Based Reinforcement Learning (MBRL) 알고리즘을 사용했으며, 최적의 해를 얻을 수 있는 DP와 MBRL의 결과를 비교했다. Ma 등[13]은 Multi-objective Deep Q-learning (MOM-DQL)이 Eco-routing 문제에 활용되어 최적의 경로를 찾아 주행 시간과 연료 소비를 최소화하였다. Shi 등[14]은 고립된 신호 교차로 근처에서 Q-learning 알고리즘을 사용하여 연료 소비를 최소화하는 Eco-driving을 위해 차량 주행 동작을 최적화했다. Guo 등[15]은 종방향 가/감속뿐만 아니라 횡방향 차선 변경까지 고려하는 Hybrid RL 알고리즘을 통해 주행 시간을 유지하면서 연료 소모율을 크게 줄였다.

본 논문에서는 구배가 있는 도로 환경에서 전기자동차의 에너지 효율을 개선하기 위한 Eco-driving 전략에 대해, Deep Q-network (DQN) 및 Deep Deterministic Policy Gradient (DDPG) 알고리즘을 활용하여 연구를 진행하였다. 시뮬레이션을 기반으로 연구가 진행되었으며, Eco-driving 전략의 성능검증을 위해 기존의 크루즈 모드 주행과 에너지 소모량을 비교하였다. 크루즈 모드 주행은 차량을 일정한 속도로 주행하기 때문에 다양한 도로 환경에서 차량의 에너지 소모량을 최소화하는 최적의 주행 전략으로 보기 어렵다. 따라서 강화학습을 적용하여 에너지 효율을 최적화한 EV의 전비 성능을 크루즈 모드 주행과 비교하여 연비 향상도를 검증하였다.

본 논문은 다음과 같이 구성된다. 2절에서는 본 연구에서 활용된 전기차 시뮬레이션 모델에 대해서 소개하고, 3절에서는 Eco-driving을 위한 강화학습 알고리즘에 관해 설명한다. 4절에서는 전기차 시뮬레이션 모델에 강화학습 알고리즘을 적용한 시뮬레이션 결과를 제시하고, 마지막 5절에서는 결론을 제시한다.

2. 전기차 시뮬레이션 모델 개발

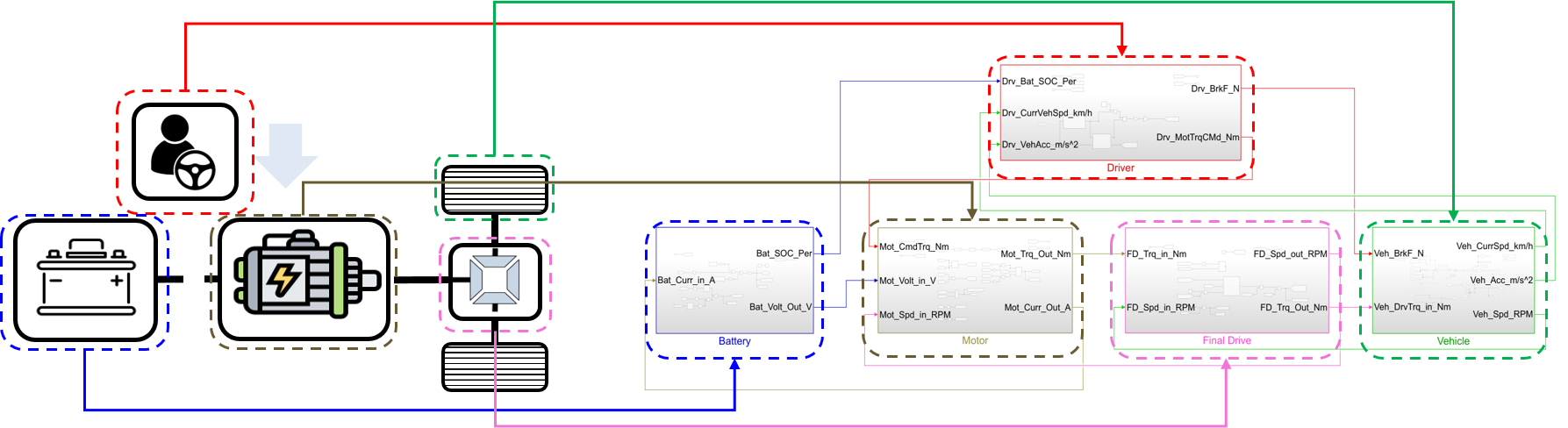
본 연구에서 사용하는 전기차 시뮬레이션 모델은 Quasi-static 모델링 방법을 사용하고, 운전자 모델, 주행 사이클, 변수들의 동역학적 상태를 고려하기 위해 Forward simulator 방식의 차량 종방향 다이나믹스를 MATLAB Simulink를 통해 구성한다.

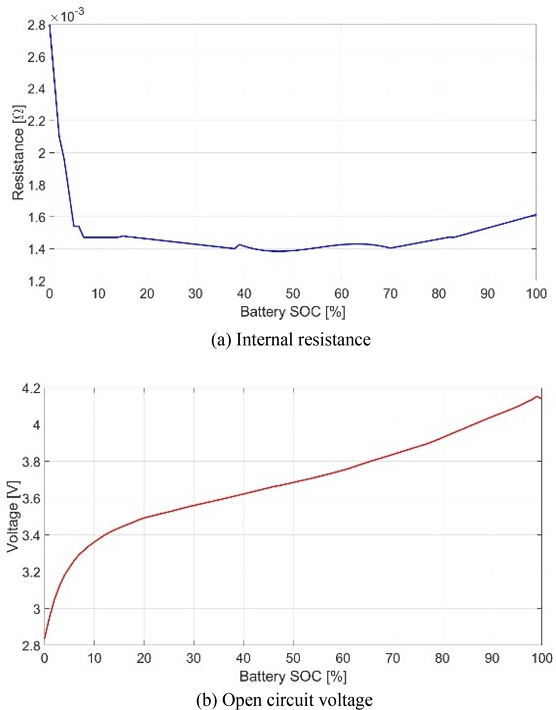
전기차 시뮬레이터는 Fig. 1과 같이 배터리, 모터, Final Drive, 차량 동역학, 운전자 모델로 구성된다. 배터리 모델은 식(1)과 같이 배터리의 내부 저항과 Open Circuit Voltage를 통해 Sate of Charge (SOC)에 대한 식으로 나타낸다.

Fig. 1

EV simulator with battery, motor, final drive, vehicle and driver model for eco-driving

배터리의 SOC에 따른 내부 저항과 Open Circuit Voltage는 Fig. 2와 같다.

Fig. 2

Internal resistance and open circuit voltage with SOC

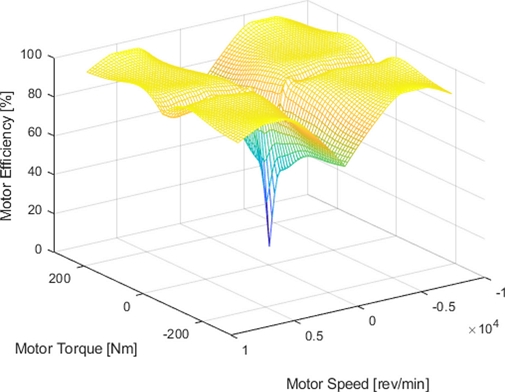
모터 모델은 모터 RPM, 모터 토크를 통한 모터 효율 맵을 통해 정해진 효율을 통해 모터 출력 동력이 결정된다. 모터 출력 동력에 대한 수식은 식(2)와 같으며 모터 효율 맵은 Fig. 3과 같다.

Fig. 3

Motor efficiency map by motor rpm and motor torque

Final Drive 모델은 별도의 효율 맵을 구성하지 않고 96%의 효율과 기어비는 7.4로 구성한다.

차량 동역학 모델은 식(3)과 같이 1차원 종방향 다이나믹스로 구성되며 식(4)에서 Table 1의 도로 부하 계수를 사용한다.

Table 1

Vehicle specification

운전자 모델은 Reference 속도와 현재 속도 차이에 대한 PID 제어를 통해 모터의 요구 토크를 생성한다. 또한, 회생 제동은 PID 제어 신호에서 음수인 브레이크 신호가 발생하고 10 km/h 이상의 차속인 상황에서 100% 작동하도록 가정한다.

시뮬레이터에 사용된 차량 제원은 Table 1과 같다.

3. 강화학습 알고리즘

3.2 DQN 알고리즘

Deep Q-Network (DQN) 알고리즘은 Q-learning을 기반으로 학습하고, Q function을 업데이트하는 알고리즘이다. DQN 알고리즘은 연속적인 Observation 공간과 이산화된 Action 공간을 사용한다. Q function이 업데이트되는 원리는 식(7)과 같다.

$\[ Q\left(s_t,a_t\right)\leftarrow Q\left(s_t,a_t\right)+\alpha \left[R_{t+1}+\gamma \underset{a}{max}Q\left(s_{t+1},a\right)-Q\left(s_t,a_t\right)\right] \]$

(7)

처음 제안된 DQN 알고리즘은 샘플들 사이의 Temporal Correlation과 Target이 고정되지 않는 문제점이 있었고, 이를 해결하기 위해 Experience Replay와 Target 네트워크를 사용했다. Experience Replay를 사용함으로써 Temporal Correlation이 줄어들고 추가로 미니 배치를 활용함으로써 학습 속도가 빨라졌다. 또한, 같은 샘플을 재사용함으로써 데이터 효율이 증가했다. Mnih 등[16,17]의 연구에서, Target 네트워크는 Behavior 네트워크가 업데이트되는 동안 실시간으로 업데이트되지 않고 일정 스텝 후에 Behavior 네트워크로 업데이트됨으로써 네트워크 업데이트에 따라 수렴에 어려움이 발생했던 문제를 개선했다. 이 2가지 개선점이 적용된 Loss Function은 Gradient Descent 방식을 사용하여 Loss Function이 최소화되도록 네트워크를 업데이트한다. Loss Function은 식(8)과 같다.

$\[ L\left(\theta \right)=\frac{1}{B}\sum _{\left|\left\{i\right\}\right|=B}{\left[r_{i+1}+\gamma \underset{a}{max}\widehat{Q}\left(s_{i+1},a;\widehat{\theta }\right)-Q\left(s_i,a_i;\theta \right)\right]}^2 \]$

(8)

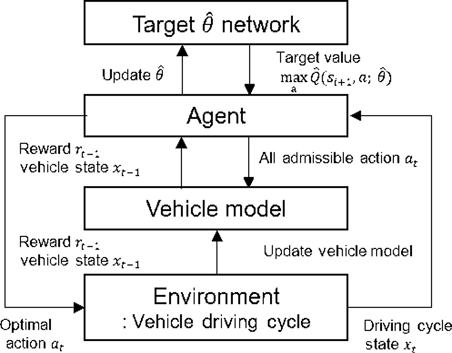
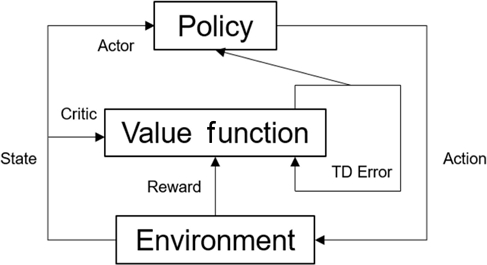
DQN 알고리즘이 적용되는 원리는 Fig. 4와 같다.

Fig. 4

DQN algorithm

본 논문에서 DQN 알고리즘을 적용하기 위해 다음과 같이 알고리즘 모델을 설정했다. 첫째, Observation은 v, Alt, slope, SOC, v_error, ∫v_error이다. 둘째, Action인 가속도를 -3부터 3까지의 범위로 이산화하여 연구를 진행했다. 마지막으로, 목적함수는 식(5)와 같으며 Cost는 식(6)과 같다. 또한, DQN 알고리즘에서의 파라미터에 따른 경향성을 확인하기 위해 1) 학습률 10^-2-10^-6에 따라, 2) Action의 이산화 수 1, 10, 50, 100, 1000에 따라, 3) 가중치 계수 γ를 1, 10, 50, 100, 1000으로 증가시킬 때의 경향성을 확인했다.

3.3 DDPG 알고리즘

Deep Deterministic Policy Gradient (DDPG) 알고리즘은 DQN과 Deterministic Policy Gradient (DPG) 알고리즘에 기반한다. DDPG 알고리즘은 Observation 공간과 Action 공간이 연속적인 특징이 있다. 이 알고리즘은 DQN 알고리즘에서 사용되는 Loss Function의 Critic 네트워크와 DPG 알고리즘에서 사용되는 Objective Function의 Actor 네트워크를 통해 업데이트된다. Critic 네트워크는 식(9)와 같이 업데이트된다.

$\[ \varphi \leftarrow \varphi -\left\{r+\gamma {\widehat{Q}}_{\widehat{\varphi }}\left(s^{\text{'}},{\widehat{\mu }}_{\widehat{\mathrm{\theta }}}\left(s^{\text{'}}\right)\right)-Q_{\varphi }\left(s,a\right)\right\}{\nabla }_{\varphi }{Q}_{\varphi }\left(s,a\right) \]$

(9)

DPG 알고리즘에서 Gradient Ascent은 식(10)과 같고 Actor 네트워크는 식(11)과 같이 Gradient Ascent 방식으로 업데이트한다.

$\[ J\left(\theta \right)=E_{s\sim {\rho }_u}\left[Q_{\varphi }\left(s,a\right)\right] \]$

(10)

$\[ \theta \leftarrow \theta +{\left.{\nabla }_a{Q}_{\varphi }\left(s,a\right)\right|}_{a={\mu }_{\theta }\left(s\right)}{\nabla }_{\theta }{\mu }_{\theta }\left(s\right) \]$

(11)

이때 Critic 네트워크 업데이트는 DQN 알고리즘과 유사하지만, Action이 정해져 있다는 차이점이 있다. 또한, DPG 알고리즘에 의해 Policy가 결정되어 있어 알고리즘의 Variance가 낮아짐에 따라 탐험의 효과가 감소한다. 따라서 식(12)의 Extra Noise를 추가하여 탐험의 효과를 증가시킨다.

$\[ N:a_t={\mu }_{\theta }\left(s_t\right)+N_t \]$

(12)

DDPG 알고리즘은 DQN 알고리즘과 다르게 식(13)에서와 같이 τ를 조정하여 네트워크를 매번 업데이트할 수 있다.

$\[ \widehat{\varphi }\leftarrow \tau \varphi +\left(1-\tau \right)\widehat{\varphi } \]$

(13a)

$\[ \widehat{\theta }\leftarrow \tau \theta +\left(1-\tau \right)\widehat{\theta } \]$

(13b)

DDPG 알고리즘이 적용되는 원리는 Fig. 5과 같다.

Fig. 5

DDPG algorithm

본 논문에서 DDPG 알고리즘을 적용하기 위해 다음과 같이 알고리즘 모델을 설정했다. 첫째, Observation은 v, Alt, slope, SOC, v_error, ∫v_error이다. 둘째, Action인 가속도를 -3부터 3까지의 범위로 설정한다. 마지막으로, 목적함수는 식(5)와 같으며 Cost는 식(6)과 같다. 또한, DDPG 알고리즘에서의 파라미터에 따른 경향성을 확인하기 위해 1) Critic의 학습률 10^-3~10^-6에 따라, 2) Actor의 학습률 10^-3~10^-6에 따라, 3) Critic과 Actor의 학습률을 고정하고 가중치 계수 α를 0.01~0.1까지 0.01씩 증가시킬 때의 경향성을 확인했다.

4. 시뮬레이션 결과

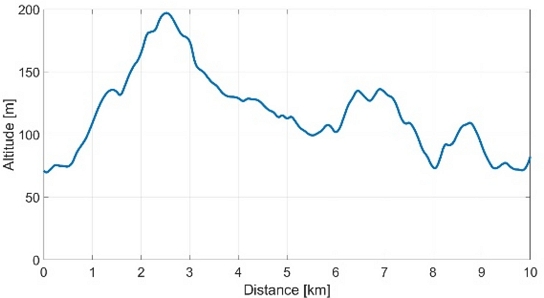
본 연구에서는 2절에서 설명한 차량 Simulink 모델을 기반으로 MATLAB 강화학습 알고리즘을 적용했으며, 주행 사이클은 총 10 km이며 거리에 따른 고도의 정보는 Fig. 6과 같다.

Fig. 6

Distance-based altitude driving cycle

또한, 초기 SOC는 100%, 초기 차량 속도는 60 km/h로 설정했다. 식(6)에서의 가중치는 식(14)와 같이 적용했으며, DQN 알고리즘의 경우 가중치 γ에 의한 경향성을 확인하고자 다른 케이스와 다른 비율을 적용했다.

학습 수렴성, 크루즈 모드 대비 SOC 개선 정도, 타깃 속도 근접성을 기준으로 강화학습의 결과 비교, 분석을 진행했다. 이때 크루즈 모드 속도는 강화학습이 적용된 시뮬레이션과 동일한 거리를 동일한 시간으로 일정하게 주행하는 속도로 선정했다.

4.1 DQN 알고리즘 결과와 크루즈 모드 결과 비교

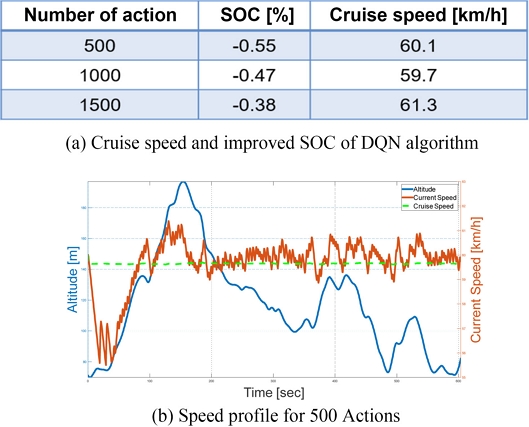
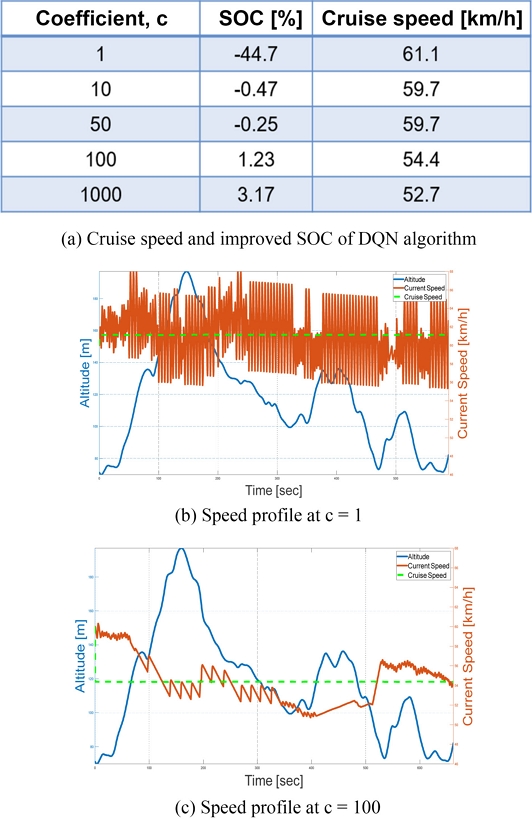
DQN 알고리즘을 적용한 연구에서는 액션 수, 학습률, 가중치 계수 γ에 따른 강화학습 결과와 파라미터에 의한 경향성을 확인했다. 먼저, Action 수에 따른 결과 비교 과정에서 사용된 파라미터는 Table 2와 같다.

Table 2

DQN algorithm parameter with respect to number of action

액션 수에 따른 DQN 알고리즘의 결과는 Fig. 7(a)와 같다. 이 케이스에서는 액션 수를 증가시킴에 따라 가속도를 더 세분화하여 나누었기 때문에 속도 프로파일의 진동이 개선되는 경향을 보였다. 또한, 고도가 증가/감소함에 따라 차량의 속도가 감소/증가하는 경향성을 확인할 수 있었으며, 액션 수가 커짐에 따라 크루즈 모드 대비 에너지 효율이 향상하는 경향을 보였다. 하지만 연속적인 값을 가지는 차량의 속도, 가속도와 같은 변수를 이산화하여 계산하고, 이를 충분하지 않은 에피소드에서 학습을 진행시켰기에 학습의 성능이 좋지 않다고 생각된다. 이러한 문제는 액션 수와 에피소드 수를 증가시키면 더 많은 학습이 되므로 개선될 것으로 예상된다.

Fig. 7

DQN algorithm parameter with respect to number of action

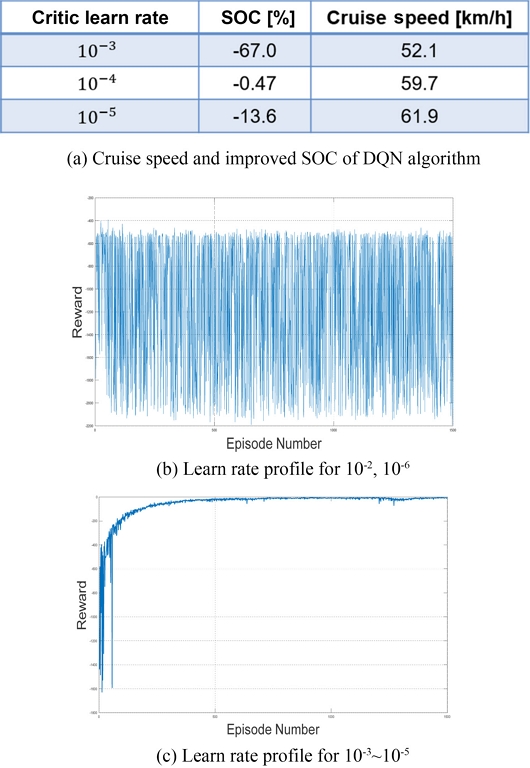
다음으로, 학습률에 따른 결과 비교 과정에서 사용된 파라미터는 Table 3과 같다.

Table 3

DQN algorithm parameter with respect to learn rate

학습률에 따른 결과는 Fig. 8(a)와 같다. Fig. 8(b)에서와 같이 학습률이 10^-2, 10^-6에서는 학습이 수렴하지 않았으며, 이 케이스를 통해 학습률이 10^-4에서 가장 안정적으로 학습이 되었고 학습 속도가 너무 빠르거나 너무 느리면 학습이 안정적으로 수렴하지 않는 경향성을 확인할 수 있다.

Fig. 8

DQN algorithm parameter with respect to learn rate

앞서 진행한 연구에서 학습된 속도 프로파일들이 진동하는 경향을 보였으며 이를 개선하고자 가중치 계수 γ에 따른 결과를 비교하는 연구를 진행했다. 가중치 계수 γ에 따른 결과 비교 과정에서 사용된 파라미터는 Table 4와 같다.

$\[ \beta =c\alpha \]$

(15)

Table 4

DQN algorithm parameter with respect to weighting coefficient γ

이때 가중치 계수 γ를 앞선 연구에서 사용된 계수 10α 뿐만 아니라 식(15)와 Table 4와 같이 다양한 케이스에 대해 연구를 진행했다.

가중치 계수 γ에 따른 결과는 Fig. 9(a)와 같다. Figs. 9(b), 9(c)와 같이 가중치 계수 γ를 증가시킴에 따라 속도 프로파일의 진동이 감소하는 경향을 확인할 수 있었고, 이 결과를 통해 차량 운전성이 향상되었다고 볼 수 있다.

Fig. 9

DQN algorithm parameter with respect to weighting coefficient γ

DQN 알고리즘을 적용한 EV 시뮬레이터의 결과는 학습 수렴성, 크루즈 모드 대비 SOC 개선정도 등을 고려했을 때, 전반적으로 학습이 안정적으로 되지 않았다. 이에 대한 이유는 액션 공간을 이산화하는 DQN 알고리즘의 특성에 의한 것이라 생각된다. 연속적인 차량 시스템 모델을 이산화된 시스템으로 변환하는 과정에서 차량 시스템의 특성을 충분히 반영하지 못하고 이에 따라 학습의 성능이 저하될 수 있다. 본 연구에서 사용된 에피소드보다 더 많은 에피소드 수로 학습을 시키고, 액션을 이산화하는 과정을 연속 시스템에 유사하도록 더 세분화하는 방법을 통해 DQN 알고리즘의 학습 성능을 향상시킬 수 있을 것으로 생각된다.

4.2 DDPG 알고리즘 결과와 크루즈 모드 결과 비교

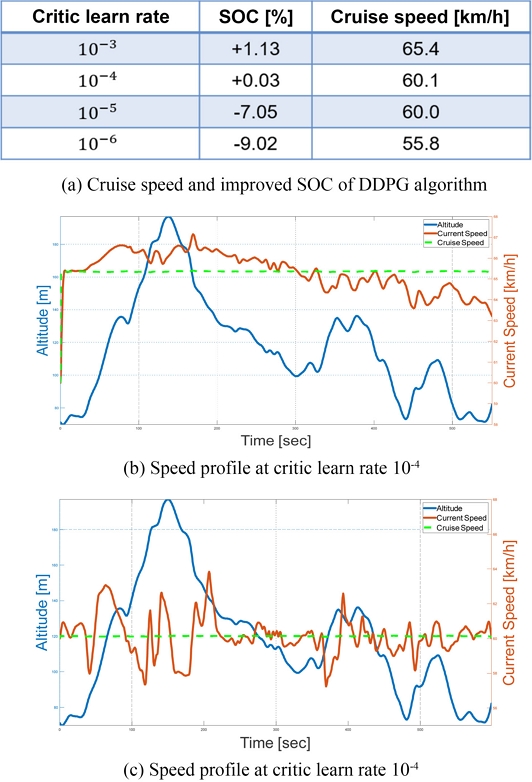
DDPG 알고리즘을 적용한 연구에서는 Critic 학습률, Actor 학습률, 가중치 계수 α에 따른 강화학습 결과와 파라미터에 의한 경향성을 확인했다. 먼저, Critic 학습률에 따른 결과 비교 과정에서 사용된 파라미터는 Table 5와 같다.

Table 5

DDPG algorithm parameter with respect to critic learn rate

이때 Critic 학습률에 따른 결과는 Fig. 10(a)와 같다. 학습률이 10^-2일 때는 Fig. 8(b)와 같은 학습 수렴성을 보이며, 학습률이 10^-5인 케이스에서는 에너지 소모율이 악화되었다는 점에서 Critic 학습률이 너무 느리거나 빠르면 학습이 안정적으로 되지 않는 것을 확인할 수 있었다.

Fig. 10

DDPG algorithm parameter with respect to critic learn rate

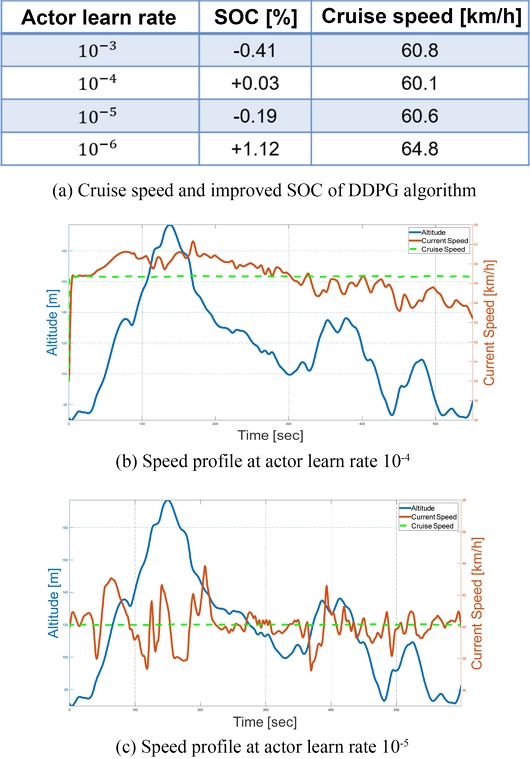
다음으로, Actor 학습률에 따른 결과 비교 과정에서 사용된 파라미터는 Table 6과 같다.

Table 6

DDPG algorithm parameter with respect to actor learn rate

Actor 학습률에 따른 결과는 Fig. 11(a)와 같으며, 학습률이 10^-2인 케이스를 제외한 모든 케이스에서 학습은 수렴하였다. 학습률이 너무 빠른 케이스에서는 동일한 경향을 보이지만, Critic 학습률에 따른 결과에 비해 Actor 학습률의 변화에 대해서 전체적으로 학습이 안정적으로 되었음을 확인할 수 있었다. 이를 통해 이 시스템에는 Actor 학습률보다 Critic 학습률의 영향이 큰 것을 확인할 수 있었다.

Fig. 11

DDPG algorithm parameter with respect to actor learn rate

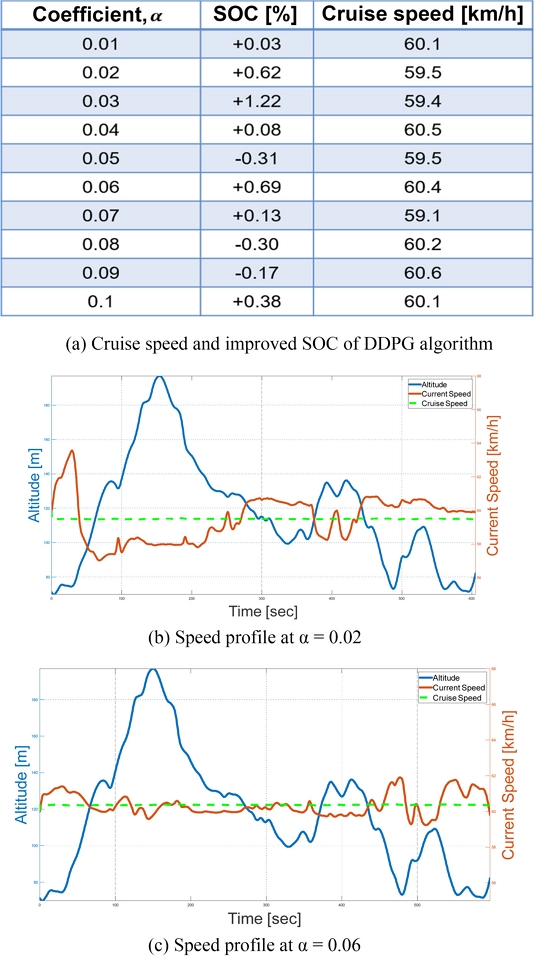
마지막으로 전체 Cost에 따른 결과를 확인하고자 가중치 계수 α의 변화에 따른 결과를 비교하는 연구를 진행했다. 가중치 계수 α에 따른 결과 비교 과정에서 사용된 파라미터는 Table 7과 같다.

Table 7

DDPG algorithm parameter with respect to weighting coefficient α

가중치 계수 α에 따른 결과는 Fig. 12(a)와 같으며, 이 결과를 통해 다양한 케이스에서 에너지 효율이 개선되었음을 확인했다. 경사가 있는 도로를 주행할 때, EV 파워트레인의 개입 없이 운동에너지가 위치에너지로, 위치에너지가 운동에너지로 직접 변환되는 과정을 통해 전기차 에너지 효율이 증가될 수 있다. Figs. 12(b), 12(c)에서 고도가 높아질 때 속도는 감소하고, 고도가 낮아질 때 속도는 증가하는 경향을 확인할 수 있으며 두 케이스에서 모두 에너지 효율이 개선되었음을 Fig. 12(a)에서 확인할 수 있다.

Fig. 12

DDPG algorithm parameter with respect to weighting coefficient α

DDPG 알고리즘을 적용한 EV 시뮬레이터의 결과는 DQN 알고리즘과 비교했을 때, 전반적으로 안정적인 학습 결과를 보였다. 또한, DDPG 알고리즘의 연속적인 액션 공간 특성으로 인해 학습 과정에서 차량 시스템의 특성이 잘 반영되었다고 할 수 있다. 본 연구에서 DDPG 알고리즘을 활용하여 에너지 효율 증가 원리를 만족하는 EV의 속도 프로파일을 도출할 수 있었다.

5. 결론

본 논문은 Eco-driving 제어 방법 중 RL을 활용하여 EV의 에너지 효율을 개선하고자 했으며 강화학습 알고리즘이 효과적으로 적용될 수 있음을 확인했다. 또한, DQN 알고리즘과 DDPG 알고리즘에 따른 결과와 각 알고리즘의 파라미터에 따른 경향성을 확인할 수 있었다. DQN 알고리즘에 의한 결과는 크루즈 주행 모드 대비 에너지 소모율이 악화되었는데, 이에 대한 이유는 액션 공간을 이산화하는 DQN 알고리즘의 특성에 의한 것이라 생각된다. 시스템을 이산화하는 과정에서 연속적인 차량 시스템을 충분히 반영하지 못함에 따라 학습 성능이 저하될 수 있으며, 이러한 문제점은 더 많은 에피소드 수와 액션을 더 세분화하는 방법을 통해 개선될 수 있을 것으로 생각된다. DDPG 알고리즘을 적용한 결과에서는 전반적으로 안정적인 학습을 보였다. 또한, 연속적인 차량 시스템이 학습 과정에 잘 반영되어 에너지 효율이 개선되는 결과를 도출할 수 있었다. 본 연구의 결과를 통해 운전자의 개입 없이 최적의 속도 프로파일, 또는 운전 방식 등을 찾음으로써 해당 알고리즘을 실제 차량에 적용한다면, Cruise 모드 대비 에너지 소모율을 줄일 수 있을 것으로 생각된다.

본 연구에서는 도로의 구배 정보만으로 Eco-driving 제어 기반 속도 프로파일을 도출하였지만, 추후 연구에서는 선행 차량과의 안전거리, 신호 체계 등을 고려하여 EV 시뮬레이터 모델을 보완하고, DQN, DDPG 알고리즘 이외의 DP, MBRL 등과 같은 알고리즘을 적용하여 성능 비교 연구를 진행하고자 한다.

Acknowledgments

이 논문은 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임 (P0017120, 2024년 산업혁신인재성장지원사업).

REFERENCES

• Dib, W., Chasse, A., Moulin, P., Sciarretta, A., Corde, G., (2014), Optimal energy management for an electric vehicle in eco-driving applications, Control Engineering Practice, 29, 299-307. [https://doi.org/10.1016/j.conengprac.2014.01.005]
• Lee, H. Y., Kim, N. W., Cha, S. W., (2020), Model-based reinforcement learning for eco-driving control of electric vehicles, Journal of the Institute of Electrical and Electronics Engineers Access, 8, 202886-202896. [https://doi.org/10.1109/ACCESS.2020.3036719]
• Xu, N., Li, X., Liu, Q., Zhao, D., (2021), An overview of eco-driving theory, capability evaluation, and training applications, Sensors, 21(19), 6547. [https://doi.org/10.3390/s21196547]
• Mensing, F., Bideaux, E., Trigui, R., Tattegrain, H., (2013), Trajectory optimization for eco-driving taking into account traffic constraints, Transportation Research Part D, 18(1), 55-61. [https://doi.org/10.1016/j.trd.2012.10.003]
• Mahler, G., Vahidi, A., (2014), An optimal velocity-planning scheme for vehicle energy efficiency through probabilistic prediction of traffic-signal timing, Journal of the Institute of Electrical and Electronics Engineers Transactions on Intelligent Transportation System, 15(6), 2516-2523 [https://doi.org/10.1109/TITS.2014.2319306]
• Ozatay, E., Onori, S., Wollaeger, J., Ozguner, U., Rizzoni, G., Filev, D., Michelini, J., Cairano, S. D., (2014), Cloud-based velocity profile optimization for everyday driving: A dynamic-programming-based solution, Journal of the Institute of Electrical and Electronics Engineers Transactions on Intelligent Transportation Systems, 15(6), 2491-2505. [https://doi.org/10.1109/TITS.2014.2319812]
• Han, J. H., Sciarretta, A., Ojeda, L. L., Nunzio, G. D., Thibault, L., (2018), Safe-and eco-driving control for connected and automated electric vehicles using analytical state-constrained optimal Solution, Journal of the Institute of Electrical and Electronics Engineers Transactions on Intelligent Vehicles, 3(2), 163–172. [https://doi.org/10.1109/TIV.2018.2804162]
• Santin, O., Beran, J., Pekar, J., Michelini, J., Jing, J., Szwabowski, S., Filev, D., (2017), Adaptive nonlinear model predictive cruise controller: Trailer tow use case, (Report No. 2017-01-0090), SAE Technical Paper, (https://www.sae.org/publications/technical-papers/content/2017-01-0090/, ) [https://doi.org/10.4271/2017-01-0090]
• Santin, O., Pekar, J., Beran, J., D’amato, A., Ozatay, E., Michelini, J., Szwabowski, S., Filev, D., (2016), Cruise controller with fuel optimization based on adaptive nonlinear predictive control, SAE International Journal of Passenger Cars-Electronic and Electrical Systems, 9(2), 262-274. [https://doi.org/10.4271/2016-01-0155]
• Abbas, H., Kim, Y., Siegel, J. B., Rizzo, D. M., (2019), Synthesis of pontryagin's maximum principle analysis for speed profile optimization of all-electric vehicles, Journal of Dynamic Systems, Measurement, and Control, 141(7), 071004. [https://doi.org/10.1115/1.4043117]
• Lewis, F. L., Vrabie, D., (2009), Reinforcement learning and adaptive dynamic programming for feedback control, Journal of the Institute of Electrical and Electronics Engineers Circuits and Systems Magazine, 9(3), 32–50. [https://doi.org/10.1109/MCAS.2009.933854]
• Lee, H., Kim, K., Kim, N., Cha, S. W., (2022), Energy efficient speed planning of electric vehicles for car-following scenario using model-based reinforcement learning, Applied Energy, 313, 118460. [https://doi.org/10.1016/j.apenergy.2021.118460]
• Ma, X., Xie, Y., Chigan, C., (2019), Meta-deep q-learning for eco-routing, Proceedings of the 2019 Institute of Electrical and Electronics Engineers 2nd Connected and Automated Vehicles Symposium(CAVS), 1–5. [https://doi.org/10.1109/CAVS.2019.8887764]
• Shi, J., Qiao, F., Li, Q., Yu, L., Hu, Y., (2018), Application and evaluation of the reinforcement learning approach to eco-driving at intersections under infrastructure-to-vehicle communications, Transportation Research Record: Journal of the Transportation Research Board, 2672(25), 89–98. [https://doi.org/10.1177/0361198118796939]
• Guo, Q., Angah, O., Liu, Z., Ban, X. (J.), (2021), Hybrid deep reinforcement learning based eco-driving for low-level connected and automated vehicles along signalized corridors, Journal of the Transportation Research Part C: Emerging Technologies, 124, 102980. [https://doi.org/10.1016/j.trc.2021.102980]
• Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, L., Wierstra, D., Riedmiller, M., (2013), Playing Atari with Deep Reinforcement Learning, arXiv preprint arXiv:1312.5602, .
• Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Bellemar, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., Ostrovski, G., Peterson, S., Beattie, C., Sadik, A., Antonoglou, L., King, H., Kumaran, D., Wierstra, D., Legg, S., Hassabis, D., (2015), Human-level control through deep reinforcement learning, Nature, 518, 529–533. [https://doi.org/10.1038/nature14236]