반응표면법을 이용한 유도가열식 전기레인지 코일 형상 최적 설계 기법

1. 서론

코일에 고주파 전류를 인가했을 때 자기장의 크기가 변화하면서 유도 전류가 생성되며 이를 와전류라고 한다. 이때 철판에 와전류가 흐르게 될 경우 저항으로 인해 발열이 생기게 된다. 또한, 자기장으로 인해 철판 내부 자석들의 방향이 바뀌면서 발생하는 마찰로 손실이 발생하게 되는데 이를 히스테리시스 손이라 한다. 유도 가열이란 히스테리시스 손과 와전류 손으로 인해 발생한 손실을 이용해 물체를 가열하는 기술이며 유도 가열을 전기레인지에 적용한 것을 유도 가열식(Induction Heating, IH) 전기레인지라고 한다. 현재 상용되고 있는 IH 전기레인지는 자기장을 생성하는 가열코일과 인가전압을 조절하는 내부 회로로 구성되어 있다. 핫플레이트식 및 하이라이트식과 같은 전기레인지는 55-65%의 열효율을 갖는 데 비해 IH 전기레인지는 약 90%의 열효율이 나오며 화구에 출력을 집중할 수 있어 다른 방식의 전기레인지보다 가열 속도가 빠르다[1]. 게다가 IH 전기레인지용 조리기구는 전도체이면서 오래 사용 가능해야 하므로 보통 스테인리스 400 계열의 소재가 사용된다. 그러나 스테인리스 400 계열로 이루어진 용기는 타 소재로 이루어진 용기에 비해 열에 취약한 치명적인 단점이 있다. 그럼에도 불구하고 높은 열효율이라는 큰 장점으로 인해 IH 전기레인지는 점진적으로 더 많이 사용되고, 더 높은 출력과 열효율을 내기 위해 다양한 연구가 진행되고 있다.

Kim 등은 알루미늄, 구리 소재를 이용한 다양한 두께의 용기를 가열이 가능한 IH 전기레인지 설계를 제시하였다. 그 결과 가장 높은 효율을 보이는 용기를 선정하였으나 IH 전기레인지의 다양한 변수 중 온도 변화만을 선정하여 기존 모델과 개선점을 비교했으므로 다양한 변수를 고려한 최적 설계가 필요하다[2]. Lim은 IH 전기레인지의 다양한 변수가 성능에 미치는 영향을 분석하였다. 그 결과 각 변수가 인덕션 전기레인지에 미치는 영향은 파악할 수 있었지만, 데이터를 이용한 구조적 개선을 진행하지는 않아 개선 설계가 필요하다[3].

따라서, 본 연구에서는 코일의 형태에서 변경이 가능한 요소를 변수로 선정 후 반응표면법을 통해 IH 전기레인지의 최적 설계기법을 제시하였다. 특히 내부 회로가 코일에 가하는 전압 및 주파수 그리고 주요 가열 부품인 가열코일의 형태와 권선수를 변수로 설정하였다. 이를 바탕으로 각 변수 사이의 교호작용을 고려하여 동일한 전류를 인가했을 때 높은 온도를 낼 수 있는 성능을 가진 IH 전기레인지를 설계했다. 이를 통해 기존 IH 전기레인지보다 동일한 화구 크기에서 더 높은 열을 낼 수 있는 IH 전기레인지를 설계하였다. IH 전기레인지 용기의 소재로 사용되는 STS 430은 300^oC를 초과하는 온도에서 변형이 발생한다[4]. 따라서, 용기 온도가 300^oC를 넘지 않기 위한 코일의 권선 수와 구리선의 두께, 인가되는 전압 및 주파수에 대하여 최적 설계를 진행하였다. 또한, 민감도 분석을 통해 최적 설계변수들이 가열된 용기의 온도에 영향을 주는 정도를 파악했으며, 스크리닝을 통해 주요 설계변수 수를 줄인 후 실험계획을 수립하였다. 이후 반응 표면법을 통해 설정한 설계 목표에 가장 근사한 값을 내는 설계 변수 값을 도출하였고, 이를 바탕으로 유한요소 해석 프로그램인 ANSYS를 이용해 전자기장-열 연성 해석을 수행하였다[5,6]. 유한요소해석 결과를 통해 내열 온도에 가장 가까운 온도가 발생하는 코일의 형태와 전압 및 주파수 인가 조건을 설계하였다.

2. 본론

2.2 유한요소해석

2.2.1 재료의 기계적 성질

IH 전기레인지의 코일 및 용기에 사용된 소재 물성은 Table 1에 나타냈다[8]. Copper 소재 코일을 사용했으며, 코일을 받치고 있는 코어는 Ferrite를 적용하였고, 용기는 Stainless Steel이 사용된다. 용기에 사용된 Stainless Steel은 자성이 필요하기 때문에 400 계열인 STS 430을 사용한다. 이때 전용 소재로 이루어진 용기를 사용하지 않을 경우 열 효율이 떨어져 성능 감소로 이어질 수 있다.

Table 1

Material properties of FE simulation

2.2.2 해석 모델링

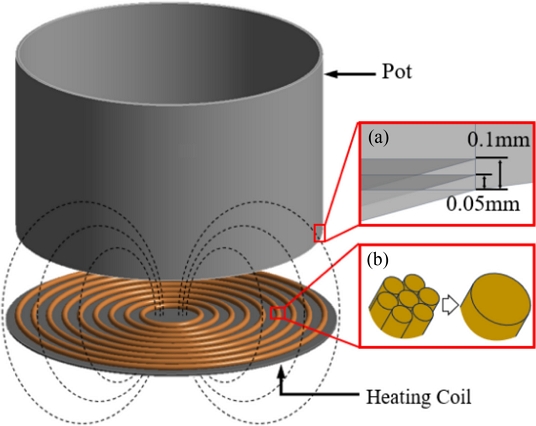
IH 전기레인지의 가열 프로세스를 구현하기 위해 연성 해석을 수행했으며 이때 사용된 모델은 3차원 CAD 프로그램 CATIA V5를 사용하여 모델링하였다. 본 연구에서는 코일로 인한 용기의 가열 프로세스에 집중하여 진행하였으므로 내부 회로는 생략하여 진행하였다. 코일은 고주파 전류에 의해 발생하는 표피효과(Skin Effect)로 인한 저항 손실을 최소화하기 위하여 단일 선이 아닌 연선 형태로 제작된다[9]. 표피효과란 교류전류를 이용할 때 주파수가 증가하면 전류의 밀도가 도체의 겉 둘레에 몰리게 되고 이때 도체의 유효면적이 감소하여 전송 손실이 증가하는 현상을 의미한다[10].

본 연구에 사용된 모델은 해석상 영향이 미미할 것으로 판단되어 Fig. 1의 (B)와 같이 여러 선으로 겹친 복잡한 형태를 단일선으로 단순화했으며 Fig. 2의 하단부에 Ring 형태를 여러 개 나열한 형태로 모델링하였다. 코일을 고정하는 역할인 코어 또한 단순한 원판 형태로 모델링하였으며, 용기의 경우 Fig. 1의 상단부와 같이 상용 스테인리스 용기와 유사한 형태로 3 mm 두께를 가진 중앙이 파인 원통형으로 모델링하였다. 각 모델링간 간격은 접촉에 가까운 형태인 0.1 mm 간격을 두고 배치하였다. 용기 모델링 시 표피(Skin Effect)를 고려하기위해 Fig. 1 (a)와 같이 용기의 하부 단면으로부터 Z축을 기준으로 0.05 mm씩 간격을 두고 면을 생성하였다.

Fig. 1

Assembly of IH Electric Stove (a)Skin effect modeling (b)Copper wire modeling

Fig. 2

Sensitivity analysis – Pareto chart

2.3 민감도 분석 및 설계 정식화

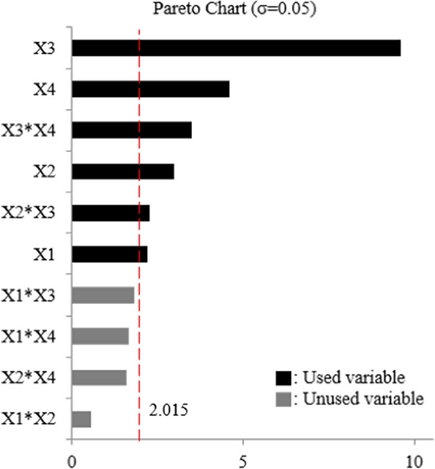
민감도 분석(Sensitivity Analysis)이란 설정한 설계변수들의 변화가 목적함수에 끼치는 영향을 파악할 때 사용된다. 설계변수의 영향도는 수치상으로 표현할 수 있으며 파레토 차트(Pareto Chart)로 나타낼 수 있다. 이는 각 변수의 수치가 클수록 목적함수에 끼치는 영향이 크다는 것을 의미한다[11]. 용기의 소재가 견딜 수 있는 내열 온도인 300^oC를 목표로 설계변수를 판별하였다. 설계변수는 코일의 구조적으로 변경이 가능한 권선 수와 두께, 변경이 가능한 전압과 주파수를 설계변수 X1, X2, X3 그리고 X4로 지정하였다. 또한 Table 2에 설계변수 범위를 나타내었다.

Table 2

Objective function and design variables

각 설계변수가 용기의 온도를 변화시키는 정도를 파악하기 위해 4요소 2수준으로 총 16번의 민감도 해석을 수행하였다. 해석 결과를 정규화(Normalization)하여 Table 3에 나타내었으며 이를 통해 얻은 파레토 차트를 Fig. 2에 나타내었다. 정규화는 기존값을 최댓값으로 나누어 진행했다. 이때 오차가 생길 확률인 유의 수준은 0.05를 사용하였으며 이를 통해 결정된 요인의 효과 크기는 2.015로 설정하였다. X = 2.015그래프를 기준선으로 넘지 못하는 값은 통계적으로 유의미하지 못한 값으로 판단하여 스크리닝(Screening)을 통해 제거 후 반응표면법을 진행하였다. 민감도 분석 결과 설계변수 X3의 영향이 31.6%로 가장 크게 나타났으며, X1×X2, X1×X3, X1×X4 그리고 X2×X4의 변수가 유의미한 기준을 만족하지 못하였다. 따라서 앞선 4가지 변수를 제거하고 반응표면법을 진행하였다.

Table 3

Design of experiment (DOE)

2.4 반응표면법

민감도 분석을 바탕으로 설계변수들이 목적함수에 영향을 주는 것을 확인했고 이를 통해 목적함수와 설계변수들의 함수적인 관련성을 알아내고자 수학적 모형을 가정하는 방법을 회귀분석(Regression Analysis)이라고 한다. 이러한 회귀 분석을 통해 설정된 설계변수 범위 내의 목적함수의 경향을 예측할 수 있다. 반응표면법(Response Surface Method, RSM)은 일반적인 선형 회귀모델보다 더 좋은 반응의 근사치를 만들기 위해 곡선 형태의 회귀모델을 도출해 오차를 줄일 수 있는 회귀분석 방법이다[12]. 본 연구에서는 앞서 설정한 설계변수를 각 X1, X2, X3, X4로 나타냈고 이를 중심 합성계획법을 통해 Full Factorial로 성형해석을 진행했으며 Table 4에 나타냈다. 이를 통해 얻은 반응표면법의 회귀 모델 식(10)를 나타냈다.

$\[ Y=\begin{array}{l}1.049-0.798\left(X1\right)-1.802\left(X2\right)-0.734\left(X3\right)-0.378\left(X4\right)\hfill \\ +0.512\left(X1\mathrm{*}X1\right)+1.082\left(X2\mathrm{*}X2\right)+0.288\left(X3\mathrm{*}X3\right)\hfill \\ +0.243\left(X4\mathrm{*}X4\right)+0.830\left(X2\mathrm{*}X3\right)+0.557\left(X3\mathrm{*}X4\right)\hfill \end{array} \]$

(10)

Table 4

Comparison of simulation and RSM

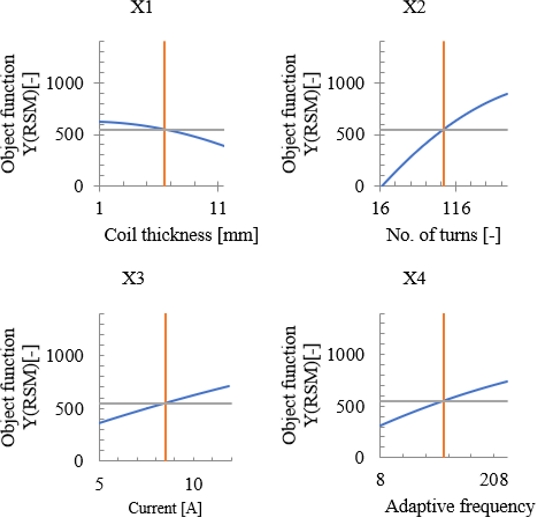
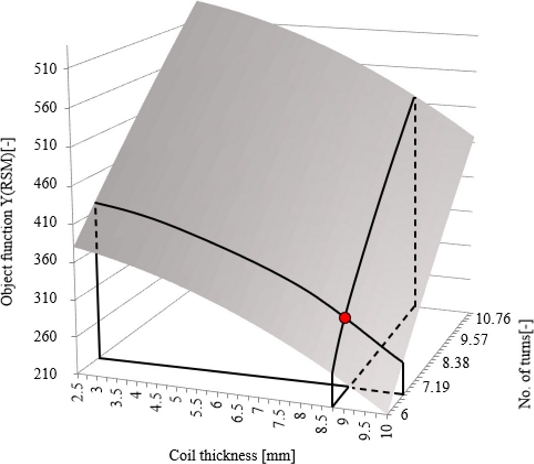
해당 예측 식의 타당성을 검토하고자 결정계수를 사용하였다. 결정계수는 0-100%의 값을 나타내며 100%에 가까워질수록 예측함수의 결과가 유효함을 뜻한다. 본 연구에서 97.85%로 회귀식의 일반적인 신뢰성 기준인 97% 이상을 만족한다[13]. 예측식을 바탕으로 각 변수의 목적함수에 대한 반응을 2D 그래프를 작성하여 Fig. 4에 나타내었다. 이를 통해 X1은 Y1에 반비례하는 경향을 보이며 X2, X3그리고 X4는 Y1에 비례하는 경향을 보이는 것을 확인하였다. 앞선 결과들을 통해 변수들과 Y1간 관계를 3차원 그래프로 작성하였으며 Fig. 4에 나타내었고 Y1과 각 변수의 관계를 통해 목적함수에 부합하는 최적 설계변수를 Table 5 정리하였다.

Fig. 3

Relationship between object function and design variable

Fig. 4

Relationship between coil thickness and no. of turns

Table 5

Optimized design variables

2.5 전자기장-열 연성 해석

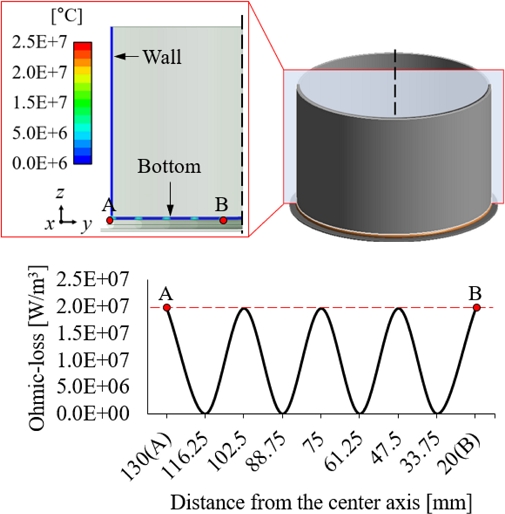
앞서 도출한 변수 Table 5를 바탕으로 전자기장-열 해석을 진행하였다. 먼저 전자기장 유한요소 해석 프로그램인 ANSYS Maxwell을 이용해 저항 손실을 계산하였으며 이를 입력 데이터로 열 유한요소 해석 프로그램 ANSYS Icepak에서 용기의 온도를 구하였다[14]. 우선 진행한 전자기장 해석 결과는 Fig. 5에 나타내었다. 각 코일에서 발생한 자기장으로 인해 저항 손실 영역이 발생한다. 이는 Fig. 5와 같이 최대 2.76E+7 W/m³의 저항 손실이 발생하였다. 코일에 가까울수록 높은 손실률을 보였으며 표면에서 멀어질수록 손실률이 낮아지는 값을 나타냈다. 이는 2.1에서 언급한 표피효과로 인해 발생한 경향으로 판단된다. 또한 Fig. 5 하단 그래프에서 나타내듯 모든 코일과 접촉되는 면의 최대 저항 손실률은 모두 동일한 값으로 나타났다.

Fig. 5

Temperature distribution of FE result and ohmic loss according to distance from the center axis

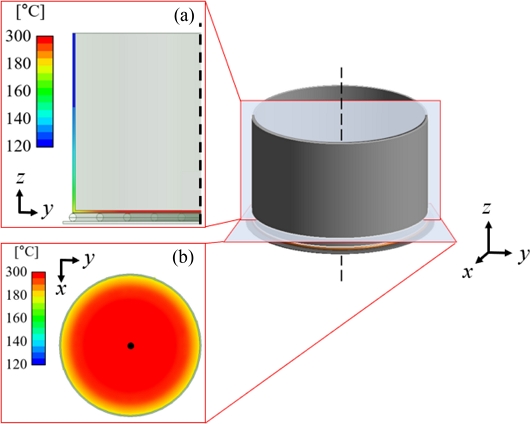
저항 손실은 식(7)과 같이 전기에너지가 열에너지로 치환되어 열이 발생하게 된다. 따라서 앞선 저항 손실 값을 입력데이터로 활용하여 열 해석을 진행하였고 해당 결과를 Fig. 6에 나타내었다. 열 해석 결과 그릇의 하단부에서 최대 299.8^oC가 나타났다. 이는 용기의 내열 온도인 300^oC와 0.07% 차이로 근사하다. 온도의 분포 경향은 Figs. 6(a)와 6(b)와 같이 하단부에서 상단부로 갈수록 중심에서 바깥으로 갈수록 온도가 점진적으로 감소하는 경향을 보였다. 이는 저항 손실영역이 가장 많이 중첩되는 곳이 하단부 중앙이기 때문에 발생한 경향으로 판단된다. 본 연구를 통해 IH 전기레인지용 내열 온도 내에서 최대 온도가 발생하는 코일의 형상 및 경계 조건이 제시되었다.

Fig. 6

Optimization result of pot’s temperature (a)wall (b)bottom

3. 결론

본 연구에서는 반응표면법을 통해 상용 스테인리스 용기가 견딜 수 있는 최적의 가열 코일 형태와 코일 수를 설계하였다. 또한 설계한 코일을 검증하기 위해 가열 프로세스를 전자기장-열 연성 해석을 통해 구현하였다.

1) 구리선의 두께, 권선 수, 인가전압 및 주파수가 코일을 통해 가열된 용기 온도에 주는 영향도를 파악하였으며 이를 통해 가열 코일은 인가전압의 영향을 가장 크게 받음을 확인하였다.

2) 민감도 해석으로부터 설계변수를 선정하고, 상용 스테인리스 용기의 내열 온도를 목표로 삼아 반응 표면법을 진행하였다. 그 결과 구리선 두께 7.2 mm, 권선 수 5개인 코일에 118.5 A, 33. 9 kHz를 인가하는 것이 최적의 조건으로 도출되었다.

3) 최적의 코일의 형태 및 조건으로 전자기장-열 연성 해석을 수행하였다. 해석 결과 내열 온도와 0.07% 차이로 근사했다. 따라서 제품 설계 시, 제한된 프로세스를 통해 시뮬레이션으로 최적의 코일 형태와 조건을 구축할 수 있을 것으로 기대된다.

REFERENCES

• Sweeney, M., Dols, J., Fortenbery, B., Sharp, F., (2014), Induction cooking technology design and assessment, Small, 800(5).
• Kim, M. J., Um, D. Y., Lee, H. Y., Kang, D. H., Park, G. S., (2021), A study on the All-Metal Induction Range in Home application, Proceedings of the Korean Institute of Electrical Engineers Conference, 142-144.
• Im, S. H., (2021), A Study on the effect of the component of induction range, Proceedings of the Korean Institute of Electrical Engineers Conference, 162-163.
• Mitsuri Media, Experts explain the heat resistance temperature of stainless steel by type. https://mitsu-ri.net/articles/stainless-steel-heat-resistant-temperature
• Ansys, ANSYS Innovation courses Maxwell. https://courses.ANSYS.com/
• Sohn, D.-H., Seo, Y.-S., Park, K., (2010), Three-dimensional finite element analysis of the induction heating procedure of an injection mold, Transactions of Materials Processing, 19(3), 152-159. [https://doi.org/10.5228/KSPP.2010.19.3.152]
• Kim, S. M., Moon, J. I., Cho, I. K., Yoon, J. H., Byun, W. J., (2014), The technical trend and future direction of wireless power transmission, Electronics and Telecommunications Trends, 29(3), 98-106.
• Material property data for engineering materials. https://www.ansys.com/content/dam/amp/2021/august/webpage-requests/education-resources-dam-upload-batch-2/material-property-data-for-eng-materials-BOKENGEN21.pdf
• Lee, I., Tak, S., Pack, I., Lee, S., (2017), Comparative study on numerical analysis using co-simulation and experimental results for high frequency induction heating on SCM440 round bar, Journal of Aerospace System Engineering, 11(3), 1-7.
• Ku, B.-M., Kim, T.-H., Park, J.-S., (2021), Determination of the temperature coefficient of the constitutive equation using the response-surface method to predict the cutting force, Journal of the Korean Society of Manufacturing Process Engineers, 20(10), 9-18. [https://doi.org/10.14775/ksmpe.2021.20.10.009]
• Lee, C., Hong, S., (2018), Curvature area prediction for the deep drawing-ironing process of a cylindrical cup using finite element method and regression analysis, Journal of Mechanical Science and Technology, 32, 5913-5918. [https://doi.org/10.1007/s12206-018-1142-4]
• Gu, B.-J., Hong, S.-M., (2019), Numerical approach to optimize piercing punch and die shape in hub clutch product, Journal of the Korea Academia-Industrial Cooperation Society, 20(9), 517-524.
• George, D., Mallery, P., (2003), SPSS for Windows step by step: A simple guide and reference. 11.0 update (4th Ed.). Boston: Allyn & Bacon.
• Ansys, ANSYS Innovation courses Icepak, https://courses.ANSYS.com/