폴리머 결찰 클립의 강성인자 해석

1. 서론

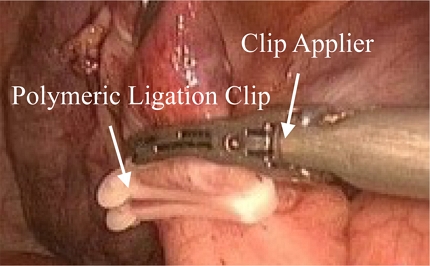
복강경을 이용한 수술은 최근 의료기기의 급속한 발달과 외과의사의 경험 축적 등으로 점차 수술 범위가 확대되고 이용빈도도 늘어나고 있다[1]. 복강경 수술에서 지혈 방식으로 최근 Fig. 1과 같이 결찰 클립(Ligation Clip)을 활용한 방식이 많이 연구되고 있다. 기존 지혈 방식과 결찰 클립 방식을 서로 비교하여 장단점을 평가하거나[2,3], 결찰 클립 방식의 유용성, 이점 등을 평가하는 연구가 이루어지고 있다[4,5]. 또한 클립용 기구의 구조 개선에 관한 연구가 제시되었다[6].

Fig. 1

Polymeric ligation clips applied by clip applier [4] (Adapted from Ref. 4 on the basis of OA)

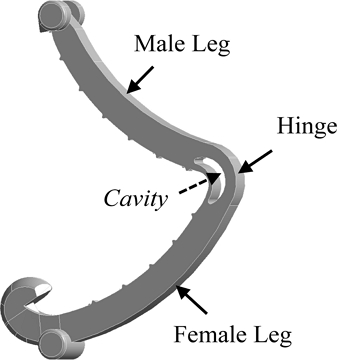
폴리머 결찰 클립은 사출을 통해 제작되며 그 형상은 Fig. 2와 같다. 클립용 기구(Clip Applier)를 이용하여 힌지(Hinge)를 굽혀서 수레그(Male Leg)가 암레그(Female Leg)에 결찰되도록 하는 구조이다. 이때 굽힘을 원활하게 하기 위해 힌지에는 공동(Cavity)을 두고 있다.

Fig. 2

Structure of polymeric ligation clip

클립용 기구는 수동형과 자동형으로 나뉜다. 수동형은 먼저 외부에서 클립을 기구 끝에 끼운 후 복강경 홀을 통해 삽입하여 결찰하는 방식으로 매 클립마다 기구를 넣었다 빼기를 반복해야 하는 번거로움이 있다. 이에 반해 자동형은 Fig. 3과 같이 클립들이 기구의 가이드 내에 미리 내장된 채 하나씩 밀어서 사용하기 때문에 수동형의 문제점인 반복 작업을 크게 줄일 수 있다. 다만, 내장된 클립이 기구 끝에 있는 죠(Jaw)에 장전될 때 수레그와 암레그가 충분히 잘 벌어져야 제 기능을 발휘할 수 있기에, 이 특성을 대표하는 폴리머 결찰 클립의 스프링상수 값이 충분히 높아야 할 필요가 있다. 이 특성은 또한 클립용 기구 제품의 유통기한과도 직결된다. 폴리머 결찰 클립은 내장된 채로 오랫동안 보관되면 응력이완(Stress Relaxation) 현상으로 인해 클립의 탄성 특성을 점차 잃기 때문이다.

Fig. 3

Automatic clip applier with built-in polymeric ligation clips [7] (Adapted from Ref. 7 on the basis of OA)

이에 따라 본 연구에서는 폴리머 결찰 클립의 스프링상수 값을 최대화하기 위해 유한요소해석을 통한 스프링상수 값 계산 및 다꾸치 최적화(망대특성)를 실시한다. 이를 통해 개선된 모델을 제시한다.

2. 연구 방법

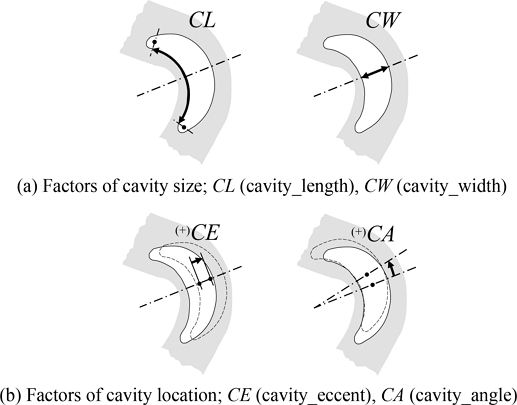
폴리머 결찰 클립은 기능적 특성상 힌지를 중심으로 탄성변형하도록 설계되었다. 수레그와 암레그의 변형은 이에 비해 매우 작으므로 무시할 수 있다. 따라서 폴리머 결찰 클립의 탄성적 특성은 힌지, 그중에서도 힌지 내 공동의 모양과 위치에서 나온다고 할 수 있다. 이에 따라 폴리머 결찰 클립의 스프링상수 값을 결정하는 요인으로 Fig. 4에 나타낸 것처럼 공동의 크기와 관련된 두 개의 인자(공동 길이 CL, 공동 폭 CW)와 공동의 위치와 관련된 두 개의 인자(공동 편심 CE, 공동 각 CA)를 선정하였다.

Fig. 4

Four design factors related to cavity size and location

폴리머 결찰 클립의 스프링상수 값은 이러한 네 개의 설계인자에 의해 통합적으로 결정되는 값이다. 통합적 평가를 위해 실험계획법 중 하나인 다꾸치법을 활용하면 스프링상수 값에 대한 인자들 간 기여도를 평가할 수 있어 매우 유용하다[8].

네 개의 인자별로 각각 세 개의 수준(Level)을 Table 1과 같이 선정하였다. 수준 2 조합이 원래 모델을 나타낸다. 각 수준은 수준 2의 값을 기준으로 힌지 기능에 문제가 없고 제작이 가능한 범위 내로 설정하였다.

Table 1

Design factors and their levels used in Taguchi method

인자 평가에는 다꾸치 직교 테이블 L18을 사용한다. L18을 사용하면 Table 1의 네 가지 설계인자의 각 세 가지 수준으로부터 총 열 여덟 가지의 공동(Cavity) 디자인을 도출할 수 있다. 각각의 공동 디자인이 반영된 폴리머 결찰 클립 형상을 생성한 후 이를 유한요소해석 상용 코드인 Ansys를 활용하여 탄성변형 해석을 실시한다. 이를 통해 폴리머 결찰 클립이 가이드에 내장된 위치에 있을 때의 스프링상수 값을 최종적으로 구할 수 있다.

해석 과정은 다음과 같다. 네 가지 인자가 모두 수준 1의 값을 가지는 경우를 예로 든다. Fig. 5는 그러한 공동 형상을 가진 클립의 유한요소 메시 모델과 적용된 경계조건을 보여준다.

Fig. 5

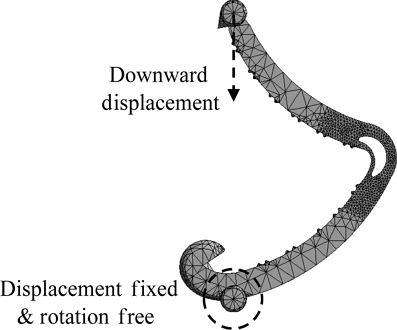
Finite element mesh model of a clip with all four factors set to level-1 and applied boundary conditions

유한요소 절점 수는 56,711개, 요소 수는 36,677개이다. 공동을 포함하는 힌지에 유한 요소를 매우 조밀하게 배치하여 해석의 정확도를 기하였다.

경계조건으로 하단부 암레그 머리에는 변위는 고정하되 회전은 자유롭도록 설정하고 상단부 수레그 머리에는 아래 방향 변위(최대 7.2 mm)를 가하였다.

폴리머 결찰 클립은 폴리머의 한 종류인 POM (PolyOxyMethylene) 재질로 만들어지며 그 물성치는 Table 2와 같다.

Table 2

Material property of POM (PolyOxyMethylene) [9] (Adapted from Ref. 9 on the basis of OA)

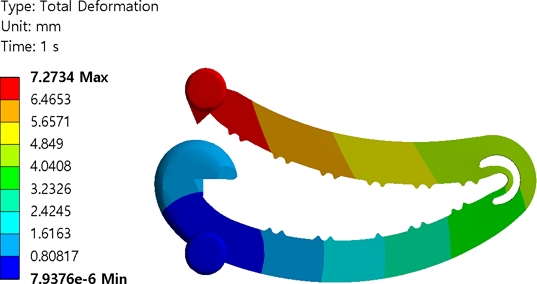
Fig. 6은 최대 변위가 가해졌을 때의 클립의 변형 형상을 보여주고 있다. 힌지 중심으로 변형이 일어남을 알 수 있다.

Fig. 6

Deformation shape of the clip by a displacement of 7.2 mm

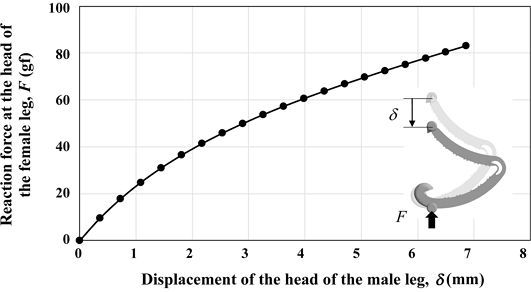
암레그 머리의 변위에 따른 수레그 머리 고정부의 반력을 Fig. 7에 나타내었다. 변형이 진행될수록 클립의 반력의 증가폭이 줄어들고 있어 비선형적 탄성 특성이 나타나는 것을 알 수 있다. 이로부터 매 순간의 스프링상수 값 k는

Fig. 7

Reaction force (F) vs. displacement (δ) of the clip

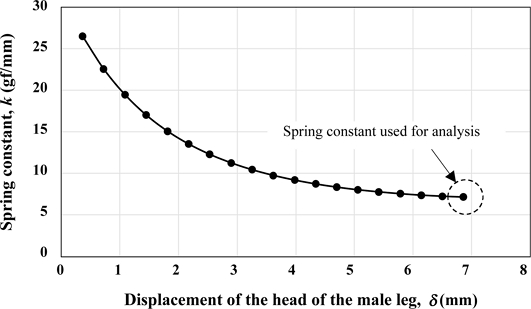
식(1)로 계산할 수 있으며 그 결과를 Fig. 8에 나타내었다. 스프링상수 값은 클립이 변형될수록 줄어들며 특정 값에 수렴함을 알 수 있다. 클립이 내장된 상태에서의 스프링상수 값은 최종값이다. 본 해석 예에서는 k = 7.195 gf/mm이다. 이 값을 다꾸치 최적화 분석에 사용한다.

Fig. 8

Spring constant (k) vs. displacement (δ) of the clip

3. 결과 및 토의

다꾸치 직교 테이블 L18의 인자 배치에 따른 열 여덟 가지 해석 조건에 따른 최종 스프링상수 값을 Table 3에 나타내었다. 앞선 예는 해석번호 1번에 해당한다. 전체적으로 설계인자 변동에 따른 스프링상수 값의 범위는 2.8-7.2 gf/mm로 나타났다.

Table 3

Spring constant by means of Taguchi method L18

네 가지 설계인자가 스프링상수 값 변화에 어느 정도로 기여하고 민감하게 변화하는지 확인하기 위하여 해석 결과에 대해 분산분석 및 평균분석을 실시하였다. 분산분석을 통해서는 스프링상수 값에 가장 기여하는 인자와 그 기여 정도를 파악할 수 있고 평균분석을 통해서는 인자의 변동에 따른 스프링상수 값 변동의 민감도를 평가할 수 있다[8].

스프링상수 값 해석 결과에 따른 분산분석 결과를 Table 4에 나타내었다. 수정된 제곱합(Adj. SS)을 보면 네 가지 설계인자 전체는 스프링상수 값 전체 변동의 약 93.5%를 대표하고 있음을 알 수 있다. 이것은 네 가지 설계인자가 잘 선택된 인자들임을 말해준다.

Table 4

Analysis of variance (ANOVA) of each design factor

유의 확률 p<0.05를 기준으로 했을 때, 공동 폭(CW)과 공동 편심(CE) 설계인자가 유의미한 것으로 나타났다. 특히, 공동 폭 인자는 전체 변동의 70.8%를 대표하는 매우 중요하고 결정적인 인자임을 알 수 있다. 공동 편심 인자는 그 다음으로서 전체 변동의 14.4%를 대표하고 있다. 이에 비해 공동 길이(CL)와 공동 각(CA) 설계인자는 스프링상수 값에 큰 영향을 주지 않는 것으로 나타났다.

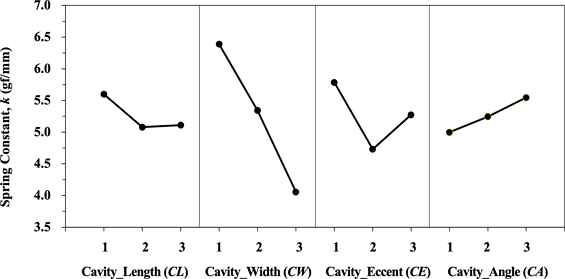
설계 인자별로 수준 변화에 따른 스프링상수 값에 대한 평균 분석을 실시한 결과를 Fig. 9에 보였다. 분산분석 결과에서 논의된 바와 같이 공동 폭의 수준 변화에 따라 스프링상수 값이 매우 민감하게 변하고 있음을 볼 수 있다. 이에 비해 공동 길이와 공동 각에 의해서는 크게 민감하지 않다. 다만 공동 각에 의한 변화량이 각도가 증가할수록 커지는 경향이라는 점은 참고할 만하다.

Fig. 9

Main effect plot about spring constant k

Fig. 9로부터 스프링상수 값을 가장 크게 만드는 설계인자 조합은 CL-1, CW-1, CE-1, CA-3 임을 알 수 있다. 이로부터 개선된 해석모델을 만들어 확인 해석을 수행한 결과를 원래 모델의 결과와 비교하여 Table 5에 나타내었다. 개선된 모델은 스프링상수 값이 55.4% 증가하였고 이로부터 다꾸치법에 의한 최적화 수행이 잘 이루어졌음을 알 수 있다.

Table 5

Increase of spring constant by the improved combination

4. 결론

폴리머 결찰 클립이 높은 스프링상수 값을 갖도록 형상 디자인을 개선하는 과정에서 클립 힌지의 공동 형상에 관한 네 가지 설계인자가 스프링상수 값에 미치는 영향을 평가하여 다음의 결론을 도출하였다.

네 가지 설계 인자(공동 길이, 공동 폭, 공동 편심, 공동 각)는 스프링상수 값 변동의 93.5%를 대표함으로써 주요 인자임이 확인되었다.

공동 폭과 공동 편심 설계인자는 유의확률 0.05를 기준으로 각각 스프링상수 값 변동의 70.8, 14.4%를 대표하면서 유의미하였으며, 특히 공동 폭 설계인자가 결정적인 인자임을 알 수 있었다.

스프링상수 값을 가장 크게 만드는 조합으로 설계된 개선 모델은 기존 모델 대비 스프링상수 값이 55.4% 증가하였다.

Acknowledgments

본 과제(결과물)은 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 3단계 산학연협력 선도대학 육성사업(LINC3.0)의 연구 결과입니다(No. 1345356224).

REFERENCES

• Kim, K.-A., Kim, Y.-K., (2004), The effects of semi-Fowler’s position on post-operative recovery in recovery room for patients with laparoscopic abdominal surgery, Journal of the Korean Society of Adult Nursing, 16(4), 566-574.
• Elgendy, A., Khirallah, M. G., (2019), Hem-o-lok clip versus hand-made loop in base closure during laparoscopic appendectomy in children, Journal of Pediatric Endoscopic Surgery, 1(3), 127-132. [https://doi.org/10.1007/s42804-019-00018-9]
• Lucchi, A., Berti, P., Grassia, M., Siani, L. M., Gabbianelli, C., Garulli, G., (2017), Laparoscopic appendectomy: Hem-o-lok versus endoloop in stump closure, Updates in Surgery, 69(1), 61-65. [https://doi.org/10.1007/s13304-016-0413-9]
• Hue, C. S., Kim, J. S., Kim, K. H., Nam, S. H., Kim, K. W., (2013), The usefulness and safety of Hem-o-lok clips for the closure of appendicular stump during laparoscopic appendectomy, Journal of the Korean Surgical Society, 84(1), 27-32. [https://doi.org/10.4174/jkss.2013.84.1.27]
• Soll, C., Wyss, P., Gelpke, H., Raptis, D. A., Breitenstein, S., (2016), Appendiceal stump closure using polymeric clips reduces intra-abdominal abscesses, Langenbeck’s Archives of Surgery, 401(5), 661-666. [https://doi.org/10.1007/s00423-016-1459-3]
• Han, S. H., Choi, B. L., (2023), A Study on the structural improvement of ligation parts of a polymer clip blood vessel ligator, Journal of the Korean Society for Precision Engineering, 40(8), 593-598. [https://doi.org/10.7736/JKSPE.023.027]
• Teleflex, Weck Auto Endo5 Automatic Clip Applier, https://www.teleflex.com/sea/en/product-areas/surgery/
• Lee, S.-W., Ko, C.-W., (2023), A study on the design factors of contact pressure by femur fixation grip made of shape memory alloy used for human femoral fracture, Journal of the Korea Academia-industrial Cooperation Society, 24(1), 290-296. [https://doi.org/10.5762/KAIS.2023.24.1.290]
• SAM HWA, POM (Acetal), http://www.wangkang.kr/bs/?subAct=view&bid=PRODUCT&seq=16