폴리아세탈 수지의 건식 인덱서블드릴 가공에서 가공오차 감소를 위한 최적조건 선정


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, polyacetal plates were machined with an indexable drill (Ø18mm) to measure the dimensional error of holes according to the cutting conditions and investigate the influencing factors to obtain precision holes. Cutting velocity, feed, and depth of cut were selected as experimental variables, analyzed using design of experiment, and optimal cutting conditions were investigated. Cutting velocity and feed were significant factors affecting hole accuracy, whereas depth of cut had little effect. The factor with the greatest influence on hole accuracy was cutting velocity, and the dimensional error of the holes tended to increase as the cutting velocity increased. Dimensional error tended to decrease as feed increased. In addition, the interaction effect between cutting velocity and feed and cutting velocity and depth of cut were significant. In this experiment, the optimal cutting velocity, feed, and depth of cut needed to minimize the dimensional error of holes were 100 m/min, 0.15 mm/rev, and 2 mm, respectively.
Keywords:
Polyacetal, Indexible drill, Hole accuracy, Design of experiment키워드:
폴리아세탈, 인덱서블 드릴, 구멍 정밀도, 실험 계획법1. 서론
산업용 플라스틱은 강도와 탄성이 좋으며 내충격성, 내열성, 내식성 등 우수한 기계적, 화학적 성질을 바탕으로 자동차, 항공기, 의료기기, 전자부품 등 산업 전반에 적용되고 있다. 더불어 생산성, 조형성 등 산업용 플라스틱의 장점을 바탕으로 사용량은 철강을 이미 넘어섰고 지속적으로 증가하고 있는 추세이다[1]. 산업용 플라스틱은 재료가 지닌 열적, 유변적 특성을 이용한 사출, 압출 등의 공정으로 대량생산 하는 방식이 일반적이었으나 최근 정밀기계, 광학 부품 등의 수요가 증가하며 절삭가공의 필요성과 중요성이 높아지고 있다[1-9]. 더불어 최근 다품종 소량 생산에 대한 요구와 함께 복잡한 형상에 대한 금형 비용 상승 등으로 산업용 플라스틱에 대한 절삭가공 연구의 필요성이 증가하는 실정이다[11,12]. 이러한 산업계의 요구로 산업용 플라스틱의 절삭가공에 관한 연구가 최근까지 활발히 진행되고 있다[10-14].
Xiao 등은 플라스틱의 선삭가공 시 점성변형(Viscous Deformation) 특성이 표면품위를 결정짓는 데 결정적인 역할을 한다고 하였다. 선삭가공 시 점성변형에 의한 표면뜯김을 방지하기 위해서는 절삭유 공급을 통한 냉각으로 소성변형을 억제할 필요가 있다고 하였다[3]. Davim 등은 산업용 플라스틱의 선삭가공 시 공구의 재종이 가공품질에 미치는 영향에 대해 연구하였다. 실험 결과 동일한 절삭조건에서 소요 동력, 비절삭저항 지표에서는 공구재종 변화가 유의미한 차이를 보이지 않았으나, 표면거칠기 값에서는 초경(Tungsten Carbide)에 비해 PCD (Polycrystalline Diamond) 재종으로 실험한 시편이 낮은 측정값을 보였다고 하였다[4]. Fetecau 등은 산업용 플라스틱의 선삭가공 시 절삭조건 변화에 따른 표면거칠기, 온도, 그리고 절삭력 변화에 관해 실험하였다. 그 결과 절삭 속도와 이송량이 증가할수록 절삭력 역시 증가하며, 절삭 속도는 온도변화에 미치는 주효한 인자라는 것을 밝혔다. 그리고 절삭 속도가 증가함에 따라 표면품위는 개선되었다고 하였다[6]. 선삭가공에 이어 산업용 플라스틱의 1 mm 이하 소구경 드릴가공에 관한 연구에서는 절삭조건 변화 시 구멍의 정밀도에 미치는 영향에 대해 실험하고 분석하였다. 분석결과 이송량이 낮고 회전수가 높은 경우 구멍의 정밀도는 낮아지며 드릴의 회전당 이송(Feed Rate per Unit Drill Rotation)이 구멍의 정밀도에 영향을 미치고 낮을수록 정밀도가 낮아진다고 밝혔다[5]. 이는 Davim 등의 연구 결과에서 회전당 이송량이 증가함에 따라 비절삭저항이 낮아졌다는 결론을 통해 드릴가공에서도 낮은 이송조건에서 비절삭저항이 상대적으로 증가하여 구멍의 정밀도가 낮아졌다고 추론해볼 수 있다[4]. 다음으로 Palanikuma는 엔지니어링 플라스틱의 일종인 GFRP (Glass Fibre-reinforced Polymer)의 드릴가공 시 절삭조건의 영향력을 다구찌방법(Taguchi Method)을 활용하여 정량적으로 분석하였다. 분석결과 주축 회전수와 이송량 사이에는 교호 효과(Interaction Effect)가 있으며 높은 주축 회전수와 낮은 이송조건에서 더욱 두드러진다고 하였다[9]. 이와 더불어 Ramesh 등의 연구에서는 다구찌방법을 적용하여 GFRP의 드릴가공 시 주축회전수와 이송량이 가공오차에 미치는 영향을 분석하였다. 연구결과에서 주축의 회전수가 증가함에 따라 가공오차가 증가하는 반면 이송량이 증가하면 가공오차가 감소하는 결과를 보였다고 하였다[10]. 이는 앞서 언급된 Endo 등의 연구와 비교해 볼 때 유사한 결과이며 주축 회전수와 이송이 가공오차를 결정짓는 주요 변수임을 알 수 있다[5]. 구멍 가공에 관한 비교적 최근 연구를 살펴보면 Uysal 등은 산업용 플라스틱의 드릴가공 시 가공조건이 구멍정밀도에 미치는 영향을 파악하기 위해 폴리아세탈(Polyacetal)과 캐스트폴리아미드(Cast Polyamide)를 피삭재로 선정하여 실험을 수행하였다. 연구 결과에서 주축 회전수와 이송량이 증가함에 따라 구멍의 정밀도가 낮아졌지만, 폴리아세탈의 경우 높은 주축 회전수에서 이송량의 증가에 따라 반대로 오차가 감소한다고 하였다[12]. 이는 이전 Palanikuma의 연구에서 밝힌 바와 같이 폴리아세탈 가공에서도 변수 간에 교호 효과가 있으며 드릴의 이송량이 구멍의 정밀도에 영향을 미친다는 Davim 등과 Endo 등의 선행 연구 결과와도 유사한 결론이다[4,5,9]. 이와 더불어 Susac 등은 폴리아세탈, 폴리아미드, 그리고 폴리에틸렌(Polyethylene) 수지의 구멍 가공성을 파악하기 위해 실험계획법을 활용하여 각종 절삭변수와 구멍 가공성 간의 관계를 정량적으로 분석하였다. 실험 결과 구멍의 진원도 오차에 유의한 영향을 미치는 인자는 드릴의 직경, 즉 공구의 강성이 주된 인자이고 주축의 회전수 및 이송량은 종속변수에 미치는 영향력이 미미하다고 하였다[13]. 그러나 이는 드릴의 강성이 종속변수에 미치는 영향력이 매우 커서 나머지 변수의 영향력이 상대적으로 작게 검출된 것이라 판단된다.
선행연구를 기반으로 본 연구에서는 비교적 대구경 인서트 교환형 드릴(Indexible Drill)을 이용하여 연구를 수행하였다. 1 mm 이하 드릴가공 중심의 기존 연구와 차별하여 대구경 드릴 가공에 관한 연구가 필요할 것으로 판단된다. 특히 절삭 속도와 이송량과 더불어 이전 드릴가공에 관한 연구에서 반영하지 않았던 절입깊이의 영향도 함께 분석하였다. 이를 위해 산업용 플라스틱으로 널리 활용되는 폴리아세탈을 선정하여 실험계획법(Design of Experiment)을 통해 실험설계 및 결과분석, 그리고 최적 조건을 도출하였다.
2. 실험설계 및 방법
2.1 실험설계
본 실험에서는 종속변수에 영향을 주는 유의한 인자 선별과 최적 조건, 그리고 교호 효과까지 검출하기 위해 완전요인계획법(Full Factorial Design)에 의한 실험을 설계하였고 절삭 속도, 이송, 그리고 절입깊이의 3인자, 3수준으로 설계하였다. 각기 다른 조건으로 총 27회의 실험을 통해 종속변수와의 관계를 파악하고자 하였다. 종속변수는 공구 직경 대비 구멍의 오차를 분석하고자 선행연구를 바탕으로 식(1)과 같이 정의하였다[9-12].
| (1) |
| (2) |
측정된 결괏값은 식(2)와 같이 망소특성(Smaller the Better Characteristics)을 적용하였는데 이는 종속변수의 특성상 작을수록 생산공정에 적합하기 때문이며 진동, 공구수명 등 잡음에 대한 신호의 선명도를 나타내고자 하였다. 각 실험변수에 따른 수준 및 조건은 Table 1과 같다. 모든 조건은 예비실험을 통해 안정적인 절삭이 가능한 영역 내에서 선정하였고 수준별 간격을 동일하게 하여 수준 변화에 따른 종속변수의 거동을 직관적으로 파악할 수 있도록 설계하였다. 그리고 이송의 최소값(0.05 mm/rev)은 인선부 형상(Edge Preparation)을 고려하여 적정 미변형칩두께(Undeformed Chip Thickness)를 유지하여 급격한 절삭 부하 상승과 이로 인한 진동을 방지하기 위함이다.
2.2 실험방법
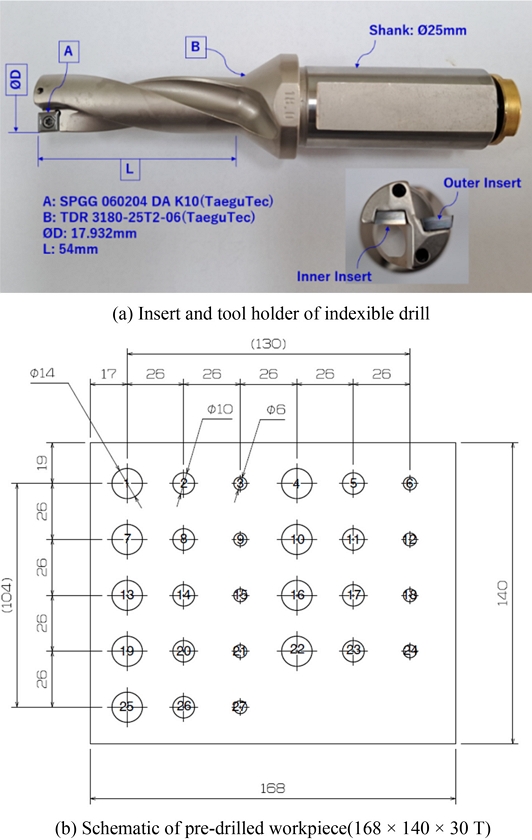
Table 2에서는 본 실험에 사용된 폴리아세탈 수지의 기계적 성질을 나타낸 것이다. 본 실험을 위해 사용된 공구(Fig. 1(a))는 몸체를 구성하는 툴홀더(Tool Holder)와 절삭인선 부분인 인서트(Insert)로 구분된다. 또한 외측 인서트 1개, 내측 인서트 1개가 조합하여 전체 1날을 구성한다. 인서트는 초경재질의 코팅되지 않은 재종을 선택하였는데 Table 2에 나타낸 재료의 기계적 성질을 바탕으로 추론해볼 때 공구의 마모가 구멍 오차에 미치는 영향이 비교적 낮을 것이라 판단되었고 코팅된 인선에 비해 코팅되지 않은 인선의 경우 예리한 공구 날 끝을 형성할 수 있기 때문이다.
이송은 공작기계에 입력하는 테이블 이송(mm/min)이 아닌 회전당 이송(mm/rev)을 변수로 선정하였는데 이는 절삭 속도에 영향을 미치는 회전수(RPM)와 독립적으로 조건을 부여하기 위함이다. 그리고 절입깊이 변수의 영향을 파악하기 위해 Fig. 1(b)와 같이 예비 가공으로 실험조건에 따른 기초 구멍 가공을 미리 수행하였다. 이는 공차수준에 따라 황삭에서 정삭에 이르는 단계별 가공을 통해 요구 정도를 획득하는 일반적인 절차에 해당하며 절입깊이는 정삭 여유를 의미한다. 그리고 공작물을 탈거하지 않고 기초 구멍 가공(황삭)과 정삭이 동시에 이루어지도록 하여 위치오차를 최소화하였다.
가공된 시편은 버(Burr) 및 이물질 제거 후 3차원 측정기(CORDAX RS-50 DCC, Sheffield Measurement)를 통해 내경을 측정하였다. 측정 부분은 구멍 입구에서 15 mm 아래 부분으로 시편높이의 1/2 지점이다.
3. 결과분석
3.1 주효과 및 교호 효과 분석
측정된 자료를 바탕으로 분산분석을 실시하였고 그 결과는 Table 3과 같다. 절삭 속도(A) 및 이송(B)은 95% 신뢰수준(Significant Level) 내에서 유의한 인자인 반면 절입깊이(C)는 수준 변화에 따른 효과가 미미한 것으로 나타났다. 그리고 절삭 속도와 이송(A × B) 사이에는 교호 효과가 유의한 반면 절삭 속도와 절입깊이(A × C) 사이에는 95% 신뢰수준 내에서는 유의하지 않지만 비교적 약한 교호 효과가 검출되었다. 이는 실험 결과를 설명하는 모델링을 통해 유의성 여부를 종합적으로 추론해야 할 것으로 판단된다.
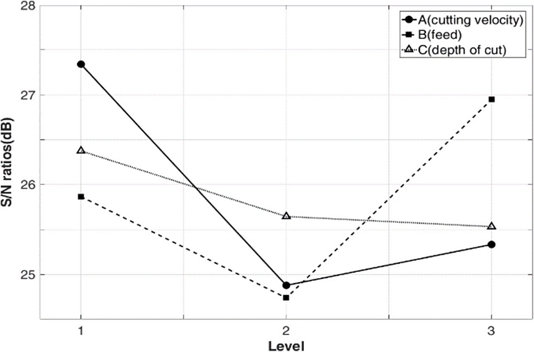
Fig. 2에서는 독립변수의 수준 변화에 따른 주 효과를 나타내었으며 절삭 속도(A)는 평균 S/N 비의 최곳값과 최젓값의 차이가 2.46 dB (= 27.34-84.88 dB) 이송(B)은 2.21 dB (= 26.95-24.74 dB), 그리고 절입깊이(C)의 경우 0.84 dB (= 26.37-25.53 dB)으로 절삭 속도가 구멍의 가공 정밀도에 가장 큰 영향을 미친다는 것을 알 수 있다.
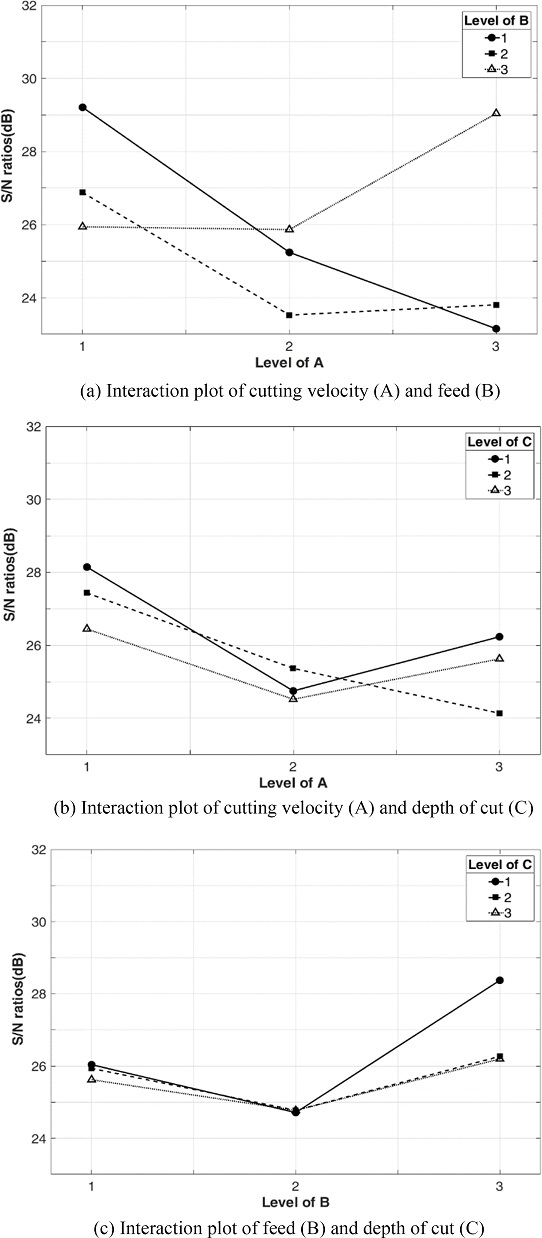
절삭 속도와 이송의 주 효과도에서 수준이 높아짐에 따라 비선형적 거동을 보이는데 이는 인자간 특정 수준에서 교호작용에 의한 결과로 판단된다. 이에 Fig. 3과 같이 교호 효과도(Interaction Plot)를 통해 인자 간 영향을 분석하였다. 절삭 속도와 이송의 경우 2수준과 3수준 사이에서 교호 효과가 검출되었으며 절삭 속도와 절입깊이 변수 간에도 동일 범위에서 교호작용에 의한 영향력이 관찰되었다. 이는 건식가공에서 절삭 속도가 상승함에 따라 절삭열이 폴리아세탈의 기계적 성질에 영향을 미쳤기 때문이라 판단된다. 더불어 이송과 절입깊이 간에는 뚜렷한 교호 효과가 관찰되지 않았는 점으로 보아 이와 같은 분석을 뒷받침할 수 있다.
3.2 모형분석
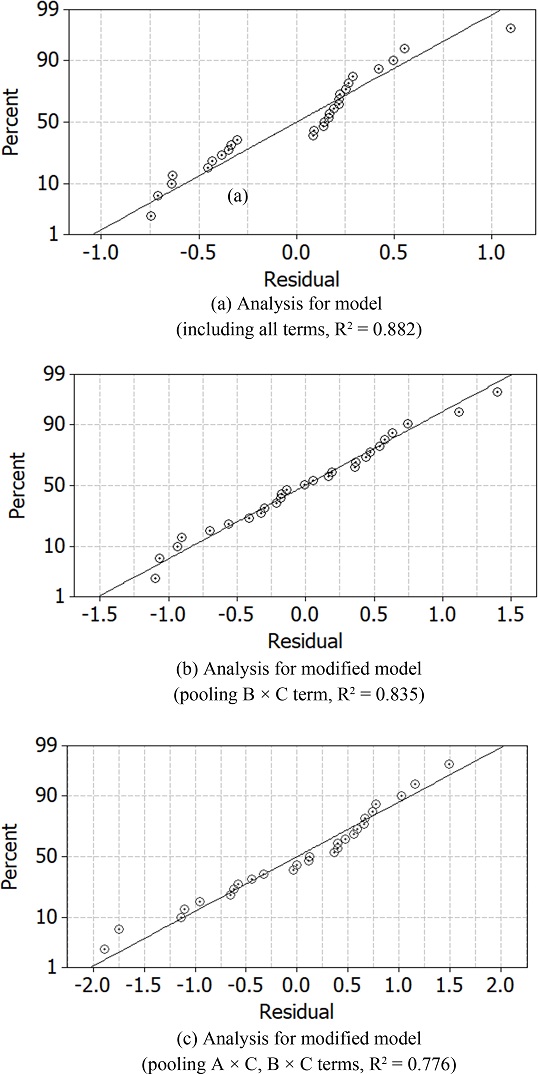
실험변수의 조합이 실험 결과를 설명할 수 있는지 확인하기 위해 3가지 모형을 구성하여 결정계수(R2)와 잔차정규확률도(Normal Probability Plot of Residuals)를 활용하여 검증하였다. 다중회귀(Multiple Regression)를 적용하여 모형을 구성하였고 각 항(Term)별 계수는 Table 4와 같다. 분산분석 결과(Table 3)를 고려하여 항의 유의도에 따라 3가지로 분류하여 분석하였다. 모든 독립변수항과 교호작용항까지 포함된 모형(Fig. 4(a))에서는 결정계수가 0.882, B × C항을 제거한 모형(Fig. 4(b))은 0.835, 그리고 A × C 및 B × C항을 제거한 모형(Fig. 4(c))은 결정계수가 0.776으로 항을 제거(Pooling)할수록 모형의 결정계수는 감소하였으나 결정계수는 상대적인 척도로 모형의 신뢰성을 판단할 수 없다. 이에 Fig. 4와 같이 잔차정규확률도를 함께 분석하였다.
B × C항을 제거한 모형(Fig. 4(b))의 잔차(Residual)가 정규확률분포에 가장 근접하였고 모든 항을 포함한 모형의 잔차가 정규확률에서 벗어나는 빈도가 높았다. 비록 B × C항을 제거한 모형이 결정계수는 모든 항을 포함한 모형보다 상대적으로 감소하였지만, 종속변수를 예측하는 예측값의 오차가 낮게 분포하였다. 이에 절삭 속도와 이송, 절입깊이(A × B, A × C)간 교호 효과는 유의한 인자이며 이송과 절입깊이(B × C)간 교호 효과는 모형에 과적합(Overfitting)을 일으켜 모형의 설명력을 저하시켰다고 볼 수 있다.
3.3 모형검증
Table 5에서는 각 모형의 신뢰성을 검증하기 위해 모형별 최적조건에서의 추정값(Estimates)을 나타내었다. 선정된 최적조건은 절삭 속도(A), 이송(B), 절입깊이(C) 변수에서 가장 높은 S/N비의 조합으로 A1B3C1 이다. 최적조건에서의 구멍 오차는 0.045 mm, S/N비는 26.936 dB로 측정되었다. 검증결과 모형 2번(Pooling B × C Term)이 측정값과 추정값의 S/N비 차이가 0.193 dB로 가장 작았으며, 모형 1번은 0.71 dB로 가장 높았다. 검증을 통해 절삭 속도와 이송 및 절입깊이 사이에는 교호 효과가 설명되며 이송과 절입깊이 간의 교호항은 예측모델의 설명력을 저하시키는 인자임을 검증할 수 있었다.
4. 결론 및 향후과제
4.1 결론
산업용 플라스틱의 구멍가공 시 정밀한 구멍을 얻기 위해 본 연구에서는 폴리아세탈 수지를 인서트 교환형 드릴을 이용하여 절삭조건별 구멍 오차를 측정하고 이에 영향을 미치는 인자를 조사하였다. 절삭 속도, 이송, 그리고 절입깊이를 실험변수로 선정하였고 각 조건에 따른 측정값을 실험계획법을 통해 정량적으로 분석하고 최적가공조건을 탐색하였다. 본 연구를 통해 다음과 같은 결론을 얻을 수 있었다.
1) 절삭 속도와 이송은 구멍 오차에 영향을 미치는 유의한 인자이다. 반면 절입깊이는 구멍 오차에 미치는 영향력이 미미하였다.
2) 구멍 오차에 가장 큰 영향을 미치는 인자는 절삭 속도며 절삭 속도가 증가함에 따라 구멍 오차는 증가하는 경향을 보인다. 반면 이송은 증가함에 따라 구멍 오차가 감소하는 경향을 보인다.
3) 절삭 속도가 상승(200 m/min 이상)하는 구간에서 이송과 절입깊이 변수의 효과에 영향을 미치는 점을 교호 효과 분석으로 파악하였다. 이는 절삭 속도가 증가함에 따라 발생하는 절삭열이 폴리아세탈 수지의 기계적성질에 영향을 미쳤기 때문이라 분석된다.
4) 본 연구에서 제시한 절삭범위에서 폴리아세탈 수지의 건식 드릴가공 시 구멍 오차를 최소화할 수 있는 최적 가공조건은 절삭 속도 100 m/min, 이송 0.15 mm/rev, 절입깊이 2 mm이다.
4.2 향후과제
본 연구에서는 직경 1 mm 이하 드릴가공 중심의 선행연구를 확장하여 직경 18 mm 인서트 교환형 인덱서블 드릴을 이용한 연구를 수행하였다. 인서트 교환형 드릴은 일체형(Solid Type) 드릴과는 제작방식, 재질, 구조, 기계적 특성 등이 다르므로 다양한 연구가 필요할 것으로 판단된다. 그리고 본 연구를 통해 폴리아세탈의 드릴가공 시 절삭 속도 200 m/min 이상의 조건에서는 가공오차 발생 경향이 변화(Fig. 3)되었음을 알 수 있는데 절삭열에 의해 절삭기구가 변화되었다고 추정된다. 이에 냉각방식, 공구의 열전도율 변화(코팅, 재종) 등 다양한 변수를 추가하여 가공오차 제어에 관한 연구가 후속된다면 엔지니어링 플라스틱 가공에 관한 지식 확장에 기여할 것으로 판단된다.
NOMENCLATURE
| ΔDi : | Dimensional Error |
| DT : | Drill Diameter |
| Di : | Hole Diameter |
| S/N : | Signal to Noise Ratio |
| n : | Number of Experiment |
| yi : | Response of Experiment |
REFERENCES
-
Alauddin, M., Choudhury, I., El Baradie, M., Hashmi, M., (1995), Plastics and their machining: a review, Journal of Materials Processing Technology, 54(1-4), 40-46.
[https://doi.org/10.1016/0924-0136(95)01917-0]

-
Zhang, H., Chen, W., Chen, D., Zhang, L., (2001), Assessment of the exit defects in carbon fibre-reinforced plastic plates caused by drilling, Key Engineering Materials, 196, 43-52.
[https://doi.org/10.4028/www.scientific.net/KEM.196.43]

-
Xiao, K., Zhang, L., (2002), The role of viscous deformation in the machining of polymers, International Journal of Mechanical Sciences, 44(11), 2317-2336.
[https://doi.org/10.1016/S0020-7403(02)00178-9]

-
Davim, J., Reis, P., (2004), Machinability study on composite (polyetheretherketone reinforced with 30% glass fibre-PEEK GF 30) using polycrystalline diamond (PCD) and cemented carbide (K20) tools, The International Journal of Advanced Manufacturing Technology, 23, 412-418.
[https://doi.org/10.1007/s00170-003-1779-7]

-
Endo, H., Marui, E., (2006), Small-hole drilling in engineering plastics sheet and its accuracy estimation, International Journal of Machine Tools and Manufacture, 46(6), 575-579.
[https://doi.org/10.1016/j.ijmachtools.2005.07.026]

-
Fetecau, C., Stan, F., Munteanu, A., Popa, V., (2008), Machining and surface integrity of polymeric materials, International Journal of Material Forming, 1, 515-518.
[https://doi.org/10.1007/s12289-008-0192-z]

-
Gaitonde, V., Karnik, S., Mata, F., Davim, J., (2008), Taguchi approach for achieving better machinability in unreinforced and reinforced polyamides, Journal of Reinforced Plastics and Composites, 27(9), 909-924.
[https://doi.org/10.1177/0731684407085875]

-
Feyzullahoglu, E., Saffak, Z., (2008), The tribological behavior of different engineering plastics under dry friction conditions, Materials & Design, 29(1), 205-211.
[https://doi.org/10.1016/j.matdes.2006.11.012]

-
Palanikumar, K., (2011), Experimental investigation and optimization in drilling of GFRP composites, Measurement, 44(10), 2138-2148.
[https://doi.org/10.1016/j.measurement.2011.07.023]

- Ramesh, B., Sharan, S. J. C., Kavialagan, R., (2013), Experimental investigation and optimization in drilling GFRP polymeric composites using Taguchi and ANOVA, International Journal of Mechanical and Production Engineering, 2(1), 52-60.
-
Altan, M., Altan, E., (2014), Investigation of burr formation and surface roughness in drilling engineering plastics, Journal of the Brazilian Society of Mechanical Sciences and Engineering, 36, 347-354.
[https://doi.org/10.1007/s40430-013-0089-8]

-
Uysal, A., Altan, M., (2018), Accuracy estimation in drilling small holes on engineering plastics by a mathematical approach, Proceedings of the Institution of Mechanical Engineers, 232(21), 3807-3813.
[https://doi.org/10.1177/0954406217742940]

-
Susac, F., Tabacaru, V., Teodor, V., Baroiu, N., (2019), Effect of cutting parameters on the hole quality in dry drilling of some thermoplastic polymers, Materiale Plastice, 56(1), 245-251.
[https://doi.org/10.37358/MP.19.1.5160]

-
Baroiu, N., Costin, G.-A., Teodor, V. G., Nedelcu, D., Tabacaru, V., (2020), Prediction of surface roughness in drilling of polymers using a geometrical model and artificial neural networks, Materiale Plastice, 57(3), 160-173.
[https://doi.org/10.37358/MP.20.3.5390]


Associate Professor, Department of Mechanical Engineering, Keimyung College University. His research interest is precision machining.
E-mail: chunsh@kmcu.ac.kr