자율주행 차량의 고속 주행 안정성 향상을 위한 곡률 기반 경로 추종 제어 알고리즘 개발 및 검증

1. Introduction

자율주행 기술과 시장이 확대됨에 따라 정확하고 안전하며, 편안한 주행 성능을 갖춘 자율주행 기술에 대한 필요성이 대두되고 있다. 자율주행 차량은 위치 파악 및 매핑, 인지, 경로 생성 및 제어와 같은 많은 기술들을 포함하고 있다[1]. 그중 경로 추종의 목표는 생성된 경로를 따라 자율주행 차량을 안내하는 적절한 조향을 입력하여 차량이 미리 정의된 경로를 따라 움직일 수 있도록 차량에 제어 명령을 입력하는 것이다[2]. 경로 추종과 같은 제어 기술은 차량 모델링에 크게 의존하기 때문에 제어설계 부분과 차량의 모델링이 일치하지 않으면 문제가 발생한다[3]. 이와 같은 문제로 인해 방향 오차와 횡방향 거리 오차의 수치가 증가하고 차선이탈, 차량 진동의 발산 및 다른 차량과 구조물 간 충돌 등 차량의 주행 불안정성을 증가시킨다. 자율주행 제어 알고리즘은 차량이 직진 구간에서 급격한 커브로 변경되는 도로 구간에서 주행 안정성이 급격하게 감소하며, 그 결과 충돌 등의 사고로 이어진다[4]. 동일한 구간에서 실제 운전자들의 경우 경로를 유지하며 전방 도로 상황을 확인하면서 적절한 조향 및 속력을 차량에 입력하며 안전하게 주행한다. 따라서 급격한 커브 구간이 존재하는 도로에서 자율주행은 실제 운전자들의 운전 성향이 고려된 주행 알고리즘으로 개발되어야 한다.

이처럼 자율주행 시스템에서 경로 추종을 위해 많은 알고리즘이 개발되었다. 그중 PID 제어는 오차를 기반으로 제어 신호를 생성하여 시스템을 원하는 상태로 만든다[5]. 자율주행에서 PID 제어는 주로 속도와 간단한 경로의 추종에 사용된다. 하지만, PID 제어는 급격한 방향 전환과 같은 복잡한 경로가 존재하는 경우에는 추종 성능이 떨어지게 된다[6]. 이러한 한계를 극복하기 위해 개발된 알고리즘 중 하나가 Pure Pursuit 알고리즘이다. 이 알고리즘은 차량이 추종해야 할 목표점을 설정하고, 이 목표점을 향해 차량을 이동시키는 방식으로 경로를 추종한다[7,8]. Pure Pursuit 알고리즘은 곡률이 존재하는 경로에서 부드럽게 추적이 가능하다는 장점이 있지만, 차량의 속도가 높아질수록 오차가 커지는 단점이 있다. 고속 경로 추종에서의 성능 문제로 인해 Stanley 알고리즘이 개발되었다. 이 알고리즘은 차량의 조향 각도를 직접 조절하여 오차를 최소화시키며[9,10], 고속 주행과 복잡한 경로 조건에서도 안정적인 성능을 보였다. 하지만, Stanley 알고리즘은 경로와 차량의 위치만을 기반으로 하기 때문에 외부 환경 변화나 차량의 동적 특성을 완벽하게 반영하기 어렵다는 한계가 존재한다. 이를 극복하기 위해 LQR 알고리즘이 개발되었다. LQR 알고리즘은 시스템의 상태를 선형으로 모델링하고, 제어 입력을 통해 상태의 차이를 최소화하여 보다 정밀한 제어가 가능하다[11]. LQR은 동적 특성과 외부 환경 변화를 모두 고려할 수 있기 때문에 다양한 시나리오에서 우수한 성능을 보인다. 이러한 경로 추종 알고리즘의 효율성과 성능을 검증하기 위해 ROS 환경에서의 CARLA Simulator를 사용하는 연구들이 증가하고 있다[12-14].

본 논문에서는 자율주행 차량의 주행 안정성 향상을 위한 경로 추종 알고리즘을 제안하였다. 차량이 직진 구간을 지나 급격한 커브 구간을 통과할 때, 커브 구간의 곡률 정보와 실제 운전자들의 운전 성향과 같이 일정한 거리의 앞부분을 주시하며 주행하기 위한 Preview Distance를 적용해 Curvature-based Feed-forward Control을 구성했다. Curvature-based Feed-forward Control을 통해 급격한 커브 구간을 빠른 속도로 통과할 때, 전방의 도로 상황을 파악하고 차량에 조향을 미리 입력 및 제어할 수 있었다. 주행 안정성 향상을 위해 Feedback Control 중 선형제어 이론을 기반으로 하는 LQR (Linear Quadratic Regulator)을 사용하였으며, Curvature-based Feed-forward Control과 Feedback (LQR) Control 출력 조향을 합산하여 자율주행 차량의 조향을 입력하였다. 제안한 경로 추종 알고리즘 검증을 위해 CARLA Simulator를 활용하였다. CARLA Simulator는 자율주행 연구를 위한 오픈소스 시뮬레이터이며, 다양한 도로환경과 교통 상황을 제공한다[15]. 사용자는 다양한 차량과 날씨를 선택하여 반복적으로 시뮬레이션을 진행할 수 있다. 이러한 기능은 자율주행 시스템의 성능과 동작을 평가하고 검증하는 데 유용하기 때문에 자동차 업계뿐만 아니라 다양한 회사와 학교 및 연구소에서 많이 사용되고 있다. 주행 경로는 CARLA Simulator에서 제공하는 맵을 사용하였으며, 완만한 커브 구간 및 급격한 커브 구간 주행을 위해 맵의 Waypoint를 사용하여 참조 경로를 생성하였다. 해당 참조 경로를 계수화하여 실제 경로로 사용하였다. CARLA Simulator의 차량 모델과 제어 알고리즘의 동역학 모델에 대한 검증을 위해 동일한 조향을 입력하였으며, 두 모델의 Side Slip Angle (β)과 Yaw-rate (γ)를 비교하는 과정을 진행하였다. 경로 추종 실험은 다양한 속력 및 곡률의 크기에 대한 방향 오차 및 횡방향 거리 오차의 수치가 최솟값으로 출력되는 최적의 가중치 행렬 Q와 상수 R 및 Preview Distance 값을 도출하기 위해 해당 값들을 조정하며 실험을 진행하였다. 오차의 최솟값 확인을 위해 RMS (Root Mean Square)를 사용하여 최적의 가중치 행렬 Q와 상수 R 및 Preview Distance에 대한 평균 오차를 구하였다. 해당 값을 적용하여 실험을 진행하였으며, 그 결과 알고리즘의 성능 및 차량의 주행 안정성을 확인할 수 있었다. 또한 Pure Pursuit과 Stanley Method를 동일한 환경에서 실험을 진행하였으며, 본 논문에서 제안하는 알고리즘과 타 추종 알고리즘을 비교하였을 때, 안정성 및 추적 성능이 높다는 것을 확인하였다. 본 논문의 구성은 다음과 같다. 2장에서는 경로 추종을 위한 차량 동역학 모델에 대해 설명한다. 3장에서는 횡방향 제어 알고리즘에 대해 설명하고, 4장에서는 시뮬레이션 실험 결과를 보여준다. 그런 다음 제안된 알고리즘의 요약 및 향후 연구를 설명하는 결론을 5장에서 다룬다.

2. State Space Model of Vehicle and Validation

2.1 Vehicle Dynamics based Error Model

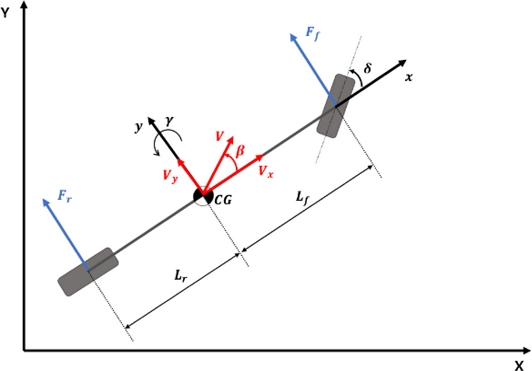
Fig. 1은 차량의 측면 동역학 모델을 나타낸다. 차량의 측면 동역학 모델은 차량의 중앙 경로와 함께 Bicycle Model과 오류 동역학 방정식을 결합하여 설계되었다[16]. Bicycle Model의 측면 동역학 모델은 Newton-euler 운동 방정식으로 무게 중심에서의 힘과 모멘트를 합산하여 아래와 같은 식(1)과 식(2)으로 표현된다.

$\[ m{a}_y=F_{yf}+F_{yr} \]$

(1)

$\[ I_z\dot{\gamma }=L_f{F}_{yf}-L_r{F}_{yr} \]$

(2)

Fig. 1

Lateral bicycle model of the vehicle for lateral dynamics

여기서 a_y는 차체 고정 좌표로 분해된 관성 기준 프레임에 대한 차량의 횡가속도이며, $$ \dot{\gamma }$$은 차량의 요각의 시간에 대한 미분이다. a_y는 아래와 같은 식(3)으로 표현된다.

$\[ a_y={\dot{V}}_y+{\dot{V}}_x\dot{\gamma }=V_x\left(\dot{\beta }+\gamma \right) \]$

(3)

여기서, V_x와 V_y는 각각 차량의 중심점에서 차량의 종방향 및 횡방향 속력을 의미하며, $$ {\dot{V}}_x$$와 $$ {\dot{V}}_y$$는 차량의 종방향 및 횡방향 가속도를 의미한다. $$ \dot{\beta }$$는 차량의 측면 슬립각의 변화율, F_yf 및 F_yr은 전방 후방 타이어의 횡방향 힘을 의미한다. 전방 및 후방 타이어의 횡방향 타이어 힘은 아래 식(4)와 식(5)로 표현된다.

$\[ F_{yf}=2C_f\left(\delta -{\theta }_{vf}\right) \]$

(4)

$\[ F_{yr}=2C_r\left(-{\theta }_{vr}\right) \]$

(5)

여기서 θ_vf 및 θ_vr은 전방 및 후방 타이어의 차체 측면 Slip Angle이며, δ는 차량의 입력 조향이다. θ_vf 및 θ_vr은 다음 식(6)과 식(7)과 같이 나타낼 수 있다.

$\[ {\theta }_{vf}=\frac{\beta +L_f\gamma }{V_x} \]$

(6)

$\[ {\theta }_{vr}=\frac{\beta -L_r\gamma }{V_x} \]$

(7)

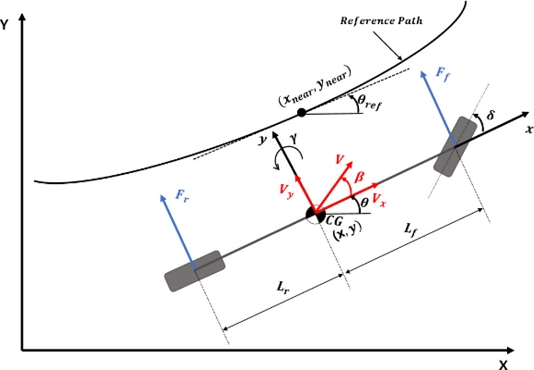
식(4)부터 식(7)을 식(1)과 식(2)에 대입하면 횡방향 모델의 경로 추종에 대한 상태 공간 모델을 생성할 수 있다. 자율주행차량이 실시간으로 경로 추종을 진행할 때, 참조 경로와 차량의 위치에 대한 방향 오차 및 횡방향 거리 오차가 발생하게 된다[17]. 본 논문에서 제안하는 경로 추종 알고리즘에서는 위 두 가지에 대한 오차를 최소한으로 줄여 차량이 참조 경로를 실시간으로 안전하게 주행할 수 있도록 한다. 방향 오차 및 횡방향 거리 오차는 차량의 무게 중심과 참조 경로 사이의 거리 및 방향 오차로 정의한다. 아래 Fig. 2는 경로 추종의 Error Model을 나타내며, 식(8)과 식(9)를 통해 방향 오차 및 횡방향 거리 오차를 나타냈다[18].

$\[ e_0=\sqrt{{\left(x-x_{near}\right)}^2+{\left(y-y_{near}\right)}^2} \]$

(8)

$\[ e_2=\left(\theta -{\theta }_{ref}\right) \]$

(9)

Fig. 2

Path tracking error model

식(8)과 식(9)를 토대로 Error State에 대한 상태벡터를 식(10)을 통해 나타냈다.

$\[ e=\left(e_0,e_1,e_2,e_3\right) \]$

(10)

여기서 e₀는 참조 경로와 차량 무게 중심 사이의 거리이며, e₁는 측면 거리 오차의 변화량, e₂는 차량의 방향과 참조 경로의 탄젠트 기울기 오차이며, e₃는 방향 오차의 변화량이다. 또한, θ_ref는 차량과 가장 가까운 참조 경로의 탄젠트 기울기를 의미하며, (x_near, y_near)는 차량과 가장 가까운 Waypoint 좌표를 나타낸다. 방향 오차 및 횡방향 거리 오차에 대한 차량의 측면 상태 공간 모델은 식(11)과 같다.

$\[ \begin{array}{c}\frac{d}{dt}\left[\begin{array}{c}{e}_0\\ e_1\\ e_2\\ e_3\end{array}\right]=\\ \left(\begin{array}{cccc}0& 1& 0& 0\\ 0& \frac{2C_f+2C_r}{m{V}_x}& \frac{2C_f+2C_r}{m}& \frac{-2C_f{L}_f+2C_r{L}_r}{m{V}_x}.\\ 0& 0& 0& 0\\ 0& -\frac{2C_f{L}_f-2C_r{L}_r}{I_z{V}_x}& \frac{2C_f{L}_f-2C_r{L}_r}{I_z}& \frac{2C_f{L}_f^2+2C_r{L}_r^2}{I_z{V}_x}.\end{array}\right)\left(\begin{array}{c}{e}_0\\ e_1\\ e_2\\ e_3\end{array}\right)+\\ \left(\begin{array}{c}0\\ \frac{2C_f}{m}\\ 0\\ \frac{2C_F{L}_f}{I_z}\end{array}\right)\delta +\left(\begin{array}{c}0\\ -\frac{2C_f{L}_f-2C_r{L}_r}{m{V}_x}-V_x\\ 0\\ -\frac{2C_f{L}_f^2+2C_r{L}_r^2}{I_z{V}_x}\end{array}\right){\dot{\gamma }}_{def }\\ \end{array} \]$

(11)

식(11)의 $$ {\dot{\gamma }}_{def }$$는 곡률 반경에 따라 결정되는 Yaw-rate이다.

2.2 Model Validation

본 논문에서 제안하는 알고리즘 검증을 진행 전에 CARLA Simulator의 차량 모델과 제어 알고리즘의 동역학 모델에 대한 검증을 진행하였다. 검증 방법으로 상태 공간 모델을 만들어 동일한 조향을 입력하여 두 모델의 β과 γ를 비교하였다.

$\[ \left[\begin{array}{c}\dot{\beta }\\ \dot{\gamma }\end{array}\right]=\left(\begin{array}{cc}-\frac{2C_f+2C_r}{m{V}_X}& -1+\frac{-2C_f{L}_f+2C_r{L}_r}{m{V}_x}\\ \frac{-2C_f{L}_f+2C_r{L}_r}{I_z}& -\frac{2C{L}_f{L}_f^2+2C_r{L}_r^2}{I_z{V}_x}\end{array}\right)\left(\genfrac{}{}{0pt}{}{\beta }{\gamma }\right)+\left(\genfrac{}{}{0pt}{}{\frac{2C_f}{m{V}_x}}{\frac{2C_f{L}_f}{I_z}}\right)\text{δ} \]$

(12)

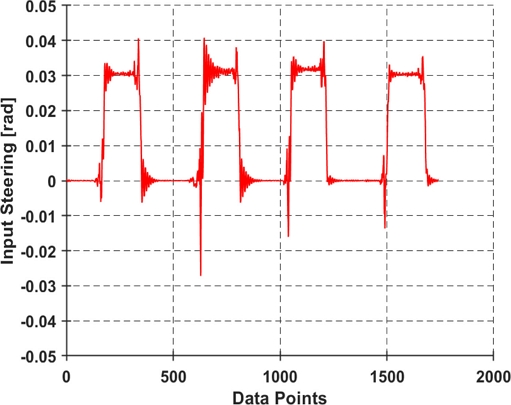
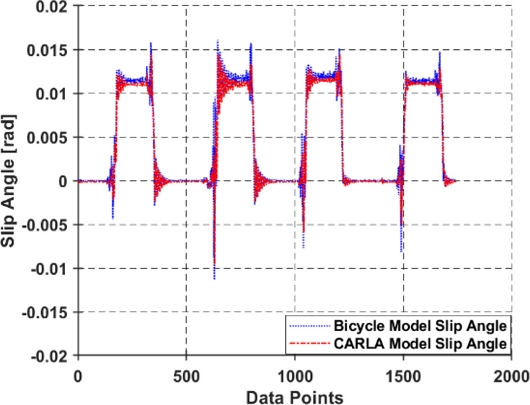
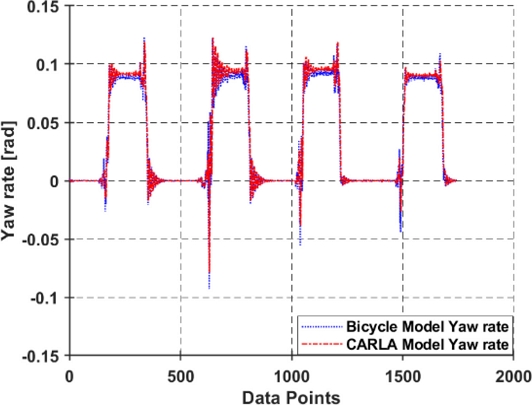
CARLA Simulator의 차량 모델의 경우, β과 γ은 차량에 장착된 GPS와 IMU 센서를 통해 측정하였으며, 아래 Figs. 3-5를 통해 나타냈다. Table 1은 CARLA Simulator 차량의 파라미터를 나타냈다.

Fig. 3

Input steering angle

Fig. 4

Compare side slip angle for validation

Fig. 5

Compare yaw rate for validation

Table 1

Main vehicle parameters

Figs. 3-5는 각각 CARLA Simulator의 차량 모델과 제어 알고리즘의 동역학 모델을 비교하기 위한 차량의 입력 조향 δ 및 β과 γ을 나타낸다. Figs. 4, 5와 같이 CARLA Simulator 차량 모델과 제어 알고리즘의 동역학 모델을 비교하였을 때, 동일한 조향에 대해 β과 γ이 근사한 값이 출력이 되는 것을 확인할 수 있다.

3. Lateral Control System

3.2 Curvature-based Feed-forward Control

3.2.1 Preview Distance

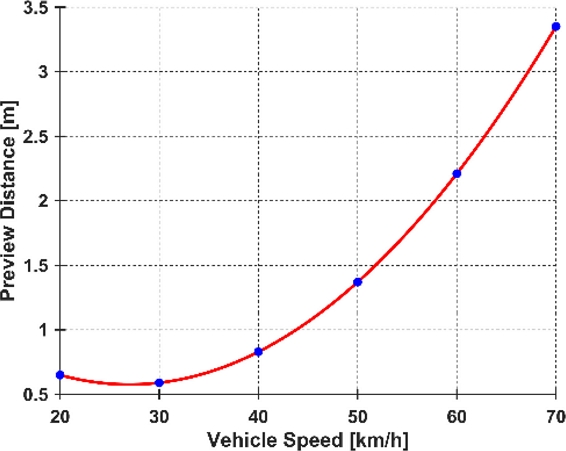
자율주행 차량이 직진 구간을 지나 급격한 커브 구간을 진입하기 전에 전방 도로 상황을 알고 커브 구간의 곡률에 대한 적절한 조향을 차량에 인가하는 것이 중요하다. 차량 속력이 저속일 때 Preview Distance를 고려하지 않고 주행을 해도 크게 문제가 되지 않지만, 고속에서 Preview Distance를 전혀 고려하지 않고 선회할 경우, 급격한 오차의 증가로 순간적으로 큰 조향이 차량에 인가되기 때문에 위험한 상황이 발생할 수 있다. 본 논문에서는 실제 운전자의 차량 제어의 원리를 적용하기 위해 차량 속력에 대한 Preview Distance를 사용하였다. Fig. 6은 식(20)의 결과 그래프이다. 즉, 차량의 속력 V_x에 대해 Preview Distance의 값을 알 수 있다. 이는 주행 실험을 통해 방향 오차 및 횡방향 거리 오차가 최솟값으로 출력되는 Preview Distance의 값을 도출하여 차량 속력에 대한 2차 방정식으로 유도하였다.

$\[ \text{Preview Distance }\approx 0.0015V_x^2-0.081V_x+1.67 \]$

(20)

Fig. 6

Preview distance for vehicle speed

본 논문에서 사용되는 Preview Distance의 개념이 Pure Pursuit 알고리즘의 Look-ahead Distance와 같이 일정거리의 전방을 주시하는 개념은 동일하지만 세부적으로는 다른 내용이 존재한다. Pure Pursuit의 Look-ahead Distance 개념의 경우 오로지 목표점을 추적하는 데 사용되지만, 본 논문에서 언급하는 Preview Distance의 경우에는 차량의 현재 위치와 미래의 도로 정보를 먼저 파악하여 경로의 변화에 과도하게 반응하지 않고 미리 대응할 수 있도록 Curvature-based Feed-forward 방식을 설계하였다. 이에 대한 내용은 아래의 Fig. 7에 나타냈다.

Fig. 7

Comparison of preview distance and look-ahead distance

3.2.2 Curvature Calculation

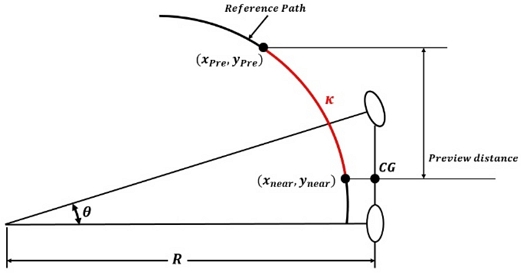
곡률은 직선 혹은 곡면이 휘어진 정도를 의미한다. 본 논문에서는 곡률을 구하기 위해 차량과 가장 가까운 Waypoint와 Preview Distance의 길이에 존재하는 Waypoint를 사용하여 곡률 κ을 구하였다. Fig. 8는 경로상의 곡률을 나타낸다.

Fig. 8

Curvature on reference path

여기서 곡률 κ는 아래 식(21)과 같이 구할 수 있다.

$\[ \kappa =f\left({\left(x_{pre}\right)}^{\text{'}},{\left(y_{pre}\right)}^{\text{'}}\right)=\frac{\left|{\left(y_{pre}\right)}^{\text{'}\text{'}}{\left(x_{pre}\right)}^{\text{'}}-{\left(x_{pre}\right)}^{\text{'}\text{'}}{\left(y_{pre}\right)}^{\text{'}\text{'}}\right|}{{\left\{{\left(x_{pre}\right)}^{\text{'}2}+{\left(y_{pre}\right)}^{\text{'}2}\right\}}^{1.5}} \]$

(21)

곡률 κ가 0에 가까운 값을 나타내는 경우는 휘어진 정도가 거의 없는, 즉 직선 구간임을 의미한다. 또한 x_pre'와 y_pre', x_pre''와 y_pre''는 참조 경로의 Waypoint (x, y)를 최소 제곱법을 이용하여 아래 식(22)와 같이 4차 다항식의 형태로 나타낼 수 있다.

$\[ \begin{array}{c}{x}_{pre }=ax{\sigma }^4+bx{\sigma }^3+cx{\sigma }^2+dx\sigma +ex\hfill \\ y_{pre }=ay{\sigma }^4+by{\sigma }^3+cy{\sigma }^2+dy\sigma +ey\hfill \\ {x_{pre}}^{\text{'}}=4ax{\sigma }^3+3bx{\sigma }^2+2cx\sigma +dx\hfill \\ {y_{pre}}^{\text{'}}=4ay{\sigma }^3+3by{\sigma }^2+2cy\sigma +dy\hfill \\ {x_{pre}}^{\text{'}}=12ax{\sigma }^2+6bx\sigma +2cx\hfill \\ {y_{pre}}^{\text{'}}=12ay{\sigma }^2+6by\sigma +2cy\hfill \end{array} \]$

(22)

여기서 ax, bx, cx, dx, ex와 ay, by, cy, dy, ey는 Waypoint (x, y)에 대한 다항식의 계수를 의미하며, σ는 0에서 1까지의 값을 가질 수 있는 매개변수의 형태로 본 논문에서는 차량의 실시간 위치와 참조 경로에 대한 Preview Distance를 사용하여 구하였다. 식(21)의 계산은 식(22)을 미분하여 구할 수 있다. 이러한 과정은 매개변수 σ의 값에 의해 Waypoint (x, y)가 계산되며, 이는 참조 경로를 반복적으로 계산하여 연속적이고 부드러운 경로를 형성할 수 있다.

3.2.3 Ackermann Steering

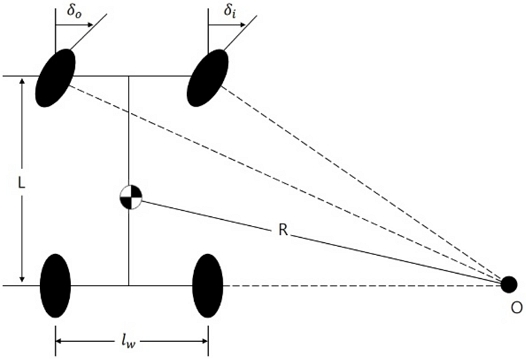
Bicycle Model에서는 왼쪽 및 오른쪽 바퀴를 하나의 바퀴로 가정한다[21]. 이는 실제로 왼쪽 및 오른쪽 바퀴의 조향이 같다는 가정이지만, 정확하게 일치하지 않는다. 이는 왼쪽 및 오른쪽 바퀴가 이동하는 경로의 반경이 다르기 때문이다[22]. 또한 차량의 속력이 저속일 경우에는 타이어 횡력을 발생시킬 필요가 없으며, 아래 Fig. 9과 같이 선회해야 한다. Fig. 11은 전륜 차량의 이상적인 선회를 나타낸 차량의 기하학적 구조를 나타낸다.

Fig. 9

Geometry of a turning vehicle

Fig. 9에서 δ_o와 δ_i는 각각 바깥쪽 및 안쪽 바퀴 조향, l_w는 차량의 너비, L은 차량의 Wheelbase를 나타내며, R은 무게 중심점과 선회 중심각의 거리, 즉 곡률 반경을 의미한다. 여기서 곡률 반경 R은 곡률 κ의 역수이다. 또한 Wheelbase L은 곡률 반경 R보다 작아야 한다. 위와 같은 조건을 만족하는 기하학적 차량의 각 바퀴에 대한 서로 다른 조향은 아래와 같이 표현할 수 있다.

$\[ {\delta }_o=\frac{L}{\left(R+\frac{l_w}{2}\right)} \]$

(23)

$\[ {\delta }_i=\frac{L}{\left(R-\frac{l_w}{2}\right)} \]$

(24)

무게 중심점의 조향을 δ_ff라고 표현하고, δ_ff이 바깥쪽 및 안쪽 조향의 평균이라 하면, δ_ff는 식(25)와 같이 나타낼 수 있다[23].

$\[ {\delta }_{ff}=\frac{{\delta }_o+{\delta }_i}{2}=\frac{LR}{R^2-\frac{w^2}{4}}\fallingdotseq \frac{L}{R} \]$

(25)

결론적으로 자율주행 차량의 입력 조향 δ는 식(26)과 같이 표현할 수 있다.

$\[ \delta ={\delta }_{ff}+{\delta }_{fb} \]$

(26)

4. Simulation

4.1 CARLA Simulator

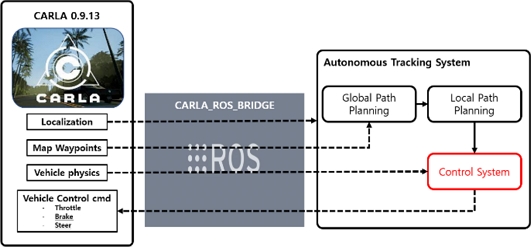
ROS 환경의 Ubuntu 20.04 OS에서 CARLA Simulator 및 CARLA ROS Bridge 0.9.13 버전을 사용하여 논문에서 제안하는 경로 추종 알고리즘 개발 및 검증을 진행하였다. CARLA ROS Bridge를 사용하여 CARLA Simulator와 ROS 간의 양방향 통신을 가능하게 하였다.

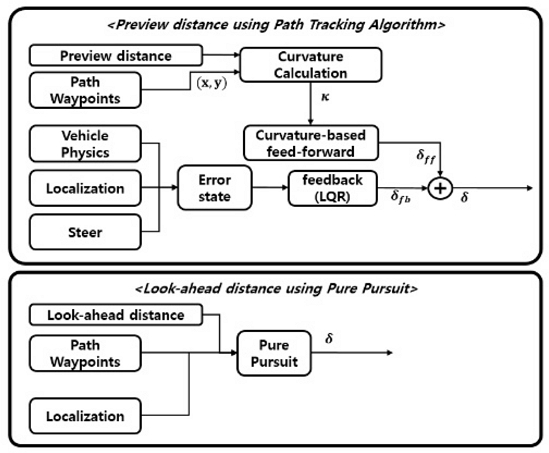
Fig. 10은 연구의 전체 시스템의 개략도를 나타낸다. CARLA ROS Bridge를 통해 CARLA Simulator에서 제공하는 차량의 파라미터, 맵 Waypoint 및 각종 센서 데이터를 경로 추종 알고리즘에 전송하며, 전송된 데이터를 바탕으로 차량을 제어하게 된다.

Fig. 10

Overall system architecture

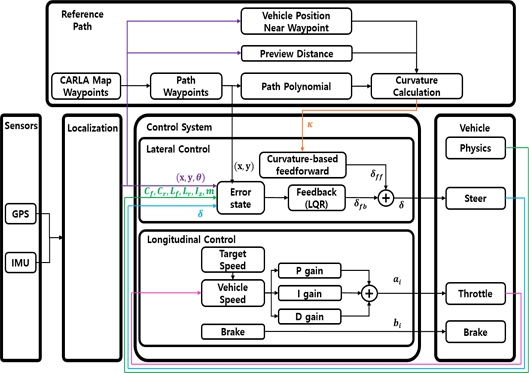
4.2 Control System Architecture

Fig. 11은 논문에서 제안하는 경로 추종 알고리즘의 개략도를 나타낸다. CARLA Simulator 맵의 Waypoint와 차량의 위치 정보를 이용하여 참조 경로에서의 곡률의 크기를 구할 수 있다. 또한, 가중치 행렬 Q와 상수 R 및 Preview Distance의 값을 도출한 뒤 Feedback (LQR) Control과 Curvature-based Feed-forward Control의 합산 조향을 차량에 입력하였다.

Fig. 11

Control system architecture of the proposed algorithm

4.4 첫 번째 시뮬레이션

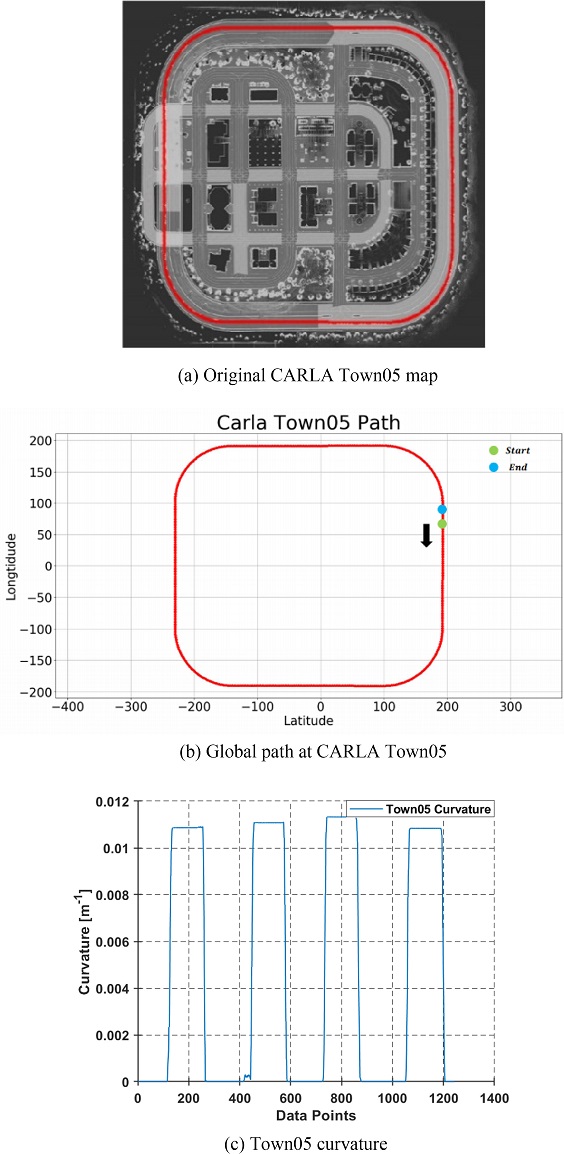
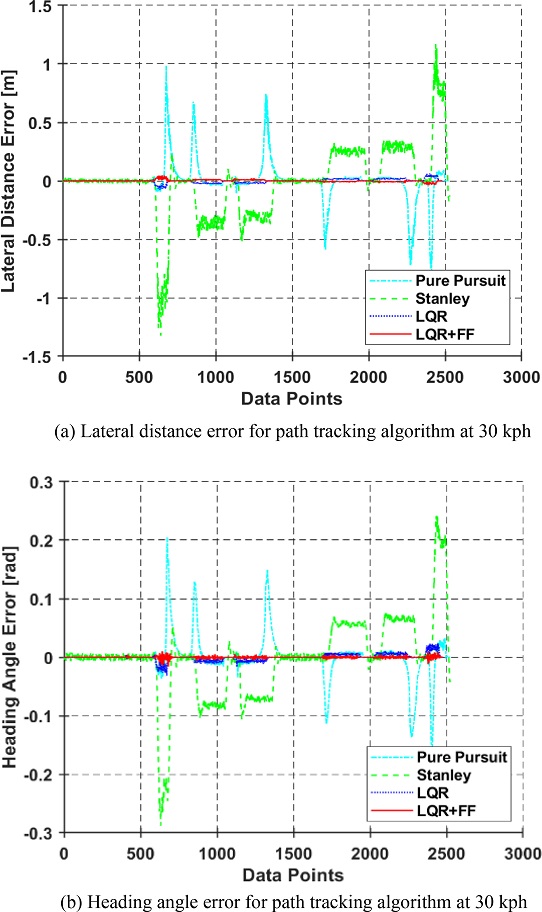
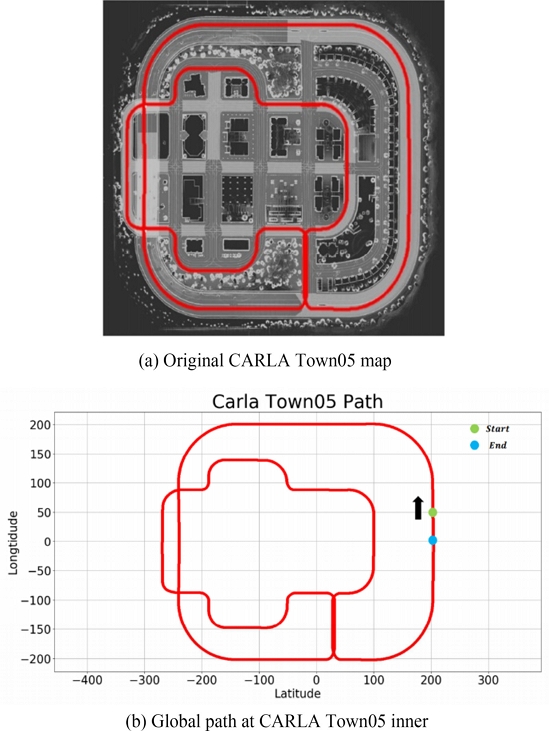
첫 번째 시뮬레이션에서는 Town05 맵의 외각을 따라 주행하는 실험을 진행하였으며, Fig. 12는 첫 번째 시뮬레이션에서 사용된 참조 경로를 보여준다. 이 참조 경로는 외곽 지역을 제외한 모든 Waypoint를 필터링하여 제거한 결과이다. 해당 참조 경로에서의 실험 결과는 Figs. 13과 14 및 Tables 2와 3에서 확인할 수 있다.

Fig. 12

Creation of a driving path using waypoints in CARLA Town05

Fig. 13

Heading & lateral distance error with steering at a vehicle speed of 30 kph in Town05

Fig. 14

Heading & lateral distance error with steering at a vehicle speed of 60 kph in Town05

Table 2

Heading & lateral distance error RMS at vehicle speed of 30 kph in Town05

Table 3

Heading & lateral distance error RMS at vehicle speed of 60 kph in Town05

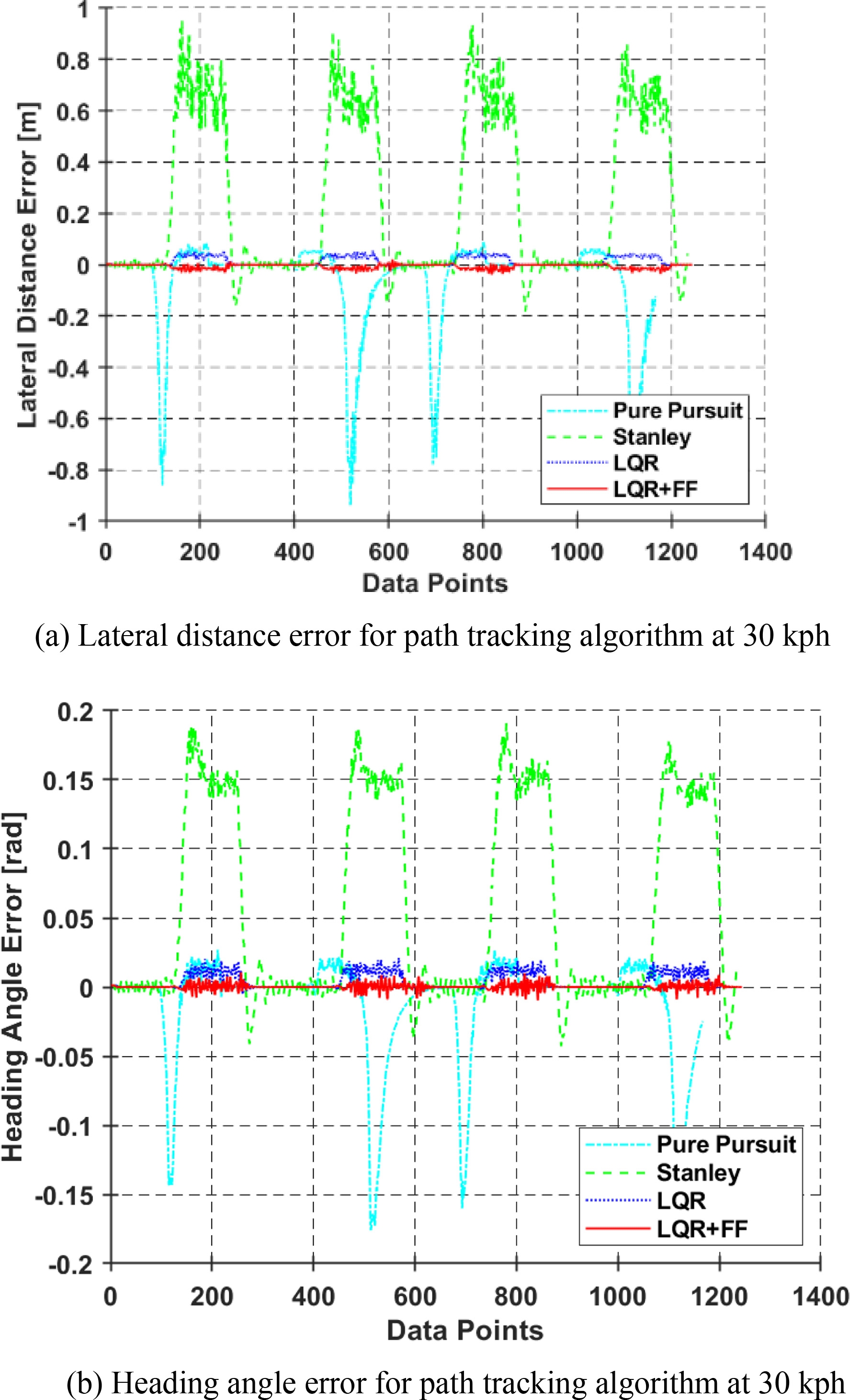
Fig. 13은 Town05 맵에서 차량 속력 30 kph에 대한 방향 오차 및 횡방향 거리 오차를 보여준다. Figs. 13(a)와 13(b)를 통해 다른 추종 알고리즘에 비해 논문에서 제안하는 알고리즘의 추종 성능이 뛰어난 것을 확인할 수 있다. 이는 차량이 참조 경로를 추종하는 데 있어 Feedback Control과 Feed-forward Control의 결합이 경로 추종에 더욱 효과적이라 할 수 있다. Fig. 13의 y축은 참조 경로를 기준으로 한 차량의 좌측 및 우측 거리와 방향오차를 나타내며, 차량이 선회하는 동안 오차가 증가하는 것을 확인할 수 있다. Fig. 13의 내용에서 PP와 Stanley Method는 선회 구간에서 LQR및 LQR+FF에 비해 추종 성능이 많이 떨어지는 것을 확인할 수 있다. Figs. 13(a)과 13(b)에 대한 RMS는 Table 2를 통해 나타냈다.

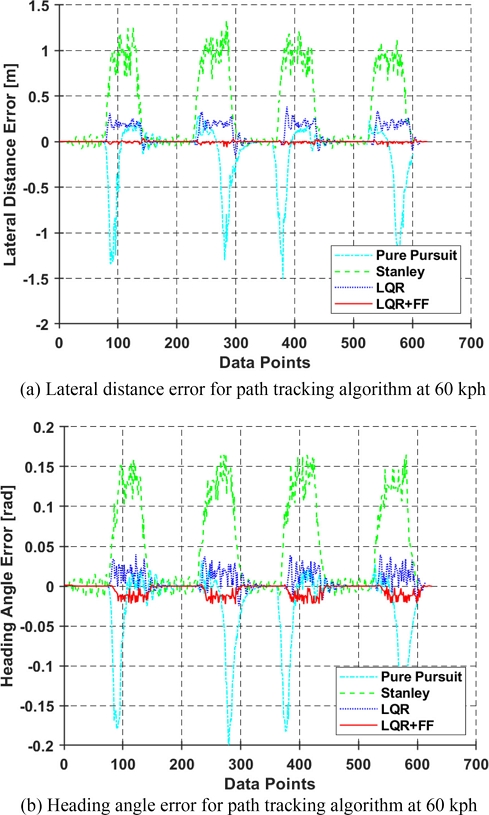
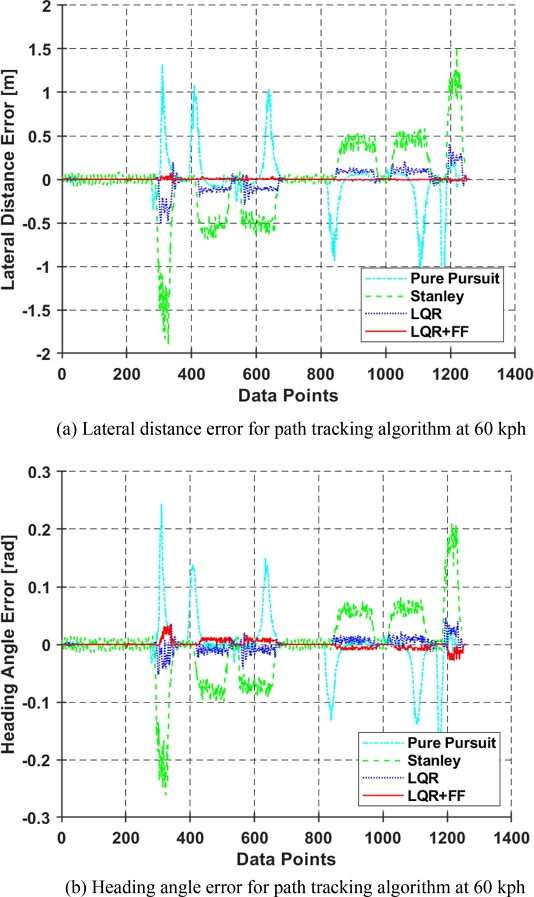
Fig. 14는 Town05 맵에서 차량이 60 kph의 속력으로 주행할 때의 방향 오차 및 횡방향 거리 오차를 보여준다. Fig. 13과 마찬가지로, 논문에서 제안하는 경로 추종 알고리즘이 가장 성능이 뛰어난 것을 확인할 수 있다. Table 3을 통해 횡방향 거리 오차값이 Table 2에 비해 크게 상승한 그 이유는 선회 구간에서 차량의 속력을 줄이지 않고 정속 주행을 진행한 결과이며, 선회 구간 진입 전 차량의 속력을 줄일 경우 오차가 크게 감소할 것으로 예상된다.

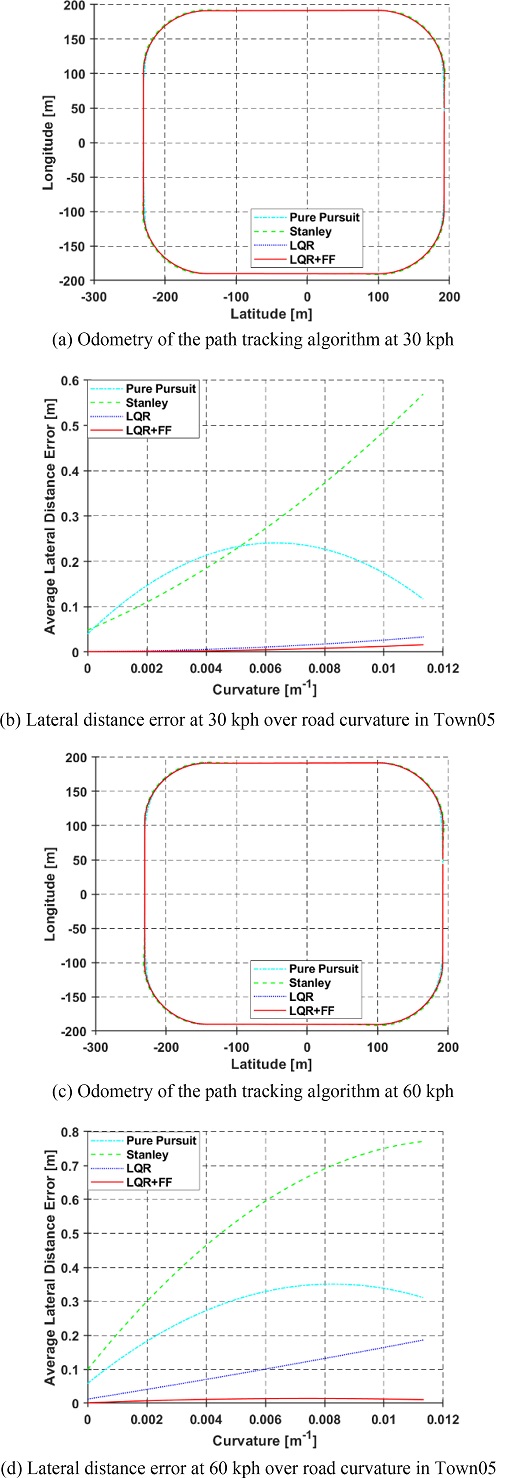
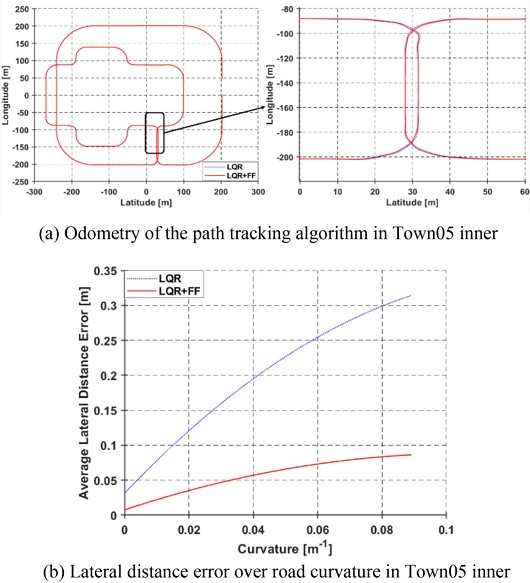
Figs. 15(a)와 15(c)는 Town05 맵 에서 30 kph와 60 kph의 경로 추정의 Odometry값을 보여준다. 직선 구간에서는 크게 차이가 없지만, 선회 구간에서 조금씩 차이가 발생한다. Figs. 15(b)와 15(d)는 각 차량 속력에서 Town05 맵 곡률 크기에 따른 횡방향 거리 오차를 나타낸다. 30 kph 속력에서 PP방식을 사용한 차량은 선회 초기에 참조 경로에서 벗어났지만, 점차 오차가 줄어들었다. 반면 Stanley 방식을 사용할 때는 차량이 선회하는 동안 참조 경로를 크게 이탈하는 것을 확인할 수 있었다. LQR과 LQR+FF의 경우에는 30 kph에서는 두 알고리즘 모두 크게 차이가 없지만, 60 kph에서는 차량이 선회하는 동안 LQR 알고리즘의 오차가 크게 증가하는 것을 확인할 수 있다. 이를 통해 논문에서 제안된 추종 알고리즘이 Town05 맵의 해당 곡률에서 가장 우수한 성능을 보임을 확인할 수 있다.

Fig. 15

Odometry of the path tracking algorithm and heading & lateral distance error at 30 & 60 kph over curvature in Town05

4.5 두 번째 시뮬레이션

CARLA Town05 맵에서 경로 추종 알고리즘에 대한 추가 검증을 위해 CARLA Town04 맵에서 두 번째 시뮬레이션을 진행하였다. Fig. 16은 추가 검증 실험을 진행하기 위해 Fig. 12과 같이 해당 맵의 참조 경로를 생성한 결과이다. 차량의 속력에 대한 가중치 행렬 Q와 R 및 Preview Distance는 CARLA Town05 맵에서의 실험과 동일하게 적용하였으며, 동일하게 타 추종 알고리즘인 PP와 Stanley Method, LQR을 사용한 실험도 추가하였다. 결과는 아래 Figs. 17과 18 및 Tables 4와 5에서 확인할 수 있다.

Fig. 16

Creation of a driving path using waypoints in CARLA Town04

Fig. 17

Heading & lateral distance error with steering at a vehicle speed of 30 kph in Town04

Fig. 18

Heading & lateral distance error with steering at a vehicle speed of 60 kph in Town04

Table 4

Lateral distance error and heading angle error RMS at vehicle speed of 30 kph in Town04

Table 5

Lateral distance error and heading angle error RMS at vehicle speed of 60 kph in Town04

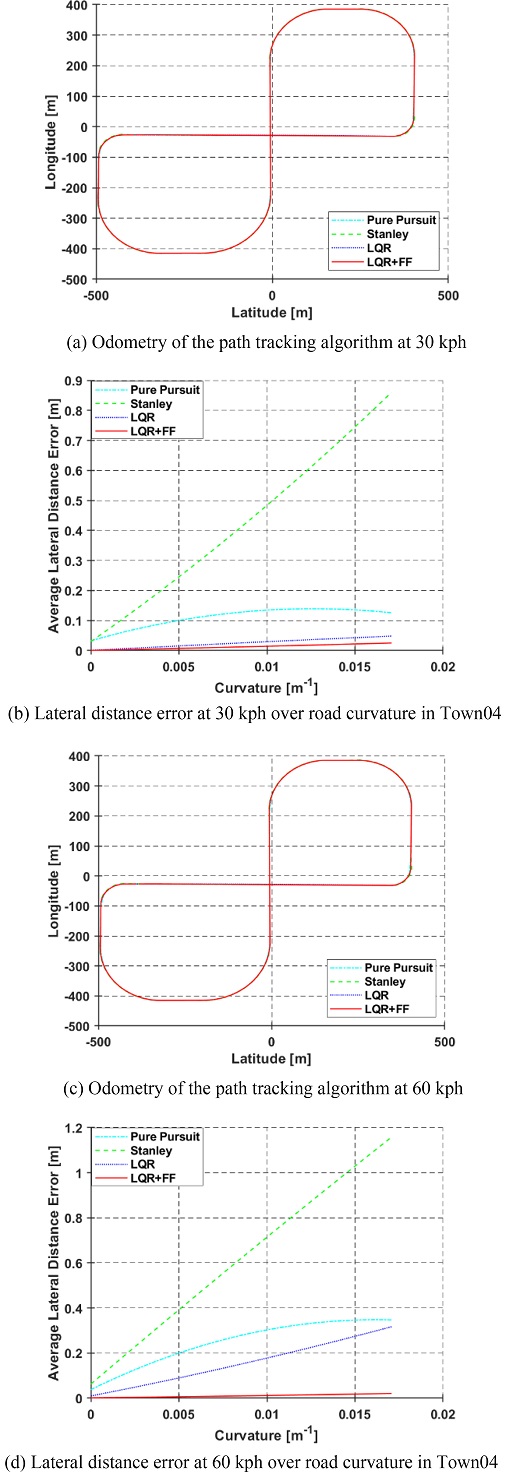
Fig. 17는 CARLA Town04 맵에서 차량의 속력이 30 kph일 때, 방향 오차 및 횡방향 거리 오차를 나타낸다. Town04 맵은 Town05 맵과 다르게 도로 곡률의 크기가 다양하며, 좌회전과 우회전이 모두 포함되어 있다. 이 맵에서는 총 6개의 곡률이 존재하며, 전방 3개는 좌회전, 후방 3개는 우회전 경로이다. 실험결과, Town05에서와 마찬가지로 본 논문에서 제안하는 경로 추종 알고리즘의 성능이 우수한 것을 확인할 수 있다. Fig. 17에 대한 RMS는 Table 4를 통해 나타냈다.

Figs. 18은 17과 같이 CARLA Town04 맵에서 차량의 속력 60 kph일 때, 방향 오차 및 횡방향 거리 오차를 나타낸다. Fig. 14와 같이 차량이 고속 주행 중 선회 구간에서 차량의 속력을 줄이지 않고 주행을 한다면 횡방향 거리 오차가 크게 증가한다. 방향 오차의 경우에는 선회 구간을 진입하기 전과 후에 방향이 크게 틀어지는 것을 확인할 수 있다. Fig. 18에 대한 RMS는 Table 5를 통해 나타냈다.

Figs. 19(a)와 19(c)는 Town04 맵 에서 30와 60 kph의 경로 추정의 Odometry 값을 나타낸다. Fig. 15와 같이 직선 구간에서는 크게 차이가 없지만, 선회 구간에서 조금씩 차이가 발생하는 것을 확인할 수 있다. Figs. 19(b)와 19(d)는 Town04 맵의 곡률의 크기에 따른 횡방향 거리 오차를 나타낸다. Town05와 마찬가지로 Town04에서도 추종 알고리즘의 성능이 비슷한 결과를 나타낸다.

Fig. 19

Odometry of the path tracking algorithm and heading & lateral distance error at 30 & 60 kph over Curvature in Town04

4.6 세 번째 시뮬레이션

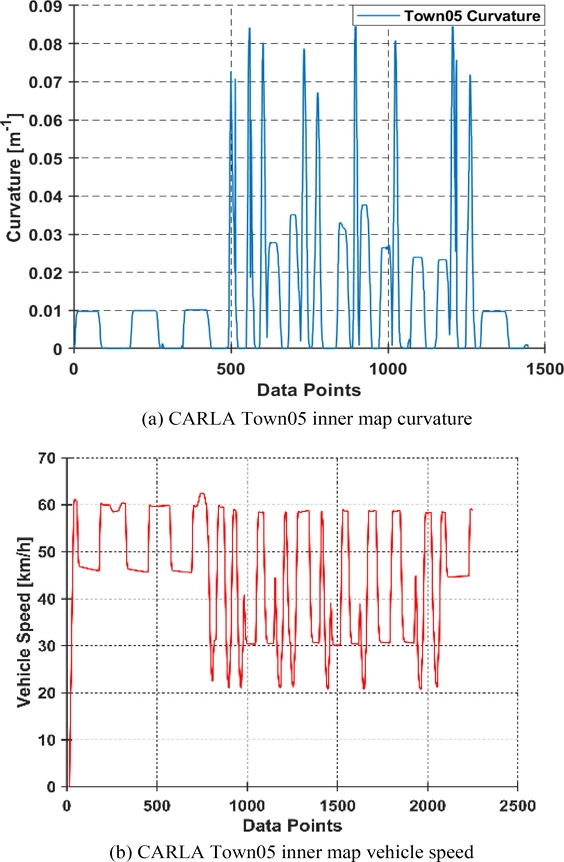
Fig. 20은 다양한 곡률의 크기에 따른 차량 속력의 제한을 걸어 경로 추종 검증을 진행하였다. 4.4장과 4.5장에서는 동일한 속력, 크게 다르지 않은 곡률의 크기에서 경로 추종을 검증하는 과정을 진행하였으나, 실제 도로에서는 곡률의 크기가 다양하게 분포되어 있기 때문에 세 번째 시뮬레이션으로 CARLA Town05 맵의 내부 공간을 주행할 수 있는 참조 경로를 생성하였다. Fig. 20에 대한 곡률의 크기와 그에 따른 차량의 속력 변화 및 차량의 입력 조향은 아래 Fig. 21을 통해 나타냈다.

Fig. 20

Creation of a driving path using waypoints in CARLA Town05-inner map

Fig. 21

CARLA Town05-inner map curvature and vehicle speed

Figs. 21(a)와 21(b)의 내용을 통해 아래 Table 6을 작성하였다. Table 6은 곡률의 크기에 따라 차량의 속력을 부여하는 것을 의미하며, 세 번째 시뮬레이션의 실험 결과는 아래 Fig. 22를 통해 나타냈다.

Table 6

Vehicle speed according to value of curvature

Fig. 22

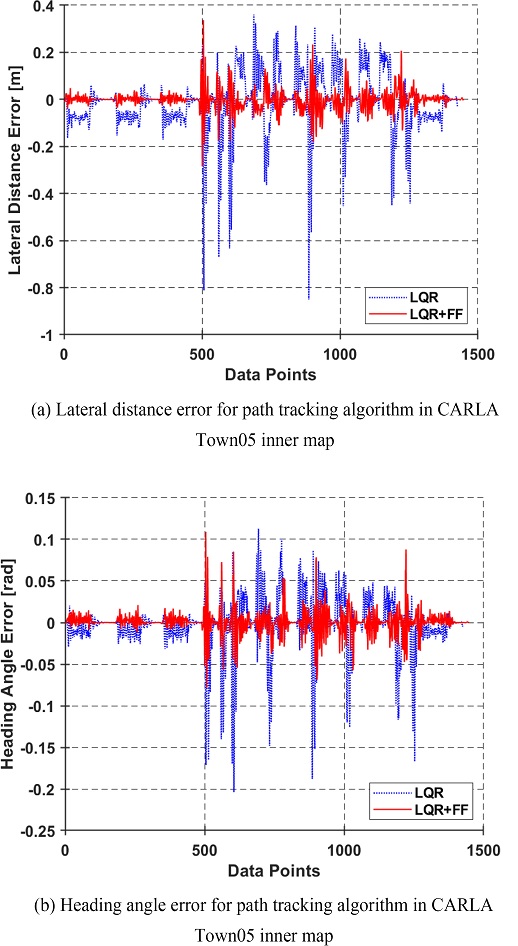
Heading & lateral distance error of δfb + δff in CARLA Town05 inner map for curvature and speed of vehicle

Figs. 22는 20의 참조 경로에서 경로 추종 실험을 진행하였을 때, 방향 오차 및 횡방향 거리 오차에 대한 결과를 나타낸다. 차량이 해당 참조 경로를 주행하는 동안 Preview Distance를 사용하여 경로의 곡률을 감지하였을 때 해당 곡률의 최댓값을 기반으로 차량의 속력을 제한하였다. 또한 첫 번째와 두 번째 시뮬레이션과 동일하게 논문에서 제안하는 경로 추종 알고리즘의 성능이 뛰어난 것을 확인할 수 있다. Fig. 22를 통해 곡률이 가장 큰 부분을 주행할 때 방향 오차 및 횡방향 거리 오차의 값이 크게 증가하는 것을 확인할 수 있다. 초기 직선과 가까운 크기를 가진 곡률에서는 Table 6과 같이 60 kph의 속력으로 주행을 하다가 곡률의 크기가 바뀌면서 속도 제한으로 인해 차량의 속력이 변하게 된다. 이로 인해 가중치 행렬 Q와 상수 R 및 Preview Distance의 값들도 해당 속도의 최적값으로 변하게 되면서 경로 추종에 영향을 미치는 것이라 판단된다. Fig. 22에 대한 RMS는 Table 7을 통해 나타냈다.

Table 7

Lateral distance error and heading angle error RMS at vehicle speed of 20-60 kph in Town05

Fig. 23(a)는 Town05 맵의 내부 경로에서의 경로 추정의 Odometry 값을 나타낸다. 첫 번째와 두 번째 시뮬레이션과 같이 직선 구간에서는 크게 차이가 없지만, 선회 구간에서 조금씩 차이가 발생하는 것을 확인할 수 있다. Fig. 23(b)는 곡률 크기에 대한 횡방향 거리 오차를 나타낸다.

Fig. 23

Odometry of the path tracking algorithm and heading & lateral distance error over curvature in Town05 inner

5. Conclusion

본 논문에서는 CARLA Simulator를 활용하여 자율주행 차량의 운전 환경을 모사하고, 운행 안정성 향상을 위한 경로 추종 알고리즘을 개발 및 검증하였다. 차량의 입력 조향으로는 Pure Pursuit (PP), Stanley Method, Feedback (LQR) Control 및 Feedback (LQR) Control+Curvature-based Feed-forward (FF)를 사용하였다. 이러한 추종 알고리즘의 성능은 세 가지 시뮬레이션을 통해 비교되었으며, 그 결과 각 알고리즘의 성능 차이를 아래와 같이 확인할 수 있었다.

첫 번째 시뮬레이션에서는 곡률의 크기가 비슷한 도심 환경에서 30와 60 kph 속력으로 비교 실험을 진행하였다. 논문에서 제안하는 추종 알고리즘의 경우 30 kph에서 PP보다 방향 오차는 97.06%, Stanley보다 98.53%의 성능 향상을 보였으며, Feedback(LQR)보다 80%의 상대적 성능 향상을 보였다. 횡방향 거리 오차 역시 각각 95, 97.29, 50%가 향상된 것을 확인하였다. 비슷하게 60 kph에서 방향 오차와 횡방향 거리 오차에서 각각 90.2, 93.83, 50% 및 84.62, 89.47, 33%의 향상을 확인하였다.

두 번째 시뮬레이션에서는 첫 번째 시뮬레이션과 다르게 곡률의 크기가 다른 도심 환경에서 진행되었으며, 30 kph와 60 kph의 2공속도에서 비교 실험을 진행하였다. 30 kph에서는 PP보다 88.24%, Stanley보다 94.2%, LQR 보다는 20%의 성능 향상을 보였으며, 횡방향 거리 오차 역시 각각 91.33, 95.79, 18.75%의 향상을 보였다. 60 kph에서의 방향 오차 및 횡방향 거리 오차는 각각 85.71, 90.16, 40% 및 96.7, 97.92, 91.26%의 향상을 확인하였다.

세 번째 시뮬레이션에서는 다양한 곡률 크기와 차량 속력을 조절하며 진행되었다. 세 번째 시뮬레이션에서는 PP와 Stanley를 제외한 LQR과 비교 실험을 진행하였다. 이 실험에서도 논문에서 제안하는 추종 알고리즘이 방향 오차는 60.61%, 횡방향 거리 오차의 경우 68.7%의 성능 향상을 확인하였다.

세 가지 시뮬레이션을 통해, 본 논문에서 제안하는 추종 알고리즘이 저속과 고속 모두에서 다른 알고리즘보다 우수한 성능을 보임을 확인하였다. 향후에는 자율주행 차량의 센서나 액추에이터 등 핵심 부품의 문제가 발생할 경우에도 안정적으로 고속 주행이 가능한 강건한 제어 알고리즘 개발에 대한 연구를 진행할 계획이다.

Acknowledgments

본 결과물은 농림축산식품부의 재원으로 농림식품기술기획평가원(노지분야 스마트 농업기술 단기 고도화 사업)의 지원을 받아 연구되었음(No. 322030-3).

REFERENCES

• Andersen, H., Chong, Z. J., Eng, Y. H., Pendleton, S., Ang, M. H., (2016), Geometric path tracking algorithm for autonomous driving in pedestrian environment, 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 1669-1674. [https://doi.org/10.1109/AIM.2016.7577010]
• Hossain, T., Habibullah, H., Islam, R., (2022), Steering and speed control system design for autonomous vehicles by developing an optimal hybrid controller to track reference trajectory, Machines, 10(6), 420. [https://doi.org/10.3390/machines10060420]
• Raffo, G. V., Gomes, G. K., Normey-Rico, J. E., Kelber, C. R., Becker, L. B., (2009), A predictive controller for autonomous vehicle path tracking, IEEE Transactions on Intelligent Transportation System, 10(1), 92-102. [https://doi.org/10.1109/TITS.2008.2011697]
• Gámez Serna, C., Ruichek, Y., (2017), Dynamic speed adaptation for path tracking based on curvature information and speed limits, Sensor, 17(6), 1383. [https://doi.org/10.3390/s17061383]
• Ang, K. H., Chong, G., Li, Y., (2005), PID control system analysis, design, and technology, IEEE Transactions on Control Systems Technology, 13(4), 559-576. [https://doi.org/10.1109/TCST.2005.847331]
• Farag, W., (2020), Complex trajectory tracking using PID control for autonomous driving, International Journal of Intelligent Transportation Systems Research, 18(2), 356-366. [https://doi.org/10.1007/s13177-019-00204-2]
• Cibooglu, M., Karapinar, U., Soylemez, M. T., (2017), Hybrid controller approach for an autonomous ground vehicle path tracking problem, 2017 25th Mediterranean Conference on Control and Automation (MED), 583-588. [https://doi.org/10.1109/MED.2017.7984180]
• Samuel, M., Hussein, M., Mohamad, M. B., (2016), A review of some pure-pursuit based path tracking techniques for control of autonomous vehicle, International Journal of Computer Applications, 135(1), 35-38. [https://doi.org/10.5120/ijca2016908314]
• Campbell, S. F., (2007), Steering control of an autonomous ground vehicle with application to the DARPA urban challenge, M.Sc. Thesis, Massachusetts Institute of Technology.
• Thrun, S., Montemerlo, M., Dahlkamp, H., Stavens, D., Aron, A., Diebel, J., Fong, P., Gale, J., Halpenny, M., Hoffmann, G., Lau, K., Oakley, C., Palatucci, M., Pratt, V., Stang, P., Strohband, S., Dupont, C., Jendrossek, L.-E., Koelen, C., Markey, C., Rummel, C., Niekerk, J. V., Jensen, E., Alessandrini, P., Bradski, G., Davies, B., Ettinger, S., Kaehler, A., Nefian, A., Mahoney, P., (2006), Stanley: The robot that won the DARPA grand challenge, Journal of Field Robotics, 23(9), 611-692. [https://doi.org/10.1002/rob.20147]
• Wu, J., Fu, Q., Liu, Y., Sun, B., (2021), Trajectory following control for autonomous vehicles using the feedforward controller and the improve trajectory following model, International Journal of Innovative Computing, Information and Control, 17(6), 2019-2032.
• Zhou, Z., Rother, C., Chen, J., (2023), Event-triggered model predictive control for autonomous vehicle path tracking: validation using CARLA simulator, IEEE Transactions on Intelligent Vehicles, 3547-3555. [https://doi.org/10.1109/TIV.2023.3266941]
• Stevan, S., Momčilob, K., Markoa, D., Nives, K., (2020), Development of ADAS perception applications in ROS and “Software-In-the-Loop” validation with CARLA simulator, Telfor Journal, 12(1), 40-45. [https://doi.org/10.5937/telfor2001040S]
• Gutierrze, R., Lopez-Guillen, E., Bergasa, L. M., Barea, R., Perez, O., Gomez-Huelamo, C., Arango R., Egido, J. D., Lopez-Fernandez, J., (2020), A waypoint tracking controller for autonomous road vehicles using ROS framework, Sensors, 20(14), 4062. [https://doi.org/10.3390/s20144062]
• CARLA, CARLA Open-source simulator for autonomous driving research. https://Carla.org
• Jo, A., (2022), Robust hierarchical motion planning and control for automated bus, Ph.D. Thesis, Seoul National University.
• Yang, T., Bai, Z., Li, Z., Feng, N., Chen, L., (2021), Intelligent vehicle lateral control method based on feedforward + predictive lqr algorithm, Actuators, 10(9), 228. [https://doi.org/10.3390/act10090228]
• Vivek, A., Sheta, M. A., Gumtapure, V., (2019), A comparative study of Stanley, LQR and MPC controllers for path tracking application (ADAS/AD), 2019 IEEE International Conference on Intelligent Systems and Green Technology (ICISGT).
• Chen, Y., Zheng, Y., (2022), A review of autonomous vehicle path tracking algorithm research, Authorea Preprints. [https://doi.org/10.22541/au.166990184.45015188/v1]
• Li, H., Li, P., Yang, L., Zou, J., Li, Q., (2022), Safety research on stabilization of autonomous vehicle based on improved-LQR control, AIP Advances, 12(1), 1-13. [https://doi.org/10.1063/5.0078950]
• Snider, J. M., (2009), Automatic steering method for autonomous automobile path tracking, Robotics Institute, Carnegie Mellon University, CMU-RITR-09-08.
• Rajesh, R., (2005), Vehicle dynamics and control, Springer Science & Business Media.
• Thomas, D, G., (1992), Fundamentals of vehicle dynamic, Society of Automotive Engineers.