다물체동역학기반 실시간 원격주행 시뮬레이터 개발
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Autonomous robots are commonly operated on rough roads. Thus, it is essential to predict their dynamic characteristics. Even though it is possible to use real hardware to acquire a robot’s dynamic characteristics, this requires a significant amount of time and cost. Therefore, a real-time remote driving simulator must be developed to reduce these risks. Most real-time simulators employ physics engines, which are calculated using simple functional expressions based on particles. However, in this case, there is a limit to reflecting the dynamic characteristics of actual robots. In this study, a multi-body dynamic model of a robot was established. MATLAB Simulink was used to connect the vehicle model with the joystick and calculate user input signals. The PID control system determines the driving torque of the robot to satisfy the calculated signal. Gain value optimization is performed to enable real-time control. This study can be available to analyze the traversability.
Keywords:
Real-time, Simulator, Joystick, Autonomous robot, Multi-body dynamics, PID control키워드:
실시간, 시뮬레이터, 조이스틱, 자율주행로봇, 다물체 동역학, PID 제어1. 서론
최근 무인 주행에 대한 기술이 발전함에 따라 다양한 노면에 대한 주행 기술 연구가 증가하고 있다. 무인 로봇은 일반 도로와 같이 규격화되어 있는 도로를 주행하는 경우도 있지만 주로 사람이 임무를 수행하기 어려운 험지와 같은 환경에서 원격주행이나 자율주행으로 운용된다. 이러한 험지와 같이 험난한 지형에서 로봇을 무인으로 주행시키기 위해서는 로봇의 정확한 동특성 분석이 중요하다. 차량의 동특성은 시험을 통해서도 확보가 가능하지만 실제 하드웨어를 주행시킬 경우 많은 비용 및 위험이 수반되며 심할 때는 차량이 손상될 수 있다. 그러므로 무인 주행 중 발생할 수 있는 상황에 대한 다양한 시나리오와 실제 동특성을 반영한 로봇의 동역학 모델을 구성하여 실제 하드웨어를 운용시키지 않고도 동특성을 분석할 수 있는 실시간 시뮬레이터에 대한 개발이 요구된다. 실시간 시뮬레이터에 대한 많은 연구들이 진행됐지만, 대부분의 실시간 차량 시뮬레이터는 다양한 환경에서 안정적으로 실시간 해석을 하기 위해 차량 모델을 질점 동역학으로 모델링하거나 차량의 서스펜션을 간단한 함수형 서스펜션으로 구성하였다.
Yoo는 실시간 해석을 위해 현가장치 모델링을 무질량 링크로 고려하여 운동방정식의 크기를 줄였으며 무질량 링크 모델링에 현가 스프링이 장착되어 있는 연구를 진행하였다[1]. Gu는 실시간 차량 모델의 안정적인 해석 수행을 위해 상미분 방정식으로 표현할 수 있는 함수형 현가장치 모델을 개발하였으며 휠의 변위에 대한 현가장치의 상대변위를 함수식으로 표현하여 가상 시뮬레이터에 적용시켰다[2]. 이 경우 단순한 모델로 구성되어 있어서 해석 시간이 줄어들어 실시간성이 향상된다는 장점이 있지만 회전 거동에 대한 해석의 정확도는 떨어진다는 단점이 있다. Park은 휠로더의 주행 성능을 객관적으로 평가하기 위해 ODE를 통해 휠로더 모델을 구성하고 시뮬레이션을 수행하였다. 하지만 이는 물리 파라미터 간의 연결 유형을 간단하게 정의한 모델로 해석 시간은 빠르지만 정확한 동특성을 계측하기는 어렵다[3]. 정확한 동특성 확보를 위해 다물체 동역학 기반의 실시간 시뮬레이터에 대한 필요성이 증가하였다. 과거에는 다물체 동역학 모델로 실시간 해석을 진행할 경우 모델의 정확도는 향상되지만 계산량이 많아 실시간성이 떨어지는 문제가 있었다. 하지만 컴퓨터의 성능이 발전함에 따라 이전보다 신속한 계산이 가능해졌으며 차량모델을 간소화시킴으로써 실시간 해석이 가능한 수준까지 도달하였다.
본 연구에서는 무인 로봇차량의 정확한 동특성을 반영하기 위해 다물체 동역학 기반 실시간 원격주행 차량 시뮬레이터를 개발하는 것을 목표로 한다. RecurDyn을 통해 다물체 동역학 기반으로 모델링하고 MATLAB/Simulink 환경을 구성하여 실시간 통합 해석 시스템을 구성하였다.
2. 무인 로봇차량의 동역학 모델링
2.1 로봇차량의 동역학 모델링
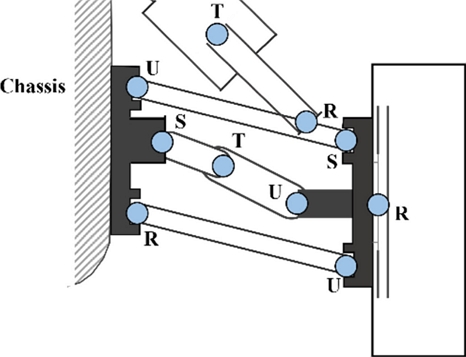
실험에 사용된 차량은 Fig. 1에 나타낸 WEGO 사의 Scout 2.0 모델을 사용하였다. Scout 2.0 모델은 원격 조종 및 무인 주행이 가능한 로봇이며 주로 실내가 아닌 외부에서 임무를 수행하는 로봇이다. 무인 로봇차량은 4개의 독립적인 서스펜션과 4개의 바퀴로 구성되어 있으며 각 바퀴는 인휠 모터(Inwheel Motor)를 통해 독립적으로 구동되도록 구성되어 있다. 각 바퀴의 속력 차이를 통해 조향을 하는 스키드(Skid) 조향 방식을 사용하고 있다. 본 연구에서는 무인 로봇차량을 모델링하기 위해 상용 다물체 동역학 프로그램인 RecurDyn을 활용하였으며, 무인 로봇차량은 1개의 차체와 4개의 서스펜션, 4개의 타이어로 모델링하였다. 무인 로봇차량의 서스펜션은 4개 모두 더블로커 현가장치(Double Rocker Suspension)의 구조를 가지고 있다. 서스펜션은 부싱요소가 사용되지만, 부싱 요소로 모델링 할 경우 실시간으로 해석을 수행하는 것이 어렵다. 그러므로 본 연구에서는 부싱요소 대신 조인트를 사용하여 무인 로봇차량의 기구학적 모델링을하였으며, 각 서스펜션의 조인트 모델링 정보를 Fig. 2에 나타내었다. Fig. 2에서 S는 구면 조인트(Spherical Joint), R는 회전조인트(Revolute Joint), U는 유니버셜 조인트(Universal Joint), T는 병진 조인트(Translational Joint)를 의미한다. 서스펜션은 2자유도를 가지고 있으며, 이는 바퀴를 구동시킬 수 있는 구동에 대한 자유도와 높이 방향의 구배에 따라 상하로 움직일 수 있도록 해 주는 수직 방향의 자유도이다. 무인 로봇차량 모델은 전체 14자 유도를 가진다.
본 연구에 사용된 무인 로봇차량의 서스펜션은 지면이 가해주는 충격 및 진동을 줄이기 위해 서스펜션에 스프링 및 댐퍼가 장착되어 있다. 서스펜션에 사용된 코일 스프링을 모델링하기 위하여 스프링의 CAD 정보와 재료 물성치를 활용하여 스프링의 특성을 정의하였다. 코일 스프링은 인장 및 압축 하중을 받게 될 때 와이어는 비틀림 응력을 받게 된다. 코일 스프링의 특성을 정의하기 위해 와이어가 받는 비틀림 응력을 기반으로 강성계수를 정의하였다[4-6]. 수식을 통해 유추한 스프링 강성계수와 적용된 댐핑 계수는 Table 1에 정리하였다.
2.2 로봇차량의 타이어 모델링
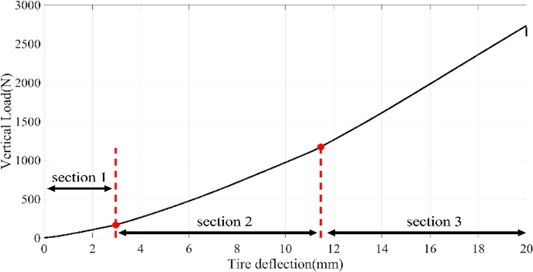
외부 환경에서 주행할 때 로봇차량에 들어오는 외력은 주로 지면으로부터의 가진력이다. 이 외력은 타이어와 로봇차량의 서스펜션에 의해 차체로 전달되기 때문에 정확한 타이어 파라미터를 확보하지 못한다면 실제 동특성을 파악하는 것이 어렵다. 본 연구에 사용된 무인 로봇차량에 적용된 타이어는 일반 승용 타이어가 아닌 Fig. 3과 같은 지름 310 mm와 높이 10 mm의 러그가 표면에 부착되어 있는 러그형(Lug-type) 타이어이다. 크기가 작고 러그를 가지고 있어서 차량동역학에서 주로 사용되고 있는 MF 타이어 모델과 같은 실험 타이어 모델을 쓰는 것은 불가능하여, 본 연구에서는 적은 변수를 사용하는 이론적 타이어 모델인 UA (University of Arizona) Tire[7,8]을 사용하였다. UA Tire 모델에 필요한 파라미터 중 타이어력에 가장 큰 영향을 미치는 수직 강성계수는 MTS의 만능 재료 시험기를 활용하여 계측하였다. 수직 강성계수는 타이어의 공기압에 따라서도 영향이 있으므로 시험 시 타이어의 공기압을 출고 기준인 40 psi로 세팅하여 시험을 진행하였다. Fig. 3에 나타낸 것처럼 시험기로 수직하중을 인가하였으며, 그때의 타이어 변형량을 측정하였다. 수직 강성에 대한 시험 결과는 Fig. 4에 나타내었으며 시험 결과를 보면 인가한 수직 하중 구간별로 크게 3가지의 수직 강성계수를 확인할 수 있다. 이는 러그형 타이어의 특성으로써 본 연구에 사용한 무인 로봇차량의 경우, 한 바퀴에 가해지는 수직력은 166.7 N이므로 이 구간에서의 수직 강성계수인 134.1 N/mm 사용하였다. 최종적으로 시험을 통해 정의한 수직 강성계수를 활용하여 UA Tire에 필요한 나머지 파라미터를 추정하였으며 마찰계수의 경우 선행연구[9]를 참고하여 일반적으로 사용하는 아스팔트 노면에 대한 마찰 계수를 사용하였다.
3. 통합 시뮬레이터 구성
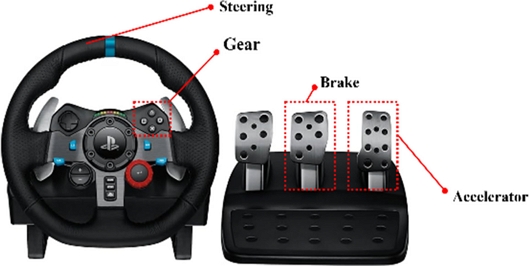
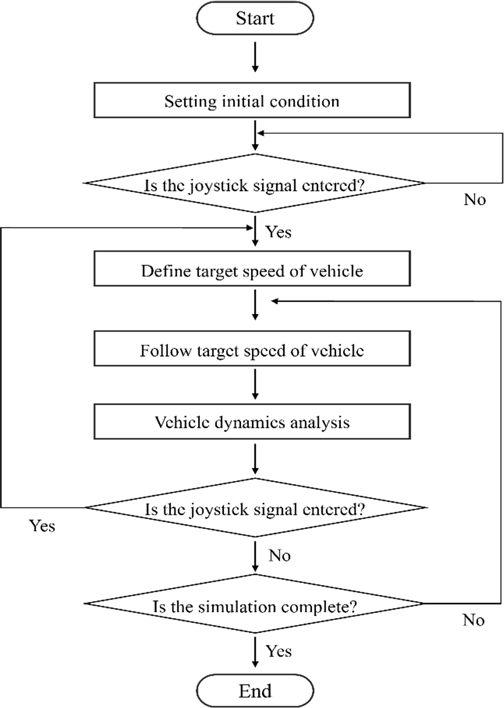
본 연구에서는 RecurDyn과 MATLAB/Simulink의 연성 해석 환경을 구성하여 실시간 원격 시뮬레이터를 개발하였다. 개발된 통합 시뮬레이터는 원격주행이 가능하며, 원격주행을 위해 Fig. 5의 Logitech사의 Wheel Joystick G29를 이용하였다. 시뮬레이터는 Fig. 6의 Flowchart 순서로 해석이 진행된다. 원격주행 환경을 위해 사용자는 조이스틱으로 구동 및 조향 입력을 넣어주게 되며 입력된 신호는 MATLAB/Simulink 환경으로 전달되어 차량이 명령에 맞게 주행할 수 있도록 토크 제어를 한다. 계산된 구동 토크를 RecurDyn 모델으로 전달하여 해석이 가능하도록 구성하였으며 사용자는 해석 결과를 실시간으로 확인하여 피드백 입력을 넣어준다.
3.1 MATLAB/Simulink 환경 구성
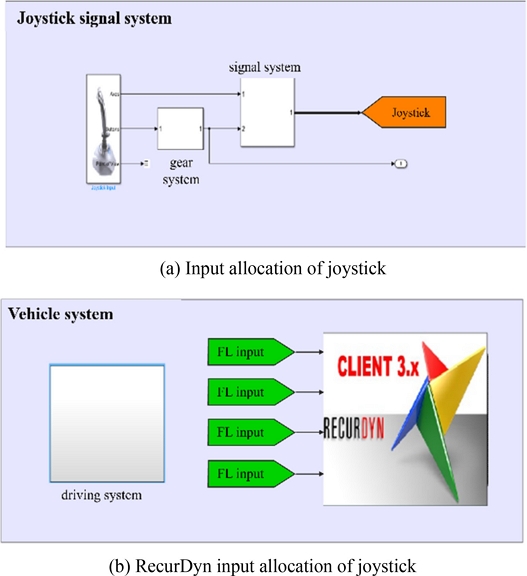
MATLAB/Simulink 환경은 조이스틱 신호를 정의하는 Joystick Subsystem, 정의된 신호를 차량의 스펙에 맞도록 연산을 하는 Driving System, 목표 속도를 추종하도록 구동 토크를 제어하는 Control Subsystem으로 구성하였다. Joystick Subsystem은 실제 차량과 같게 기어(Gear)에 따라 Driving, Parking, Neutral, Reverse와 같이 4가지 모드를 정의할 수 있으며 동일한 조이스틱 입력을 입력하더라도 기어 입력에 따라 출력되도록 구성하였다. 신호를 계산하게 되면 Driving Subsystem에서는 차량의 스펙에 맞도록 목표 속도를 계산하게 된다. 본 연구의 로봇 모델은 스키드 조향이기 때문에 조향 입력 및 가감속 입력 신호를 모두 고려한 후 각 바퀴의 목표 각속도를 연산한다. 마지막으로 Control Subsystem에서는 각 바퀴의 목표 각속도를 추종하도록 구동 토크를 제어할 수 있도록 구성하였다. 계산된 모터의 토크는 Co-simulation 환경을 구성하여 RecurDyn 모델로 전달이 가능하게 구성하였으며 전달받은 구동 토크 입력에 대하여 RecurDyn에서는 실시간으로 동역학 해석을 수행한다.
3.2 실시간 제어를 위한 PID 제어기 설계
본 연구의 실시간 원격 시뮬레이터는 사용자가 입력해 준 조이스틱 입력에 따라 각 휠의 목표 속도가 결정되며 각 휠의 토크를 제어하는 하위레벨의 PID 제어를 수행한다. PID 제어기는 비례 게인 값, 적분 게인 값, 미분 게인 값을 결정하여 정상상태 오차에 따른 피드백을 통해 원하는 값을 출력하는 제어방식이다[10]. 본 연구에서는 토크 제어시스템을 설계하여 실시간으로 4개의 휠의 목표 속도가 계산되면 현재 각 바퀴의 속도와의 비교를 통해 모터 토크를 조절하게 된다. 출력 토크 u(t)는 식(1)과 같이 4개의 각각의 바퀴(FL, FR, RL, RR)에 대하여 계산되어 차량 모델로 들어가게 된다. wd,FL 는 추종하고자 하는 1축 왼쪽 바퀴의 속도이며 wFL는 현재의 1축 왼쪽의 바퀴 속도를 의미한다.
| (1) |
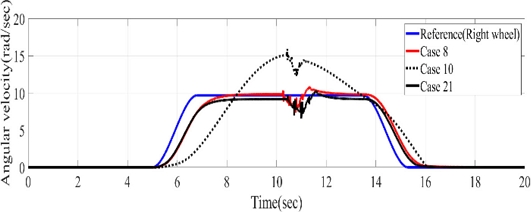
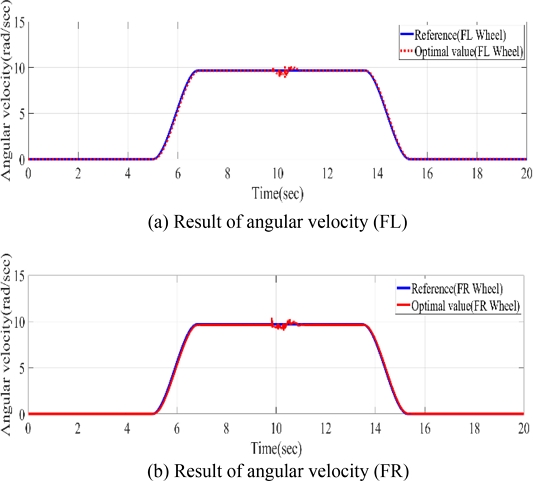
시뮬레이터에 구성된 PID 제어 시스템은 일정한 입력에 대한 제어를 하는 것이 아닌 실시간으로 변하는 조건을 충족시키는 제어를 수행해야 한다. 실시간 제어가 가능하도록 하기 위해서는 KP, KI, KD 값을 정의하는 것이 중요하다. 제어기의 성능 향상을 위해 Discrete Latin Hypercube Design 방법[11,12]으로 게인 값의 최적화를 진행하였다. 본 연구에서 제어기의 최종 목적은 정의한 목표 속도까지 0.1초 이내에 추종이 가능하여야 하며 과도한 Overshoot이 발생하지 않도록 하는 것이다. 설계 변수는 KP, KI, KD이며 3가지 설계 변수를 조절하여 제어기의 목적을 충족시킬 수 있는 게인 값을 정의하고자 하였다. 이때 제약조건을 두지 않은 채로 최적화를 시키게 되면 실제 성능에 적합하지 않은 게인 값을 설정하여 실제 모터의 성능을 넘어선 과도한 토크가 들어갈 수 있다. 실제 로봇의 각 바퀴에 장착된 인휠 모터의 최대 토크 성능은 27,625 N·mm이기 때문에 시뮬레이터에서 입력되는 구동 입력 토크의 최댓값이 최대 토크 성능을 넘지 않도록 제약조건을 설정하였다. 최종적으로 제어기의 성능을 평가하기 위한 목적함수는 목표 각속도와 현재 각속도의 RMS 오차와 과도한 오버슈트(Overshoot)가 발생하지 않도록 목표 속도와 현재 속도의 오차의 최댓값이 최소가 되도록 설정하였다. 각 목적함수의 중요도에 따라 가중치(Weighting)를 설정하여 식(2)부터 식(5)와 같이 목적함수를 정의하였다. xi는 각 시뮬레이션 스텝에서 계산된 각 바퀴의 각속도이며, xref는 추종해야 할 목표 각속도이다. 정의된 성능평가지수가 최소가 될 때 제어기의 성능은 최대라고 정의하였다. 가속, 감속, 외부의 충격에도 목표속도를 추종하는 것이 목적이기 때문에 최적화 시뮬레이션을 위한 주행 노면은 단순 장애물이 있는 노면 환경을 구성하였고 가속, 감속의 주행 조건을 설정하였다. DOE (Design of experiment)의 각 변수의 범위는 Table 3에 나타내었으며 범위내에서의 변수 조합에 따른 시뮬레이션 결과를 확인하였다. 변수 조합은 Table 2에 나타내었다. 각 바퀴의 인휠 모터에 장착된 최대 토크 성능을 초과할 경우 데이터에서 제외시킨 후 결과를 분석하였으며 Fig. 8은 각 변수 조합에 따른 각속도 추종 결과를 대표적으로 나타내었으며, 최적 게인 값을 적용했을 때의 바퀴 속도 추종 결과를 Fig. 9에 나타내었다. 바퀴 속도 추종 결과를 보면 10초 부근에서 바퀴의 속도가 공통적으로 불안정한 구간이 발생한다. 이는 10초 부근에서 외부의 충격 범프를 통과하면서 충격력을 받았기 때문이며, 충격에 의해 속도가 감소하였으나 다시 목표 속도를 빠르게 추종하는 것을 확인할 수 있었다. 결과적으로 가속, 감속, 정지, 외부 충격상황에서도 실시간 제어가 가능함을 확인할 수 있었다. 최종적으로 최적화된 PID 게인 값은 Table 3에 정리하였다. 최적화된 PID 게인 값을 적용시켰을 때 목표 속도에 비해 최대 0.04 rad/sec의 오차를 가지며 0.05초 이내로 시간 지연 없이 실시간으로 추종이 가능함을 확인하였다.
- Find
- a = Proportion Gain (KP)
- b = Intergral Gain (KI)
- c = Derivative Gain (KD)
to minimize
| (2) |
| (3) |
| (4) |
Subject to
| (5) |
3.3 실시간 시뮬레이터 환경 구성
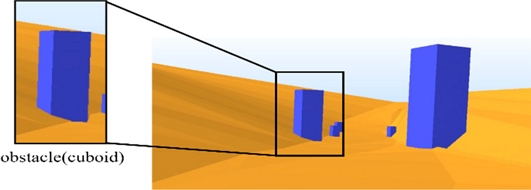
본 연구에서 실시간 원격 주행 시뮬레이터 알고리즘의 개발 및 검증을 위해 실제 조이스틱을 사용하여 실시간 시뮬레이션을 진행하였다. 실제로 차량에 탑승한 것과 같은 시야각을 구현하기 위해 Fig. 10에 나타낸 것처럼 차량 내부에서 노면을 바라볼 수 있도록 시야각을 설정하였다. 차량 시뮬레이터의 실재감 향상을 위해 차량의 모션을 반영한 시야의 흔들림을 구현하였다. 또한 실제 노면 환경을 모사하기 위해 사용자가 인식할 수 있는 장애물을 노면에 구성하였다. 장애물을 하나의 물체로 모델링할 경우 해석해야 할 구속 방정식이 늘어나기 때문에 해석 시간이 늘어날 수 있다. 본 연구에서는 실시간성을 확보하기 위해 운동방정식의 개수에 영향을 끼치지 않도록 지면(Ground)에 통합하여 모델링하였다. 실시간 원격주행 시뮬레이터와 실제 시간의 싱크를 맞추기 위해 샘플링시간(Sampling Time)을 조절하였으며 30초 시뮬레이션 대비 해석 시간의 시간지연이 발생하지 않음을 확인하였다. 주행 시뮬레이션 해석 데이터는 실시간으로 MATLAB/Simulink 환경으로 전달하게 되며 운전자는 실시간으로 차량의 동특성을 확인하면서 주행하는 것이 가능하다.
4. 실시간 주행 시뮬레이션 및 검증
4.1 시험 장비 및 시험 조건
실시간 주행 시뮬레이터를 검증하기 위해 주행 시험과 동일한 매뉴바를 입력하여 시뮬레이션을 수행하였다. 주행 시험은 로봇의 동특성을 계측하기 위해 휠엔코더와 IMU 센서를 활용하였다. 휠엔코더를 통해 인휠 모터의 각속도를 확인할 수 있으며 IMU 센서를 통해 로봇의 속도 및 가속도 데이터를 얻을 수 있다. 아스팔트 노면에서 범프 노면 주행 시험을 실시하였으며 범프 주행 시험에 사용된 범프는 일반 도로에서 사용되고 있는 폭 1,000 mm, 높이 75 mm의 범프를 사용하였다. 시험은 아스팔트 노면에서 차량은 최고 속력인 1.5 m/s까지 가속한 후 범프를 통과하였으며 Fig. 11는 범프노면을 지나고 있는 로봇을 나타내었다.
4.2 시험 및 주행 시뮬레이션 결과
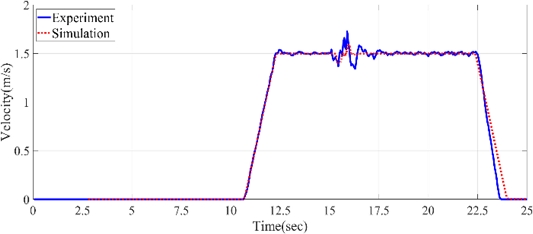
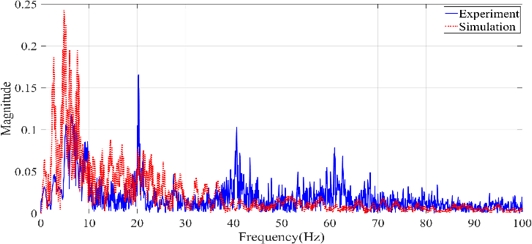
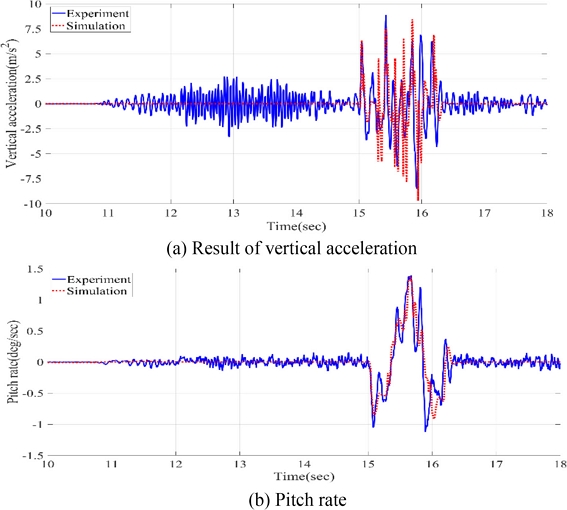
무인 로봇 모델의 검증을 위해 범프 노면 주행 시험과 실시간 원격 주행 시뮬레이션 결과를 비교하였다. Fig. 12는 동일한 조이스틱 입력을 넣었을 때 실험과 시뮬레이션의 차량의 속도를 비교하였다. 개발된 실시간 시뮬레이터는 시간지연 없이 조이스틱 입력에 따른 차량의 속도를 잘 추종하고 있으며 실제 차량의 스펙을 잘 반영하고 있음을 확인하였다. 또한 차량 모델을 검증하기 위해 범프 시험과 실시간 시뮬레이션에서 차체의 동특성을 비교 검증하였다. Fig. 13은 차체의 수직 가속도를 주파수 영역에서 비교한 결과이다. 실험의 1차, 2차 모드는 6.26, 20.36 Hz이며 시뮬레이션의 1차, 2차 모드는 5.12, 20.17 Hz임을 확인하였다. 실제 차량 결과와 비교하면 모드별로 1.14, 0.19 Hz가 차이가 발생하지만 오차의 크기가 작은 것을 확인할 수 있었다. 또한 실험에서의 수직 가속도는 40 Hz 이상의 고주파 대역이 확인된다. 40 Hz 대역의 주파수는 러그형 타이어에 의한 주파수임을 확인하였다. 시뮬레이션 모델은 러그형 타이어가 아닌 일반 UA 타이어 모델로 모델링하였기 때문에 고주파 대역의 주파수가 존재하지 않는다. 동일한 조건에서의 차량 모델 검증을 위해 실험의 고주파 대역에 대한 주파수를 모두 필터링한 후 크기 값을 비교하였다. Fig. 14에는 시험과 해석모델의 수직 가속도 및 Pitch Rate 결과를 비교하였다. 범프를 넘을 때의 수직 가속도와 Pitch Rate 데이터의 경향성은 일치함을 확인하였다.
5. 결론
본 연구에서는 실시간 원격주행 시뮬레이터를 개발하기 위해 RecurDyn과 MATLAB/Simulink의 연성해석(Co-simulation) 환경을 구축하였다. RecurDyn을 통해 무인 로봇차량의 동역학 모델을 확보하였으며 실제 로봇의 주행 데이터와 시뮬레이션 데이터의 비교를 통해 무인 로봇의 신뢰도를 확보하였다. 신뢰도가 확보된 동역학 모델과 MATLAB/Simulink와의 연성 해석 환경 구축을 통해 원격주행환경을 개발하였다. 개발된 연성해석 알고리즘은 사용자가 조이스틱의 페달을 밟거나 핸들링을 통해 조이스틱 신호를 MATLAB/Simulink 환경으로 전달하면 MATLAB/Simulink 환경에서 차량에 스펙에 맞게 연산 되어 목표 속도를 결정하고 목표 속도를 추종하기 위한 토크 제어 시스템이 실행되도록 하였다. 실시간으로 토크 제어를 하기 위해 최적의 게인 값을 도출하고자 하였으며 실험계획법을 통해 실시간 속도 추종이 가능한 게인 값을 정의하였다. 최종적으로 사용자의 조이스틱 입력에 대하여 실시간 원격주행이 가능한 시뮬레이터를 개발하였다. 개발된 시뮬레이터를 이용하여 실제 하드웨어를 사용하지 않고도 다양한 주행 조건에 대한 무인 로봇차량의 동특성을 실시간으로 분석하는 것이 가능하다. 현재 30초 시뮬레이션 시 시간 지연은 발생하지 않음을 확인하였으며, 향후 차량 모델이 변경되더라도 차량의 제원만 확보된다면 충분히 시뮬레이터에 적용시키는 것이 가능할 것으로 사료된다. 개발된 실시간 시뮬레이터를 통해 다양한 조건의 가상환경에서 차량을 주행시킴으로써 무인 로봇차량의 주행특성에 대한 데이터 베이스확보가 가능하여 자율주행 로봇의 제어 로직을 개발하는데 활용될 수 있을 것으로 사료된다.
NOMENCLATURE
| KP : | Proportion Gain |
| KI : | Integral Gain |
| KD : | Derivative Gain |
| wd, FL : | Desired Wheel Speed of a Front Left Wheel |
| wFL : | Current Wheel Speed of a Front Left Wheel |
| FL : | Front Left Wheel |
| FR : | Front Right Wheel |
| RL : | Rear Left Wheel |
| RR : | Rear Right Wheel |
Acknowledgments
이 논문은 부경대학교 자율창의학술연구비(2023년)에 의하여 연구되었음.
REFERENCES
- Yoo, W., Kim, K., Chung, B., Lee, J., (1999), Efficient vehicle modeling for real time simulation-effect of massless links with force element, Transaction of the Korean Society of Automotive Engineers, 7(4), 330-337.
- Gu, B., (2018), Functional real-time vehicle dynamics model for virtual reality vehicle simulator, M.Sc. Thesis, Chungnam National Univesity.
-
Park, J. W., Park, S. S., (2018), Evaluate of driving performance of wheel loader in the framework of Fitts’ law, Journal of Korean Society for Precision Engineering, 35(5), 499-506.
[https://doi.org/10.7736/KSPE.2018.35.5.499]

-
Lee, D.-W., Sohn, J.-H., Yoo, W.-S., (2014), Mass effect analysis is of a coil spring for the performance evaluation of a gas insulated circuit breaker, International Journal of Precision Engineering and Manufacturing, 15(12), 2543-2548.
[https://doi.org/10.1007/s12541-014-0625-1]

-
Oh, S. H., Choi, B. L., (2014), Analytical and experimental study for development of composite coil spring, Transactions of Korean Society of Mechanical Engineers A, 38(1), 31-36.
[https://doi.org/10.3795/KSME-A.2014.38.1.031]

- Lee, D., (2015), Design optimization of a coil-spring for a high voltage circuit breaker, M.Sc. Thesis, Pukyong National University.
- Lee, M., (1997), Development of a UA tire model for the automobile dynamics program AUTODYN7, M.Sc. Thesis, Pusan National University.
- Gim, G., (1988), Vehicle dynamic simulation with a comprehensive model for pneumatic tires, Ph.D. Thesis, The University of Arizona.
-
Lee, B.-G., Oh, S.-M., (2006), Study on friction characteristic for automotive tires, Journal of the Korea Academia-industrial Cooperation Society, 9(6), 1535-1540.
[https://doi.org/10.5762/KAIS.2008.9.6.1535]

-
Shin, S.-H., Han, S.-S. Geem, Z. W., (2021), PID speed control of BLDC motor with harmony search algorithm based on ziegler-nichols step response method, Journal of Korean Institute of Intelligent Systems, 31(3), 258-264.
[https://doi.org/10.5391/JKIIS.2021.31.3.258]

-
McKay, M. D., Beckman, R. J., Conover, W. J., (1979), A comparison of three methods for selecting values of input variables in the analysis of output from computer code, Technometrics, 21(2), 239-245.
[https://doi.org/10.1080/00401706.1979.10489755]

- RecurDyn V9R5, (2021), Discrete Latin Hypercube Design, https://dev.functionbay.com/RecurDynOnlineHelp/V9R5/index.html#!Documents/discretelatinhypercubedesign.htm

Graduate Student of Department of Mechanical Design Engineering at Pukyong National University. Her research interests are vehicle dynamics and multibody system
E-mail: suhyun1120@pukyong.ac.kr

Professor of Department of Mechanical Engineering at Pukyong National University. His research interests are mechanism design and multibody dynamics
E-mail: jhsohn@pknu.ac.kr

Professor in the School of Mechanical Engineering, Shandong University. His research interests are mechanical system design, marine towing system, floating wind turbine and vehicle dynamics
E-mail: xqzhu@sdu.edu.cn