광학창 표면형상 모델링 기반의 몬테카를로 시뮬레이션을 통한 광성능 연구
1국방과학연구소Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
As system performance continues to improve at higher resolutions, it becomes increasingly important to establish standards for imaging degradation caused by optical windows. In this study, random surface shapes were simulated on large area optical windows with peak-to-valley (P-v) values of 0.25, 0.5, and 1.0 λ. Modulation Transfer Function (MTF) values were derived for 1,000 cases per P-v value using Monte-Carlo simulations. The specifications achieved a surface accuracy of 0.5 λ and a parallelism of 0.01 mm. MTF measurements showed that the system MTF was 13.5% prior to the installation of the optical window, and 13.1% after installation. This indicates a degradation rate of approximately 3%.
Keywords:
Optical window, Surface form error, Monte-Carlo simulation, Interferometer, Modulation transfer function, Interference fringe키워드:
광학창, 면형상, 몬테카를로 시뮬레이션, 간섭계, 변조 전달 함수, 간섭무늬1. 서론
광학 시스템에서 광학창은 카메라 내부와 외부환경을 분리시키는 역할을 한다. 기계적으로는 외부환경에 견딜 수 있는 내구성을 지녀야 하며 광학적으로는 운용 파장 대역에서 충분한 투과율을 가져야 한다. 광학창을 통해 들어온 빛을 카메라가 집광하여 영상신호로 만들기 때문에 광학창에 의한 빔질의 영향이 최소가 되어야 한다. 광학창은 평판이기 때문에, 일반적인 광학시스템에서는 광학성능 저하에 큰 영향을 주지 않았다. 그러나 시스템 성능이 고해상화로 발전하면서 광학성능 할당 한계 때문에 광학창에 의한 결상특성 저하에 대한 성능규정이 필수적이다[1]. 이러한 이유에서 최근 다양한 측정 연구 사례가 발표되고 있다. 광학창을 통과한 슬릿빔의 휘어짐 정도를 가지고 왜곡 성능을 도출하여 광학창의 성능을 규정하는 방법[2], 광학창을 투과한 후 샥-하트만 센서에 입사되는 점들의 분포를 규정하는 방법[3], 광학창과 기계적 결합을 고려한 통합 광기계 해석을 통해 광학창 표면의 변화를 예측하여 반대 방향으로의 가공을 규정하는 방법 등 다양한 사례가 보고된다[4].
광학계의 결상 특성을 나타내는 데 일반적으로 사용되는 지표는 MTF (Modulation Transfer Function), RMS WFE (RMS Wavefront Error), Strehl Ratio, Rayleigh 1/4 Wave Rule, Encircled Energy, RMS Spot Size 등이 있다[5,6]. 가장 보편적으로 사용하고 있는 광학계의 해상력 검사 방법은 MTF 측정법이다. MTF는 물체의 Modulation (Contrast)를 광학계가 얼마나 정확하게 상(Image)에 전달하는가를 표현하는 함수이다. 주어진 공간주파수에서 측정된 MTF 값으로 평가를 한다. 이 방법은 광학계의 특성을 쉽게 파악할 수 있어 결상 특성을 검사할 때 보편적으로 사용하고 있다.
최종 광학계의 MTF를 예측하는 가장 기본적인 모델은 MTF 효과가 계속적으로 반영된다는 모델로, 각종 요인에 의한 MTF 변화량을 계산하고 이들의 곱으로 최종 MTF를 예상하는 것을 의미한다. 수차가 존재하는 광학계의 MTF를 구하기 위해서는 광학계의 회절 MTF (MTFdiff-optics)와 수차 MTF (MTFaberration), 두 개의 MTF의 곱으로 식(1)과 같이 표현한다[7].
| MTFoptics =MTFdiff-optics ×MTFaberration | (1) |
실제 렌즈 시스템에서 대부분 수차를 포함하는 MTF 산출식은 Shannon에 의해 제안된 식(2)와 같은 경험식을 사용한다[8].
| ATF=1-(Ws0.18)2×[1-4⋅(v-0.5)2] | (2) |
Ws는 파장의 비율로써 표현되는 RMS (Root Mean Square)파면 오차이다. 이것은 전형적으로 제작 과정에서 발생하는 파면 오차를 표현한다.
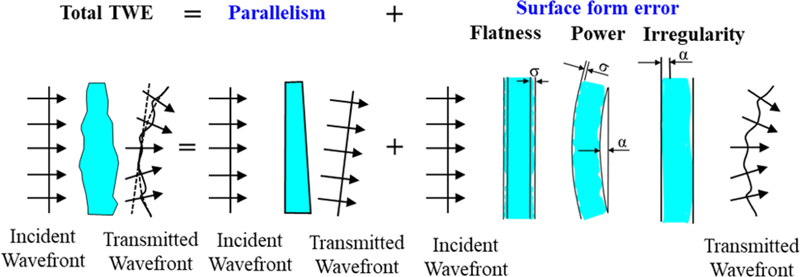
광학창의 경우 입사된 파면에 대해 상면에서 왜곡된 파면으로 변화하는 데 기인하는 주요 인자는 Fig. 1과 같다. Parallelism은 평행도라고 불리며 창의 치수 가공에 기인한다. Surface Form Error는 창의 형상 가공에 기인한다[9-11].
형상 가공 조건은 파장에 대한 크기로 표기되며, P-v (Peak to Valley) Error, RMS Error (≈ 0.25 × P-v Error) 값으로 성능을 규정한다. 면형상정도의 가공수준을 나타내기 때문에 광학계 성능과 직결되는 항목이다.
최근 연구되는 고해상 대면적 광학창의 경우 제작 전 광학성능 규정(WFE, Wedge Angle, Flatness, Power, Irregularity 등등) 없이 가공된 제품을 광학계에 장착했을 때 광학계 성능(MTF, WFE 등등)이 저하되는 문제가 빈번히 발생하는 사례가 많다. 즉, 광학창 제작 시 최적의 광학성능 보장을 위한 제작 규격을 정의하는 것은 매우 중요하다.
본 논문에서는 광학창 개발의 핵심규격인 면형상 정도를 나타내는 P-v Error 값을 0.25, 0.5, 1.0 λ인 경우에 대해 Code-V를 이용하여 랜덤 모델링하였다. 각 P-v Error 값이 나오는 랜덤모델링된 표면 형상정도를 1,000번 생성한 후 각각의 표면형상에 따른 광성능을 도출하였다. 이를 통해 광학창 제작을 위한 표면형상 규격을 도출한다. 도출된 규격으로 제작된 광학창에 대해서 광학계 장착 전·후의 MTF를 측정하여 시뮬레이션의 타당성을 검증하였다.
2. 광학창 해석 및 제작사양 도출
2.1 형상
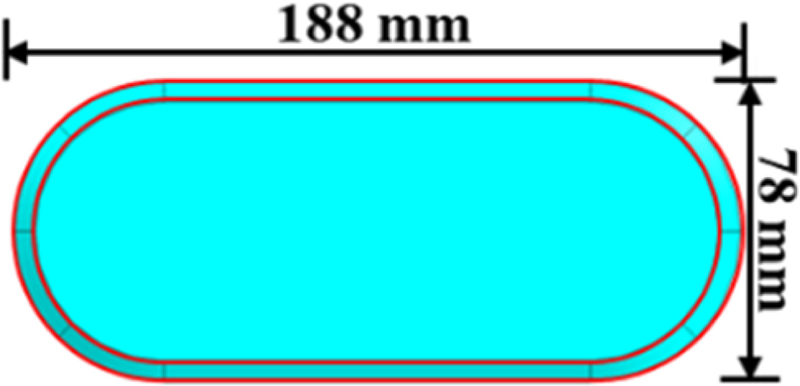
김발 구조(Gimbal Type) 및 광학계 경로를 고려하여 선정된 광학창 사이즈는 가로 188, 세로 78, 두께 5 mm이다. 소재는 사파이어(Sapphire)이다.
2.2 광학창 면형상 오차에 의한 MTF 영향성 해석
광학 시스템의 목표 MTF는 Fig. 3에서 보이는 것과 같이 10.8% 이상이다. 시스템 MTF는 광학창 MTF, 광학조립체 설계 MTF, 조립·정렬 MTF, 환경영향성 MTF의 곱으로 정의하였다. 요구 성능을 만족하기 위한 광학창의 성능저하 비율은 3% 미만의 MTF 저하를 보장해야 한다[12].
앞 절에서 언급하였듯이 광학창 가공 시 치수가공과 형상 가공 정도를 정의해야 한다. 먼저 치수가공의 항목인 평행도는 앞면과 뒷면의 두께 차이로 정의할 수 있으며 가공 기술을 고려하여 편차가 0.01 mm 이내로 정의하였다.
형상 가공 항목의 경우, 파장에 대한 비율 값으로 표기되며 간섭계를 이용한 측정방법이 가장 널리 사용된다. 원기(Reference Plate)와 시편(제작품)에서 나오는 파면의 차를 간섭무늬로 나타낸다. 이를 이용하여 면형상정도(Surface Figure Error)를 나타내는 P-v Error, RMS Error(≈ 0.25 × P-v Error)를 이용해 Flatness, Irregularity, Power 값이 도출된다. 간섭계는 특정 그리드 사이즈에서 포인트별로 들어오는 값들의 변형정도를 계측하여 간섭무늬로 보여준다. 이를 ASCII 포맷으로 정의하여 Code-V 프로그램을 이용하여 원하는 P-v 값을 모델링할 수 있다. P-v 값은 최종 결괏값이다. P-v 값은 원론적으로 보면 파면형상의 높은 곳과 낮은 곳의 길이이다. 그러므로 같은 P-v 값이 나온다고 해서 동일한 형상은 아닐 수 있다. 즉 동일한 P-v 값을 갖는 면형상은 셀 수없을 만큼 다양하다고 할 수 있다. 원하는 요구성능의 MTF를 만족하는 광학창의 면형상정도의 수준을 정의하기 위하여 광학창 면에 P-v 값은 같지만 형상은 랜덤으로 모사하여 입히는 방법을 적용하여 수천, 수만번의 케이스에 대해 MTF 값을 도출한다면, 요구성능을 만족하는 MTF에 해당하는 광학창의 면형상정도를 도출할 수 있다.
광학창 면형상정도에 의한 광성능 예측 방법은 Fig. 4와 같다. 광학창의 평행도는 0.01 mm, P-v Error 값은 (1) 0.25, (2) 0.5, (3) 1.0 λ 인 경우에 대해 랜덤 모델링을 한다. 각 P-v Error 값이 도출되는 면형상을 1,000번의 모델링을 수행한 후 각각의 형상정도가 MTF에 어떠한 영향을 주는지 확인한다. 광학창 없이 설계된 광학계만의 MTF를 이상적인 경우로 정의하고, 광학계전단에 위치한 광학창에 랜덤 모델링된 면형상정도를 적용하여 MTF 성능을 확인한다. 광학창이 있을 때와 없을 때의 MTF 값을 비교하면 광학창의 면형상 정도가 MTF 성능저하에 미치는 영향을 알 수 있다.
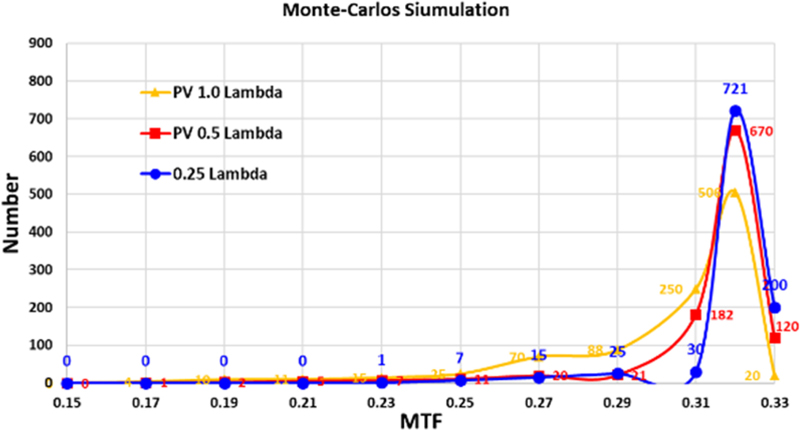
랜덤 모델링된 P-v Error 값이 적용된 간섭무늬 중 대표적인 그림은 Table 1과 같다. 광학조립체 설계 MTF는 33 LPS/mm (나이키스트 주파수)에서 0.33 이다. Fig. 3에서 광학창에 의한 MTF 저하율을 3% 이내로 정의하였기 때문에 해석 시 요구되는 기준 MTF는 0.32가 된다. 설계된 광학계 전단에 위치한 광학창면에 P-v Error 0.25 λ 적용 시, 1,000번의 해석 중 92.1%(921/1,000) 확률로 0.32 이상의 MTF 값을 보인다. 나머지 7.9%(79/1,000번) 확률로 MTF 0.32 이하이다. P-v Error 0.5 λ 적용시 1,000번의 해석중 79% 확률로 0.32 이상의 MTF값을 보였다. 나머지 21%는 MTF 0.32 이하이다. P-v Error 1.0 λ 적용시 1,000번의 해석 중 52.6% 확률로 0.32 이상의 MTF 값을 보였다. 나머지 47.4%는 MTF 0.32 이하이다.
해석 결과 P-v Error 0.25 λ 수준으로 정의함이 타당하다. 대면적의 광학창을 가공한다는 측면에서 P-v 0.25 λ 수준으로 제작하는 것은 기술적 난도의 상승과 더불어 시간적 비용적 손실이 많이 발생하게 된다. P-v Error 값을 정의하기 위하여 제작 후 측정되는 영역을 고려한다. 해석 시 P-v Error 값 도출을 위해 적용한 구경은 광학창 사이즈를 모두 포함한 영역이다. 그러나 광학창 제작 후 간섭계로 측정되는 구경은 100 mm 수준이다. 즉, 실제 제작 후 측정되는 영역은 시뮬레이션에서 정의한 영역보다 작기 때문에 해석 결과보다 좋은 값을 보일 것이다. 이로 인해 MTF 저하도 적을 것으로 판단된다. 이를 근거로 제작성이 쉽고, 시간적 비용적 소모도 적게들 수 있는 P-v Error를 0.5 λ 수준으로 성능규정을 정함이 타당하다.
2.3 광학창 제작결과
앞선 해석 결과에서 도출된 제작 사양은 평행도 0.01 mm 이하, P-v Error 0.5 λ 이하이다. 본 절에서는 제작 사양으로 가공된 광학창에 대한 제작결과를 기술한다. 첫 번째로 광학창의 면형상정도는 간섭계를 이용하여 파면을 측정하는 방법을 이용한다[13-15]. 광학창의 면형상 정도를 측정하는 방법은 2가지가 있다. 첫 번째 방법은 간섭계에서 발생하는 기준파면이 창의 앞면에 반사되어 돌아오는 파면과 뒷면에 반사되어 돌아오는 파면을 각각 측정하는 방법이다. 창에 코팅(무반사 코팅)이 되어있을 경우 앞면과 뒷면 파면의 측정이 어려운 단점이 있다. 두 번째 방법은 간섭계에서 투과된 기준파면이 광학창을 투과하여 기준거울을 맞고 돌아오는 파면을 측정하는 방법이다[16,17]. 본 연구에서 제작된 광학창의 면형상 정도 측정은 두 번째 방법을 이용하며 Fig. 6과 같다.
측정 시 사용된 간섭계의 구경은 100 mm이다. 광학창 면적이 간섭계 구경보다 크기 때문에 광학창 전 영역을 한번에 측정하기는 어렵다. 이러한 점을 감안하여 광학창 중심은 100 mm 범위로 측정하고 좌, 우는 70 mm 범위로 측정하여 전체 영역에 대한 면형상정도를 확인할 수 있도록 하였다. 측정결과 Table 2와 같다. 중심영역에서의 P-v 값은 0.501, 왼쪽 영역에서의 P-v 값은 0.517, 오른쪽 영역에서의 P-v 값은 0.525 λ이다.
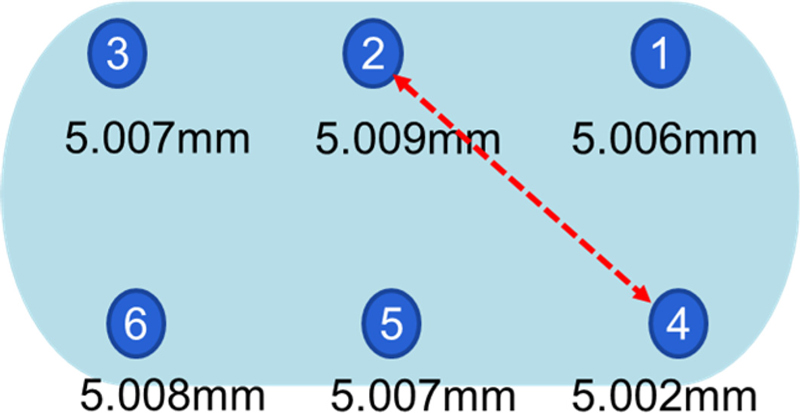
두 번째로 광학창의 평행도는 Fig. 7과 같이 디지털 고분해능 두께 측정기(분해능: 0.001 mm)를 이용하여 제작된 창의 각 6개 지점에 대한 두께를 측정하여 최댓값과 최솟값의 차이를 비교하여 평행도를 산정하는 방법을 이용한다. 측정 결과 0.007 mm이다.
3. MTF 측정
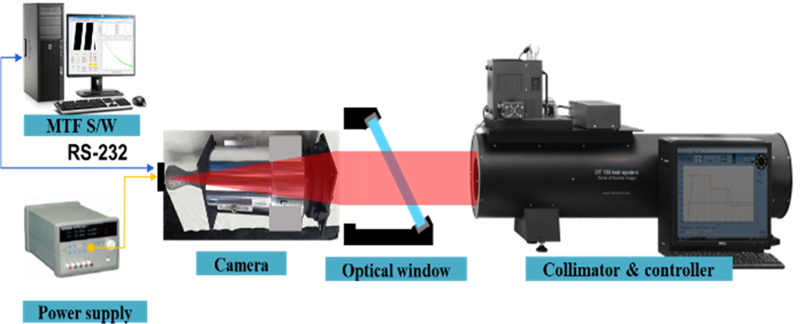
광학창의 MTF 측정을 위해 사용되는 측정장치는 시준기와 광학계이다. 시준기는 원거리의 영상을 모사하는 장치이다. 즉 평행광을 모사해 주는 장치이다. 시준기에 장착된 블랙바디 광원에서 출사된 적외선 빔은 광학계에 입사 되어 검출기에 초점을 맺는다. 이때의 MTF 값을 측정한다. 제작된 광학창을 광학계 앞에 장착한다. MTF 측정을 위해 장착된 카메라는 중적외선파장 대역(3-5 um)을 사용하며 F/수 4.0, 화각 1.2° × 1.2°, 화소수 256 × 256 이다. 광학창 장착 전, 후의 MTF 값을 비교하면 광학창에 의한 MTF 저하 정도를 알 수 있다. 실험에 사용된 시준기는 검교정이 완료된 INFRAMET 사의 CDT 660이다. 사양은 Table 3과 같다. Fig. 8과 같이 측정장비를 구성하였다.
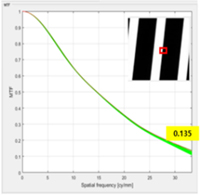
측정 결과 광학창 장착 전의 MTF는 13.5%이다. 광학창 장착후 MTF는 13.1%이다. 광학창에 의한 MTF 저하율은 3% 수준이다. 앞 절에서 할당한 광학창에 대한 MTF 저하 3% 미만의 목표성능을 충족한다.
4. 결론
본 연구에서 대면적 광학창에 의한 MTF 저하는 3% 이내를 목표로 한다. 이를 위해 대면적 광학창 면에 평행도 0.01 mm, P-v 값 0.25, 0.5, 1.0 λ를 보이는 랜덤형상을 모사하여 각 P-v 값별로 1,000가지의 케이스에 대해 MTF 값을 도출하였다. 결괏값을 반영하여 제작 사양은 면형상정도 0.5 λ, 평행도 0.01 mm 이하로 정의하였다. 도출된 제작 사양으로 제작된 광학창에 대해 MTF 값을 측정하였다. 제작된 광학창을 광학계 앞에 장착하는 경우와 미장착하는 경우의 MTF 값을 측정하였다. 광학창 장착 전 광학계의 MTF는 13.5%이고, 광학창 장착 후 시스템 MTF는 13.1%이다. 광학창에 의한 MTF 저하는 3% 수준으로 매우 작은 것을 확인하였다. 시스템에서 할당한 광학창에 의한 MTF 저하율 3% 미만의 목표성능을 충족하였다. 본 연구를 통하여 광학창 제작 사양 도출 방법의 타당성 및 시스템 차원의 성능분석 시 충분한 정확도를 갖는다고 판단된다.
Acknowledgments
This work was supported by the Agency for Defense Development Grant Funded by the Korean Government(924012318).
References
-
Park, K.-W., Park, S.-Y., Kim, Y.-S., Kim, K.-H., Choi, Y.-S., (2012), Dual band optical window (DBW) for use on an EO/IR airborne camera, Journal of the Optical Society of Korea, 16(1), 63-69.
[https://doi.org/10.3807/JOSK.2012.16.1.063]

- Youngquist, R. C., Skow, M., Nurge, M. A., (2015), Optical distortion evaluation in large area windows using interferometry, Proceedings of the 14th International Symposium on Nodestructive Characterization of Materials, 20(9), https://www.ndt.net/search/docs.php3?id=18112
- Lee, J. Y., Lee, W. C., (2011), Lens surface measurement system by shack-hartmann sensor, Journal of Korean Institute of Information Technology, 9(7), 79-84.
- Gearhart, S. A., (1991), Image degradations of an aerodynamically shaped optical window, Johns Hopkins APL Technical Digest, 12(1), 81-85.
- Fischer, R. F., Tadic-Galeb, B., Yoder, P., (2008), Optical system design, 2nd edition, McGraw-Hill.
- Smith, W. J., (2007), Modern optical engineering, 4th edition, McGraw-Hill.
-
Mahajan, V. N., (1998), Optical imaging and aberrations, SPIE PRESS.
[https://doi.org/10.1117/3.265735]

- Hecht, E., (2015), Optics, 5th edition, Pearson.
- Mejía-Barbosa, Y., (2021), Fundamentals of optics an introductory course, SPIE PRESS.
- Delay, M., Perry, S. W., Kicher, J., Prabhat, P., (2018), Maximizing the performance of advanced microscopes by controlling wavefront error using optical filters. https://www.idex-hs.com/docs/default-source/white-papers/optical-filters/maximizing-the-performance-of-advanced-microscopes-by-controlling-wavefront-error-using-optical-filters.pdf?sfvrsn=fa2fa3cd_3
- Burge, J. H., (2016), Specifying Optical Components. https://wp.optics.arizona.edu/optomech/wp-content/uploads/sites/53/2016/08/10-Specifying-optical-components.pdf
-
Laporte, P., Schnetler, H., Rees II, P., (2016), An automated performance budget estimator: A process for use in instrumentation, Proceedings of the Modeling, Systems Engineering, and Project Management for Astronomy VII, 99110H.
[https://doi.org/10.1117/12.2232276]

-
Malacara, D., (2007), Optical shop testing, 3rd edition, Wiley.
[https://doi.org/10.1002/9780470135976]

-
Mahajan, V. N., (1998), Optical imaging and aberrations, SPIE PRESS.
[https://doi.org/10.1117/3.265735]

-
Jeong, H. B., Park, H. M. Joo, K.-M., (2022), Lateral shearing inteferometry based on a polarization grating for wavefront sensing, Journal of the Korean Society Precision Engineering, 39(4), 245-251.
[https://doi.org/10.7736/JKSPE.022.009]

-
Banishev, A., Wang, J., Bhowmick, M., (2017), Optical interferometry, IntechOpen.
[https://doi.org/10.5772/63683]

- Zygo, Transmitted Wavefront. https://www.zygo.com/applications/measurements/transmitted-wavefront

received his M.S degree in Laser & Optical Information Engineering from Cheongju university, Korea, in 2009. he is a senior researcher at Agency for Defense Development (ADD), the 1st R&D Institute. His research interests include EO/IR systems.
E-mail: pkw@add.re.kr

received his Ph.D. degree in the School of Mechanical Engineering from Chung-Ang University, in 2018. Now, he is a senior researcher at Agency for Defense Development (ADD), the 1st R&D Institute. His research interests include EO/IR systems.
E-mail: ghunb16@add.re.kr

received his Ph.D. degree in the Department of Electrical Engineering, Korea Advanced Institute of Science and Technology, in 2019. Now, he is a principal researcher at Agency for Defense Development (ADD), the 1st R&D Institute. His research interests include EO/IR systems.
E-mail: cykim05@add.re.kr