Experimental Study on Altitude Motion Control of Unmanned Waterpowered Aerial Vehicle Using Nozzle Rotation Mechanism

1. Introduction

In the past five years, the applications of manned water-powered aerial vehicles have expanded beyond the boundary of the entertainment fields, and begun to implement into the specialized tasks, especially firefighting, rescue, and exploration. However, as can be seen from Fig. 1 [1], the work of both controlling vehicle and performing tasks brings a challenge to operators. Together with low visibility, dense smoke, and extreme temperature, their safety is usually threatened. To reduce the risk for the involved people, unmanned water-powered aerial vehicles (UWAVs) have been gradually put into development [2-6]. Like the manned type, the fundamental structural framework of these vehicles includes three main parts: a water pump, a water hose, and a board unit. The principle of operation is that the pump supplies water to the board through the flexible hose. Besides, water is jetted out at the nozzles’ outlet on the head to generate water thrust to propel the system. Additionally, there is a so-called drive mechanism used to generate proper forces and torques from this thrust, aiming to fly the vehicle.

Fig. 1

Application of aerial water-powered vehicle in firefighting

In terms of structural design, it includes three types, which are weight-shifting [4], flow-regulating [5-7], and nozzle rotation mechanisms [2,3,7-11]. The first type uses one or more weights that slide on the head surface to adjust weight distribution, mimicking the rider’s behavior on the flyboard [12]. The second type uses multiple valves to regulate the water flow inside the head’s body so that the water thrust at the outlet nozzles can be adjusted. The final type rotates water-jet nozzles to change the direction of water thrust. Compared to the first two types, the third one outperforms in reducing vibration for the water hose and providing good controllability for the head unit [13]. However, they still have some disadvantages, such as the non-minimum phase phenomenon [7] and the very limited operating range of water-jet nozzles [2,3,8-11]. These drawbacks cause the mentioned vehicles to have low maneuverability. To overcome these disadvantages, Tri et al. [14] have investigated the UWAV using four water-jet nozzles that can be independently and widely rotated. Although this vehicle has a large angular orientation, its arrangement restricted the operating range of force, especially in the vertical axis. Therefore, the flight ability of this vehicle is predicted to be poor.

In terms of control strategies, many robust controllers have been adopted to manipulate the UWAVs, e.g. a linear servo controller [4], a nonlinear cascade sliding mode controller [5] and a robust composite controller [6]. Although the abovementioned control systems indicated robustness and tracking capabilities, their effectiveness has not been yet confirmed in reality. In practical experiments, several studies focused on investigating the fundamental movement of the UWAVs. For stabilization problems, a derivative controller [2,3,8,9], a proportional-derivative (PD) controller [10], and a robust H∞ [11] controller have been implemented for the water-powered aerial long continuum robot using multiple water-jet nozzles. However, the stability of this robot is low because of actuator saturation, i.e. the very limited operating range of nozzles in these cases. For tracking control problems, Liu et al. [7] have deployed the PD controller for a 3-DoF angular motion control system. However, the results have not been compared to any desired references. Thus, it is difficult to evaluate the control performance. Besides, Tri et al. [14] have proposed an integral super-twisting sliding mode controller incorporating an extended state observer to control the attitude of the UWAV using a nozzle rotation mechanism. The results demonstrated that the vehicle could preserve good stability and tracking performance. In the above-mentioned studies, the altitude motion tracking control of the UWAV has not yet been investigated. One can see that there are many inevitable influences such as hose fluctuation and interaction between the altitude and attitude motions. They may cause the vehicle to face resonance, leading to system instability.

Therefore, this paper proposes a vehicle using a nozzle rotation mechanism and designs a simple controller to regulate its altitude, roll, and pitch motions. Although our vehicle inherits the design of the concept of [14], it has a distinguished feature, i.e. the modification of the nozzle’s arrangement. This layout allows our vehicle to have a large range of vertical force distribution under a constant water flowrate. Thereby, the flight ability of the proposed system is expected to achieve good performance. A proportional-derivative-integral (PID) controller incorporating gravity compensation is deployed to manipulate the 3-DoF motion system. This controller is expected to drive the vehicle following a desired trajectory under the mentioned influences and external disturbances.

In summary, the main contributions of this study can be outlined as follows:

• − A mathematical model of the head assembly is derived to describe its altitude and angular motions.
• − A PID controller with gravity compensation is implemented to govern the 3-DoF motion of the vehicle.
• − Experiments are conducted to evaluate the flight ability and confirm the system’s dynamic characteristics.

The rest of this paper is organized as follows. Section II describes the structure and mathematical model of the proposed system. Section III presents the control system design. Section IV shows the experimental results. Finally, Section V outlines conclusions.

2. System Modelling

2.1 System Description

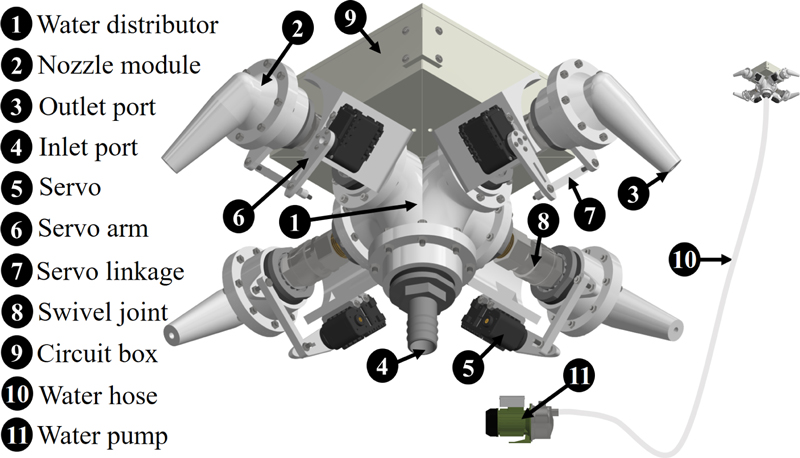
The overall structure of the vehicle and the notations of the head assembly can be described in Figs. 2 and 3, respectively. In particular, the proposed vehicle includes three main parts namely a water pump, a flexible water hose, and a head assembly. The pump is connected to the head by the hose, to supply the water to the main distributor. The flight ability of this vehicle depends on the water force distribution, i.e. a combination of the water thrust and the direction of nozzles. Initially, water, pressurized by the pump, flows through the water inlet port on the head assembly before jetting out from the four nozzle outlet sections. These outlet ports exhibit a significantly smaller cross-sectional area compared to the inlet port, designed to accelerate the water contained inside the distributor. Consequently, water thrust is generated, propelling the vehicle. Furthermore, a swivel joint placed between the water distributor and the nozzle module allows the nozzle to rotate. These nozzles are then driven by four servos at a 1:1 ratio through a servo arm and a servo linkage. Therefore, by controlling the direction of water thrust through four independently regulated nozzles, the proposed vehicle can achieve comprehensive 6-DoF motion.

Fig. 2

Conceptual design of the vehicle

Fig. 3

Coordinate definition and notations of the head assembly

In addition, four nozzles are spaced 90 [deg] apart from the vertical axis and angled 15 [deg] relative to the vertical plane, to improve stability. Furthermore, the servos are arranged such that the nozzles can be rotated from the horizontal plane to the downward direction. Thereby, the vertical force could be adjusted from zero to the maximum available thrust.

2.2 Mathematical Model of the Proposed UWAV

2.2.1 Kinematics Analysis

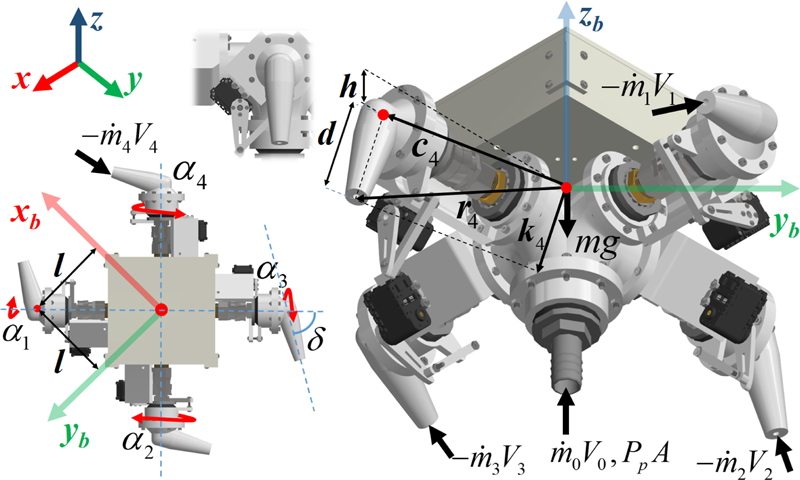
The body-fixed frame O_bx_by_bz_b [15] and Earth-fixed frame Oxyz [16] are used to describe the proposed vehicle in the 3- dimensional space. In the first coordinate system, the x-axis, y-axis, and z-axis follows the North, East, and upward directions, respectively. The latter coordinate is placed at the center of the mass of the vehicle, which its x_b-axis, y_b-axis, and z_b-axis point along forward, leftward, and upward directions, respectively. In addition, the kinematics of the 6-DoF vehicle can be described in the Earth-fixed frame, as follows:

$\[ \left[\begin{array}{c}v\\ \dot{\phi }\end{array}\right]=\left[\begin{array}{cc}{R}_b^E& O_3\\ O_3& T_b^E\end{array}\right]\left[\begin{array}{c}{v}_b\\ {\omega }_b\end{array}\right] \]$

(1)

where $$ \left(v={\left[\begin{array}{c}\dot{x} \dot{y} \dot{z}\end{array}\right]}^T,v_b={\left[\begin{array}{c}{\dot{x}}_b {\dot{y}}_b\hspace{0.25em}{\dot{z}}_b\end{array}\right]}^T\right)$$ are the translational velocities of the vehicle in the Earth and body frames, respectively; $$ \dot{\phi }={\left[\begin{array}{c}\dot{\varphi }\hspace{0.25em}\dot{\theta }\hspace{0.25em}\dot{\psi }\end{array}\right]}^T$$ are the Euler-angle rates (roll, pitch, and yaw rates); $$ {\omega }_b={\left[\begin{array}{c}{\omega }_{xb}\hspace{0.25em}{\omega }_{yb}\hspace{0.25em}{\omega }_{zb}\end{array}\right]}^T$$ are the body-axis rates. In addition, $$ \left(R_b^E,T_b^E\right)$$ are the rotation and transformation matrices, respectively.

As can be seen from Fig. 3, the position of the i^th (i = 1-4) nozzle’s outlet, $$ r_i={\left[r_{1_i} r_{2_i} r_{3_i}\right]}^T$$, is the sum of vectors k_i and c_i. In which, c_i is a vector with the origin placed at the center of the mass of the vehicle while its tail points to the center of rotation of the i^th nozzle. Besides, vector k_i, which describes the nozzle’s rotation part with a length of d, is derived from a sequence of rotations δ, α_i, and (-135 +90i) about the x_b-axis, y_b-axis, and z_b-axis, respectively. It is worth noting that α2 and α4 have a positive direction being clockwise. Additionally, the relative velocity of the jetted water at the i^th nozzle’s outlet with respect to the vehicle is denoted by $$ {\stackrel{-}{v}}_i$$, and is obtained in the same manner to k_i. Therefore, the position of the i^th nozzle’s outlet and the absolute velocity of the jetted water, $$ r_i={\left[v_{1_i} v_{2_i} v_{3_i}\right]}^T$$, are interpreted by:

$\[ \begin{array}{l}{r}_i=c_i+k_i\text{, }\\ v_i={\dot{r}}_i+{\stackrel{-}{v}}_i+v_b\\ k_i=R_i{\left[\begin{array}{c}0\hspace{0.25em}d\hspace{0.25em}0\end{array}\right]}^T,{\stackrel{-}{v}}_i=R_i{\left[\begin{array}{c}0\hspace{0.25em}{V}_i\hspace{0.25em}0\end{array}\right]}^T,\\ R_i=R_{-135+90i}^{Z_b}{\stackrel{-}{R}}_{{\alpha }_i}^{y_b}{R}_{-\delta }^{x_b}\text{, }\\ c_1={\left[\begin{array}{c}l\hspace{0.25em}l -h\end{array}\right]}^T,c_2={\left[\begin{array}{c}-l\hspace{0.25em}l\hspace{0.25em}-h\end{array}\right]}^T,\\ c_3={\left[\begin{array}{c}-l\hspace{0.25em}-l\hspace{0.25em}-h\end{array}\right]}^T,c_4={\left[\begin{array}{c}l\hspace{0.25em}-l\hspace{0.25em}-h\end{array}\right]}^T\end{array} \]$

(2)

Here, the term $$ R_{\left(\bullet 2\right)}^{\left(\bullet 1\right)}$$ represents the rotation matrix with $$ \left(\bullet 1\right)$$ and $$ \left(\bullet 2\right)$$ the rotation axis and the rotation angle, respectively; Vi denotes the axial velocity of the water flowing out at the i^th nozzle’s outlet. Moreover, the term $$ {\overline{R}}_{\left(\bullet 2\right)}^{\left(\bullet 1\right)}$$ is the rotation matrix of the nozzles about y_b-axis, and is written by:

$\[ {\stackrel{-}{R}}_{{\alpha }_i}^{y_b}=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\left({\left(-1\right)}^{i-1}\left({\alpha }_i-90\right)\right)& 0& \mathrm{s}\mathrm{i}\mathrm{n}\left({\left(-1\right)}^{i-1}\left({\alpha }_i-90\right)\right)\\ 0& 1& 0\\ -\mathrm{s}\mathrm{i}\mathrm{n}\left({\left(-1\right)}^{i-1}\left({\alpha }_i-90\right)\right)& 0& \mathrm{c}\mathrm{o}\mathrm{s}\left({\left(-1\right)}^{i-1}\left({\alpha }_i-90\right)\right)\end{array}\right] \]$

(3)

2.2.2 Dynamics Analysis

To begin with modeling, the following assumptions are made:

• − The mass of the nozzle module is lightweight.
• − The main contributor and its contained water volume are not deformable.
• − The water flow is frictionless and steady [17].

The head unit is mathematically described by Newton-Euler equations, as follows:

$\[ \begin{array}{c}m\left({\dot{v}}_b+{\omega }_b\times v_b\right)=F_b\\ J{\dot{\omega }}_b+{\omega }_b\times J{\omega }_b={\tau }_b\end{array} \]$

(4)

where m is the mass of the head with its contained water and J = diag{J_bx, J_by, J_bz} is the moment of inertia matrix. On the righthand side of Eq. (3), (F_b, τ_b) indicate the forces and torques acting on the head, they include the gravitation force observed from the body-fixed frame with g the gravitational acceleration, the water thrust force F_t and torque τ_t, and external disturbances (d_v, d_φ) such as wind gusts, ground effects, hose effects, etc. They can be written following:

$\[ F_b=F_t+m{\left(R_b^E\right)}^T{\left[\begin{array}{c}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}-g\end{array}\right]}^T+d_v,{\tau }_b={\tau }_t+d_{\phi } \]$

(5)

Moreover, the water thrust forces and torques can be obtained from the differential linear momentum equation, as follows:

$\[ F_t=-{\mathrm{\Sigma }}_{i=1}^4{\dot{m}}_i{v}_i-{\mathrm{\Sigma }}_{i=1}^4{\dot{m}}_i{\omega }_b\times r_i+{\left[\begin{array}{c}0\hspace{0.25em}0\hspace{0.25em}{\dot{m}}_0{V}_0+P_{p}A\end{array}\right]}^T \]$

(6)

$\[ {\tau }_t=-{\mathrm{\Sigma }}_{i=1}^4{\dot{m}}_i{r}_i\times v_i-{\mathrm{\Sigma }}_{i=1}^4{\dot{m}}_i{r}_i\times \left({\omega }_b\times r_i\right) \]$

(7)

where the terms $$ {\dot{m}}_0$$ and $$ {\dot{m}}_i$$ are the mass flowrates at the water inlet and outlet ports, respectively. Consequently, the axial velocities of the jetted water flowing through the inlet and outlet ports can be expressed in terms of flowrates, i.e. $$ V_0={\dot{m}}_0{\left(\rho A\right)}^{-1}$$ and $$ V_i={\dot{m}}_i{\left(\rho a\right)}^{-1}$$, where ρ represents the water density, A and a denote the cross-sectional areas of the inlet and outlet ports, respectively. The last term of Eq. (6), a consequence of isolating the head unit from the hose, indicates the acting force at the water inlet port under gauge pressure P_p. Additionally, in this stage, the difference in elevation and loss coefficient among the nozzles can be ignored, meaning the mass flowrates of the outlet ports are equal to each other and onefourth of the inlet flowrate.

In summary, by substituting Eqs. (5), (6), and (7) into (4), and using the kinematic relationship (1), the full dynamic equation of the proposed vehicle in the Earth-fixed frame can be achieved. However, as a first step to investigate the fundamental flight motions, the proposed vehicle is placed on the testbench, which is shown in Fig. 4, such that the longitudinal, lateral, and yaw motions are eliminated. Therefore, the 3-DoF vehicle can be derived as follows:

Fig. 4

Vehicle prototype on the testbench

$\[ \ddot{x}=H\dot{x}+Zu+g+d\text{,} \]$

(8)

where:

$\[ \begin{array}{l}x={\left[\begin{array}{c}z\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\varphi \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\theta \end{array}\right]}^T,H=Z\epsilon Z^{-1}-Z{\dot{Z}}^{-1},g={\left[\begin{array}{c}-g\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\end{array}\right]}^T\\ Z=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\varphi \mathrm{c}\mathrm{o}\mathrm{s}\theta & 0& 0\\ 0& 1& \mathrm{s}\mathrm{i}\mathrm{n}\varphi \mathrm{t}\mathrm{a}\mathrm{n}\theta \\ 0& 0& \mathrm{c}\mathrm{o}\mathrm{s}\varphi \end{array}\right],\epsilon =\left[\begin{array}{ccc}-{\dot{m}}_0{m}^{-1}& 0& 0\\ -l{\dot{m}}_0{\left(J_{bx}\right)}^{-1}& {\xi }_1& 0\\ l{\dot{m}}_0{\left(J_{by}\right)}^{-1}& 0& {\xi }_2\end{array}\right]\\ {\xi }_1=-{\dot{m}}_0{\left(J_{bx}\right)}^{-1}\left(h^2+l^2+2^{-1/2}dl\mathrm{c}\mathrm{o}\mathrm{s}\delta +2^{-1}\left(d^2+{\mathrm{c}\mathrm{o}\mathrm{s}}^2\delta \right)\right),\\ {\xi }_2=-{\dot{m}}_0{\left(J_{by}\right)}^{-1}\left(h^2+l^2+2^{-1/2}dl\mathrm{c}\mathrm{o}\mathrm{s}\delta +2^{-1}\left(d^2+{\mathrm{c}\mathrm{o}\mathrm{s}}^2\delta \right)\right)\end{array} \]$

(9)

and

$\[ \begin{array}{l}u=Q{\left[\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_1\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_2\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_3\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_4\right]}^T,Q=\left[\begin{array}{cccc}{q}_1& q_1& q_1& q_1\\ q_2& q_2& -q_2& -q_2\\ -q_3& q_3& q_3& -q_3\end{array}\right]\\ q_1=\frac{{\dot{m}}_0^2\mathrm{s}\mathrm{i}\mathrm{n}\delta }{16m\rho a},q_2=\frac{{\dot{m}}_0^2\mathrm{s}\mathrm{i}\mathrm{n}\delta }{16J_{bx}\rho a},q_3=\frac{{\dot{m}}_0^2\mathrm{s}\mathrm{i}\mathrm{n}\delta }{16J_{by}\rho a}\end{array} \]$

(10)

In the above formula Eq. (8), d represents the remaining terms after substitution and is considered as the disturbance. Additionally, the above mathematical model straightforwardly reveals that the proposed vehicle is nonlinear. Furthermore, the four controllable nozzles are used to drive the 3-DoF vehicle on the testbench, meaning the system is overactuated. One more thing, the presence of the nondiagonal elements in ε implies the proposed vehicle has an interaction between the altitude and attitude motions during the flight.

3. Control System Design

The objective of the control system is to drive the vertical position of the vehicle to follow the desired reference and to stabilize its roll and pitch angles at the equilibrium point with the smallest possible error. As a first step to address this objective, a PID controller is a proper choice because of its simplicity and intuitiveness in practical implementations.

Remark: In this system, the large-scale water pump causes unexpected issues such as low responsiveness and a lack of high precision, leading to significant delays in water thrust control. The most straightforward solution to overcome this is to keep the water flowrate constant. Thereby, the water force distribution of the vehicle depends on the nozzles’ angle.

Initially, let us define the error between the desired reference x_d = [z_d ϕ_d θ_d]^T and the plant output x as e = x_d - x. Moreover, assuming the desired reference x_d is once continuously differentiable, the control law is designed as:

where K_p, K_i, and K_d represent the controller’s gains, these gains are chosen such that the control system achieves stability. In the above formula Eq. (11), the first three terms in parentheses represent the PID controller, while the last term represents the gravity compensation. In which, the first term provides an immediate response to error. The second term eliminates the steady-state error by accumulating the difference between the desired reference and the actual plant output. The third term predicts the upcoming behavior of the error based on its rate of change. The last term compensates for the effect of gravity on the vehicle. Additionally, by substituting Eqs. (11) into (10), one gets the corresponding nozzle rotation angle vector α = [α₁α₂α₃α₄]^T based on the proposed control law:

with Q^† the right inverse of Q. It is worth noting that Q ∈ R^3×4 has linearly independent rows and its right-invertible matrix is given by Q^† = Q^T(QQ^T)^-1

4. Experiments

4.1 Experimental Setup

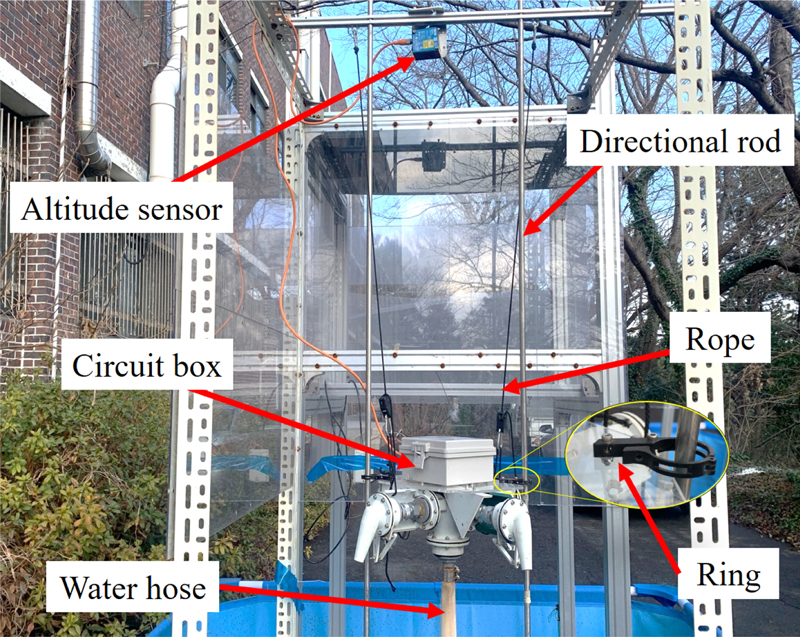
In this section, the experiments are conducted on the testbench to validate the flight ability and capture the dynamic properties of the proposed vehicle under practical conditions. As can be seen from Fig. 4, the vehicle is located atop the two directional rods on the testbench, positioned 1.3 m above the ground so that the longitudinal, lateral, and yaw movements can be eliminated. The detailed systematic parameters of the vehicle are presented in the following Table 1.

Table 1

Specification of the system

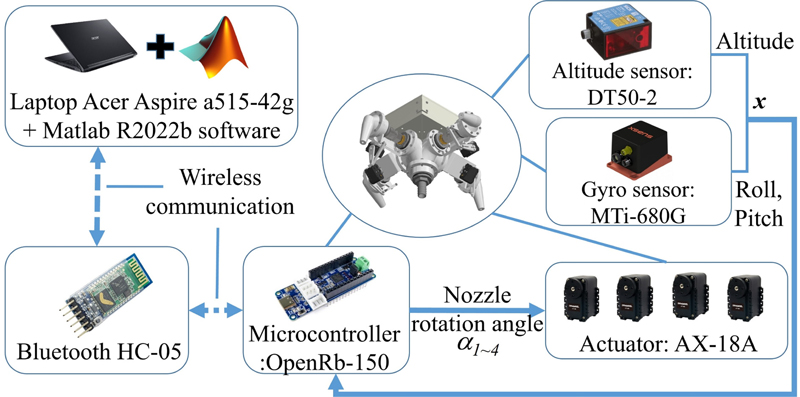
The experiment setup is outlined in Fig. 5. In detail, the proposed controller is deployed on a 32-bit OpenRB-150 microcontroller. Operating at a clock speed of 48 MHz, this microcontroller can provide the control system with a sample time of 0.01 s. Additionally, the HC-05 Bluetooth enables wireless communication between the vehicle and a laptop equipped with an AMD Ryzen 5500U processor, 32 Gb RAM, and an NVIDIA GeForce GTX 1650 graphics card. Moreover, the baudrate for both wireless and serial communication protocols in this system is synchronized at 921.6 Kbps. Moreover, Matlab R2022b software on the laptop handles the transmission of controller parameters and reception of data from the vehicle. On the other hand, there are two sensors used to realize the 3-DoF motion of the vehicle. The first, a DT50-2 sensor placed on the top of the testbench, measures the vertical position of the head assembly. The second sensor, an MTi- 680G located on the vehicle, measures the roll and pitch angles.

Fig. 5

Block diagram of experimental setup

4.2 Experiment Results

In this section, the tilt angles of the head assembly are stabilized at an equilibrium point while the altitude follows the desired complex trajectory with a peak-to-peak amplitude of 0.8 m. This scenario is conducted in 72 s and described as follows:

$\[ x_d={\left[\begin{array}{c}{z}_0+\stackrel{-}{z}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\end{array}\right]}^T \]$

(13)

where z₀ is an initial altitude placement above the ground and $$ \stackrel{-}{z}\hspace{0.25em}$$ varies over time t, which is given by:

(14)

Additionally, the PID parameters are obtained by the trial-anderror method, as follows: K_p = diag{21.5, 100, 100}, K_i = diag{2.5, 100, 100}, K_d = diag{0.5, 10, 10}. To come up with the proper control parameters, these steps are done: First, tune the proportional gain until the head assembly begins to oscillate. Then, add the integral gain to reduce steady-state error. Finally, select an appropriately small derivative gain to improve tracking performance.

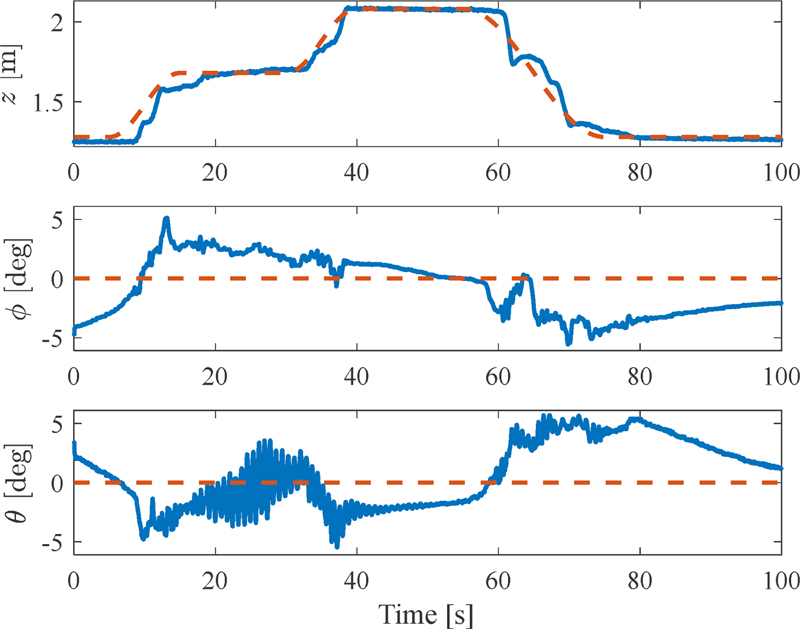
The fundamental flight motion of the vehicle within the first 72 s, namely takeoff, hovering, and landing, can be intuitively observed from Fig. 6. Especially, in the first stage a.1, the head assembly moves towards the balanced position, where the attitude angles equal zero. Then, the vehicle gradually takes off (stages a.2 to a.3) and hovers in the air at the first height of 1.3 m (stages a.3 to a.5) and then the second height of 2.1 m (stages b.6 to b.8), respectively. Finally, the vehicle lands on the ground (b.9 and b.10).

Fig. 6

Vehicle motion recorded during flight testing

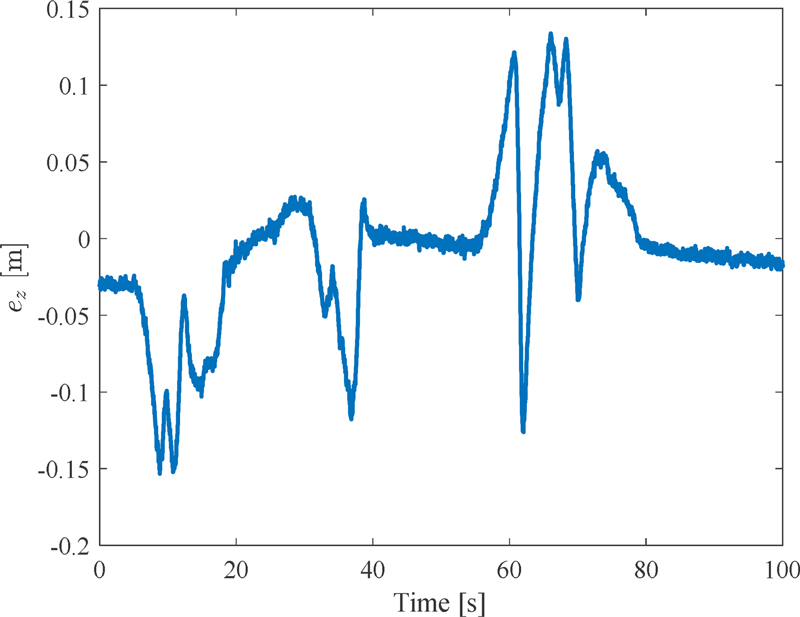
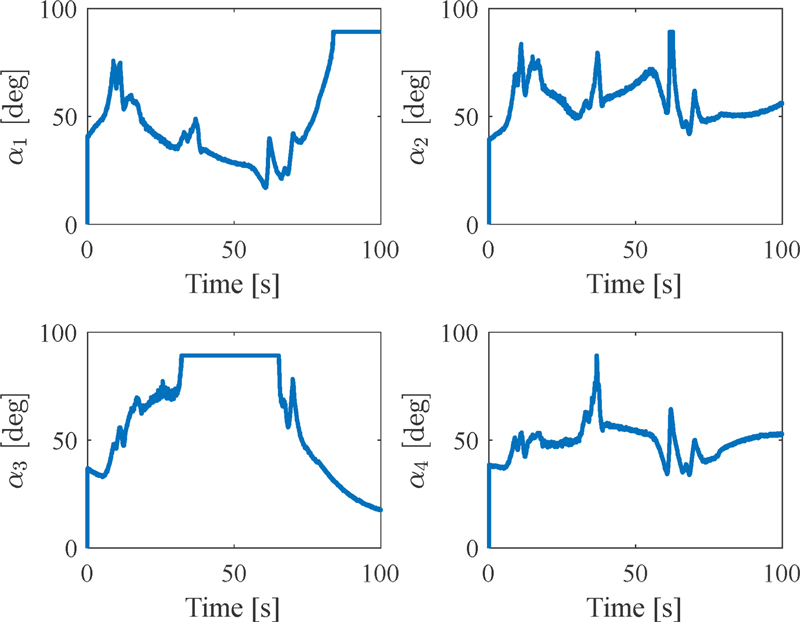
On the other hand, Figs. 7 to 9 have been provided for a comprehensive analysis of the vehicle’s flight characteristics. They are namely the motion control response of the vehicle, altitude tracking error, and control effort, respectively. Besides, note that the red dotted lines represent the desired references. In Fig. 7, one can see the PID controller can provide the system with fair stability and tracking performance. In detail, although there is a deviation from the equilibrium point at the beginning, the two roll and pitch angles of the vehicle can overall converge towards the origin by the end of the flight. Furthermore, the maximum angular oscillation amplitude is approximately ±5 deg, which falls within an acceptable range. On the other hand, the proposed vehicle can fly following the desired altitude reference with low tracking error, which can be realized clearly in Fig. 8. Additionally, the vehicle can hover in the air with very minor steady-state error observed from 40 to 55 s. In Fig. 9, at the start of takeoff, the position of the four nozzles rotates approximately 40 deg downward as a result of the gravity compensation part in the control law. Although the 1st and 3rd nozzles sometimes reach saturation at 90 deg, the overall control effort of these nozzles is consistently maintained at an average value.

Fig. 7

Motion control responses of the vehicle. The red dotted line is trajectory; the solid blue line is system response

Fig. 8

Altitude tracking error

Fig. 9

Control effort

However, some unexpected phenomena were observed during the flight testing. Firstly, the interaction between altitude and attitude results in fluctuations during the takeoff and landing processes of the vehicle. Besides, the large overshoots of the two angular motions are also captured, for instance, from 10 to 15 s and 60 to 75 s, respectively. Secondly, the impact of the water hose on the head assembly is evident. Especially, the water hose collides with the ground, therefore causing it to bounce at 63^rd s, resulting in altitude response overshoot. Furthermore, although the head assembly itself is a symmetrical structure, the entire system, including the water hose, is not. In this case, as can be seen from Fig. 6, the initial position of the water hose is almost on the O_bx_bz_b plane. Therefore, from 15 to 37 s, when the water jet hits the water hose, the hose will fluctuate and cause a vibration on the head assembly, especially in the longitudinal direction rather than the lateral direction. It is the main cause of oscillations in pitch motion more than roll motion.

5. Conclusions

This paper has proposed an unmanned water-powered aerial vehicle using a nozzle rotation mechanism and designed a simple 3- DoF controller to regulate its altitude, roll, and pitch movements. The vehicle aims to support the operators in specialized tasks around water bodies such as firefighting, rescue, and exploration. To achieve this, the mathematical model of the vehicle was first derived to realize its dynamic properties. They are namely nonlinearity, overactuation, and interaction between the altitude and attitude.

A well-known PID controller was then applied to govern the 3- DoF motion of the vehicle, namely altitude, roll, and pitch. The experiments were conducted to evaluate the flight capability and verify the dynamic characteristics of the proposed vehicle. The experimental results demonstrate that the vehicle can follow the desired trajectory under the influences of water hose fluctuation and the interaction between altitude and attitude.

In future work, to enhance the control performance of the system and overcome these influences, the following steps will be pursued: 1) modifying the driven mechanism to enable the nozzles to have an unlimited rotation range, and 2) applying a robust controller to compensate the vehicle’s dynamic properties and disturbances.

Acknowledgments

This work was supported in part by the National Research Foundation (NRF), South Korea, under Project BK21 FOUR (Smart Robot Convergence and Application Education Research Center); and in part by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIT) under Grant 2022R1A2C1003486.

References

• Dubai firefighters use jetpacks to aid high-speed response, euronews. https://www.youtube.com/watch?v=H1VIxUTzb1I
• Ando, H., Ambe, Y., Ishii, A., Konyo, M., Tadakuma, K., Maruyama, S., Tadokoro, S., (2018), Aerial hose type robot by water jet for fire fighting, IEEE Robotics and Automation letters, 3(2), 1128-1135. [https://doi.org/10.1109/LRA.2018.2792701]
• Ando, H., Ambe, Y., Yamaguchi, T., Yamauchi, Y., Konyo, M., Tadakuma, K., Maruyama, S., Tadokoro, S., (2020), Fire extinguishment using a 4m long flying-hose-type robot with multiple water-jet nozzles, Advanced Robotics, 34(11), 700-714. [https://doi.org/10.1080/01691864.2020.1769723]
• Dinh, C.-T., Huynh, T., Kim, Y.-B., (2022), LQI control system design with GA approach for flying-type firefighting robot using waterpower and weight-shifting mechanism, Applied Science, 12(18), 9334. [https://doi.org/10.3390/app12189334]
• Lee, D.-H., Huynh, T., Kim, Y.-B., Soumayya, C., (2021), Motion control system design for a flying-type firefighting system with water jet actuators, Actuators, 10(10), 275. [https://doi.org/10.3390/act10100275]
• Huynh, T., Kim, Y.-B., (2023), Motion control system design for a novel water-powered aerial system for firefighting with flowregulating actuators, Drones, 7(3), 162. [https://doi.org/10.3390/drones7030162]
• Liu, X., Zhou, H., (2019), Unmanned water-powered aerial vehicles: Theory and experiments, IEEE Access, 7, 15349-15356. [https://doi.org/10.1109/ACCESS.2019.2895335]
• Yamauchi, Y., Ambe, Y., Konyo, M., Tadakuma, K., Tadokoro, S., (2021), Passive orientation control of nozzle unit with multiple water jets to expand the net force direction range for aerial hose-type robots, IEEE Robotics and Automation Letters, 6(3), 5634-5641. [https://doi.org/10.1109/LRA.2021.3082019]
• Yamauchi, Y., Ambe, Y., Konyo, M., Tadakuma, K., Tadokoro, S., (2022), Realizing large shape deformations of a flying continuum robot with a passive rotating nozzle unit that enlarges jet directions in three-dimensional space, IEEE Access, 10, 37646-37657. [https://doi.org/10.1109/ACCESS.2022.3162835]
• Ambe, Y., Yamauchi, Y., Konyo, M., Tadakuma, K., Tadokoro, S., (2022), Stabilized controller for jet actuated cantilevered pipe using damping effect of an internal flowing fluid, IEEE Access, 10, 5238-5249. [https://doi.org/10.1109/ACCESS.2022.3140760]
• Maezawa, Y., Ambe, Y., Yamauchi, Y., Konyo, M., Tadakuma, K., Tadokoro, S., (2023), Translational disturbance rejection for jet-actuated flying continuum robots on mobile bases, IEEE Robotics and Automation Letters, 8(11), 7456-7463. [https://doi.org/10.1109/LRA.2023.3318189]
• Robinson, B., (2015), Water propelled flying board, US9145206B1.
• uynh, T., Lee, D.-H., Kim, Y.-B., (2023), Study on actuator performance evaluation of aerial water-powered system for firefighting applications, Applied Sciences, 13(3), 1965. [https://doi.org/10.3390/app13031965]
• Dinh, C.-T., Huynh, T., Lee, D.-H., Kim, Y.-B., (2023), Design and experiments of angular motion control for a novel unmanned water-powered aerial vehicle, IEEE Access, 11, 112719-112730. [https://doi.org/10.1109/ACCESS.2023.3324038]
• Niku, S. B., (2019), Introduction to robotics: analysis, control, applications, John Wiley & Sons.
• Khalil, W., Dombre, E., (2004), Modeling, identification and control of robots, Kogan Page Science.
• White, F. M., (2016), Fluid Mechanics, 8th edition, McGraw- Hill.