선형 모터 모션 스테이지의 맞춤형 전류 제어

1. 서론

21세기 4차 산업혁명 시대에 AI 기술이 발전하면서 반도체 회로의 집적도가 높아지고 수요가 폭발적으로 증가함에 따라 고성능, 고효율, 초정밀 반도체 생산 공정이 요구되고 있다[1]. 예를 들어, 반도체 노광 장비는 고속으로 이동하며 시간당 230장의 웨이퍼를 나노미터 단위의 정밀도로 처리해야 한다[2].

고속 고정밀 반도체 생산 공정 장비의 핵심 요소로서 고성능 모션 스테이지의 중요성이 부각되고 있다. 스테이지의 모션 성능 향상을 위해서는 위치 제어기뿐 아니라 정밀한 추력 생성을 위한 전류 제어기도 중요하다[3]. 간단한 구조로 외란을 추정하고 보상하는 외란 관측기(DOB)를 전류 제어에 적용하여 모델의 불확실성과 역기전력을 보상할 수 있다[4-6]. 하지만 스테이지 최종 성능 향상을 위해서 시스템 주파수 응답을 고려한 체계적인 전류 제어기 설계가 필요하다[7-9].

수동 반발력 보상(Reaction Force Compensation, RFC) 선형 모터 모션 스테이지는 자석 트랙 관성 에너지로 이동자 반발력을 소산하지만 모션 종료 후 자석 트랙 잔류 진동으로 이동자의 정착 시간과 미세 지터(Zitter) 증가 등의 성능 저하가 발생할 수 있다[10]. 모델 기반 외란 관측기를 모션 제어에 적용하여 반발력 보상 스테이지 성능 저하를 줄일 수 있다[11-12].

이 논문에서는 선형 모터 모션 스테이지의 위치 결정 성능 향상을 위한 맞춤형 전류 제어를 연구하였다. 먼저 에어 베어링으로 지지되고 수동 반력 보상 기능을 갖춘 560 mm 스트로크, 5 m/s 속도, 280 N 추력의 선형 모터 모션 스테이지를 구축하였다. Power PMAC 모션 제어기의 맞춤형 전류 제어 유저 코드를 개발하고 이를 선형 모터 모션 스테이지에 적용하였다. 맞춤형 전류 제어에는 d/q축 전류 제어기와 전류 외란 관측기가 포함된다. 모션 제어기에 가진 신호를 주입하고 전체 시스템 주파수 응답을 측정하고 이를 바탕으로 전류 제어기 이득을 조절할 수 있는 튜닝 GUI를 개발하였다. 전류 제어기 이득 조절 전후 Power PMAC 전류 제어기와 정적 및 동적 성능을 비교하여 그 효과성을 검증하였다.

2. 전류 제어 유저 코드 구현

2.1 시스템 구성

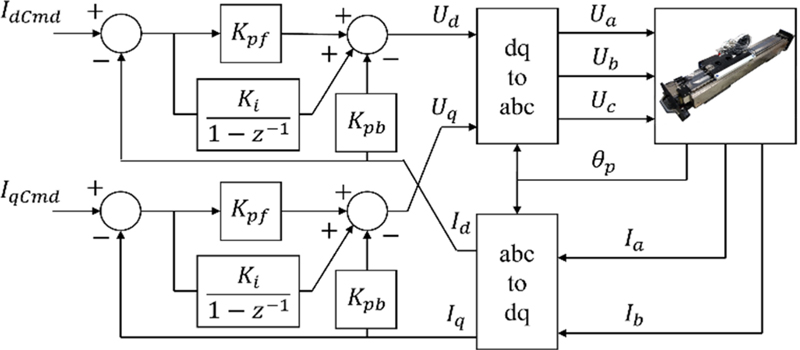
수동 반발력 보상 선형 모션 스테이지 모션 제어 시스템은 Fig. 1과 같이 공심형 선형 모터(Justek JTKL-3638), Direct PWM 드라이버(Servotronix CDHD-006), 상용 모션 제어기(PowerPMAC, ACC-24E3)로 구성되어 있다. 모션 스테이지는 최대 스트로크 560 mm, 최대 속도 5 m/s, 연속 추력 280 N, 추력 계수(K_m) 34.7 N/A를 가진다. 1 μm 분해능의 아날로그 사인 엔코더(Renishaw)를 측정에 사용한다.

Fig. 1

Control system of the RFC linear motor motion stage

2.2 전류 제어 알고리즘

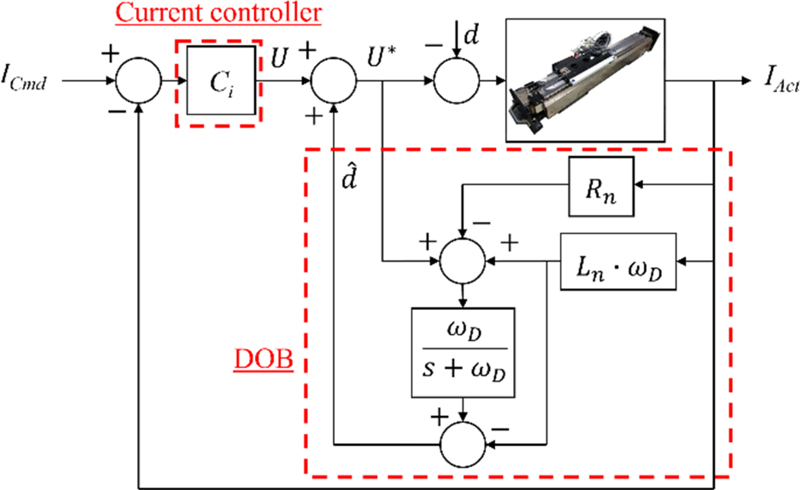
Power PMAC 제어기의 전류 제어 알고리즘은 Fig. 2와 같이 d/q축 PI 제어와 후진 경로 비례 이득(K_pb)을 포함한다. d축 전류 명령(I_dCmd)은 0이고, q축 전류 명령(I_qCmd)은 위치 제어 추력 명령이다. 각 제어기 출력은 식(1)과 같이 역 Park and Clarke 변환을 거쳐 3상으로 PWM 드라이버에 입력된다. 측정된 실제 3상 전류는 다시 식(2)와 같이 Park and Clarke 변환을 거쳐 d/q축 전류 제어기로 궤환된다. Power PMAC 전류 제어기를 분석해 동일한 구조를 갖는 전류 제어기 유저 코드를 C언어로 작성하여 구현하였다.

Fig. 2

Block diagram of PMAC current controller

2.3 전류 제어 실험

2.3.1 주파수 응답 비교

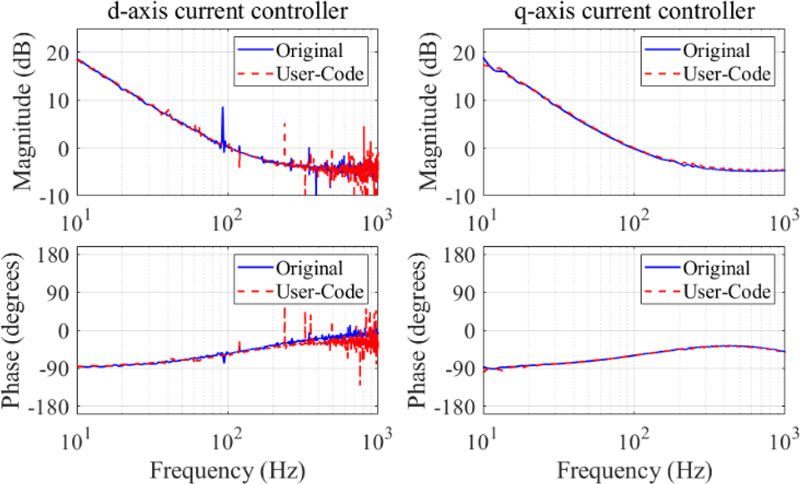
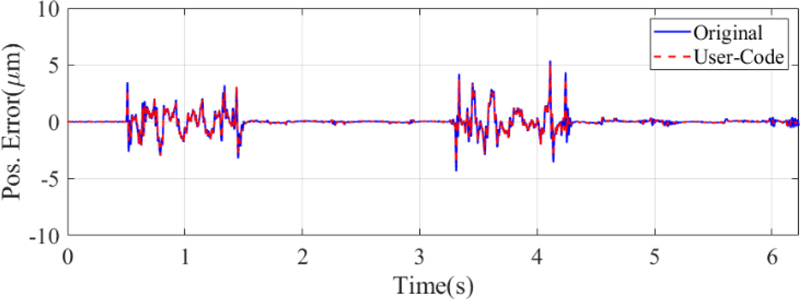
상용 제어기와 유저코드 전류 제어기 성능을 비교하기 위해 위치 제어기 서보 출력단에 1-1 kHz의 다중 주파수 정현파 신호를 주입하고 주파수 응답을 측정하여 Fig. 3에 나타냈다. 상용제어기와 유저 코드 전류 제어기는 동일한 주파수 응답을 가진다. d축 전류 명령과 제어 출력은 거의 0에 가깝기 때문에 전류 명령으로 충분한 가진이 어려워 측정 주파수 응답에 잡음이 포함되어 있다.

Fig. 3

FRF of current controllers

$\[ \left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]=\left[\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_p\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_p\right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_p+\frac{2}{3}\pi \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_p+\frac{2}{3}\pi \right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_p-\frac{2}{3}\pi \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_p-\frac{2}{3}\pi \right)\end{array}\right]\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right] \]$

(1)

$\[ \left[\begin{array}{c}{I}_d\\ I_q\end{array}\right]=\left[\begin{array}{c}cos\left({\theta }_p+\frac{\pi }{2}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}cos\left({\theta }_p+\frac{7\pi }{6}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\cos \left({\theta }_p-\frac{\pi }{6}\right)\\ sin\left({\theta }_p+\frac{\pi }{2}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}sin\left({\theta }_p+\frac{7\pi }{6}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\sin \left({\theta }_p-\frac{\pi }{6}\right)\end{array}\right]\left[\begin{array}{c}{I}_a\\ I_b\\ I_c\end{array}\right] \]$

(2)

2.3.2 시간 영역 성능 비교

Fig. 4와 같이 이동 거리 200 mm, 최대 속도 250 mm/s, 최대 가속도 2,500 mm/s²의 모션 프로파일에 대한 d/q축 전류 명령, 실제 전류, 그리고 전류 오차를 Fig. 5에 나타냈다. 그리고 각 제어기 위치 명령 추종오차를 Fig. 6에 나타냈다. 유저 코드로 구현된 전류 제어기 추종 성능이 기존 PowerPMAC 전류 제어기와 동일하였다.

Fig. 4

Motion profiles

Fig. 5

Current and current errors

Fig. 6

Position errors

2.4 전류 외란 관측기(DOB)

반발력 보상 선형 모터 모션 스테이지 고속 운전으로 발생하는 역기전력과 같은 외란을 보상하기 위해 d/q축 전류 제어기에 외란 관측기를 적용하였다. 전류 외란 관측기의 구조는 Fig. 7와 같고 공칭 인덕턴스(L_n), 공칭 저항(R_n), 절점주파수(ω_D)를 가지는 1차 Q 필터로 구성된다. 식(3)과 같이 선형 모터 실제 전류(I_ACT), 전류 제어기 출력(U^*) 그리고 1차 Q필터로 외란을 추정하여 보상할 수 있다.

Fig. 7

Block diagram of Current DOB

$\[ \begin{array}{c}\widehat{d}=\frac{{\omega }_D}{s+{\omega }_D}\left(U^{*}+L_n{\omega }_D{I}_{Act}+R_n{I}_{Act}\right)-L_n{\omega }_D{I}_{Act}\\ =\frac{{\omega }_D}{s+{\omega }_D}{U}^{*}+\left(-\frac{s}{s+{\omega }_D}{L}_n{\omega }_D{I}_{Act}-\frac{{\omega }_D}{s+{\omega }_D}{R}_n{I}_{Act}\right)\\ =\frac{{\omega }_D}{s+{\omega }_D}{U}^{*}-\frac{{\omega }_D}{s+{\omega }_D}{I}_{Act}\left(L_{n}s+R_n\right)\\ =\frac{{\omega }_D}{s+{\omega }_D}{U}^{*}-\frac{{\omega }_D}{s+{\omega }_D}\frac{U^{*}-d}{L_{n}s-R_n}\left(L_{n}s+R_n\right)=\frac{{\omega }_D}{s+{\omega }_D}d\end{array} \]$

(3)

3. 주파수 영역 전류 제어기 설계

3.1 주파수 응답 측정

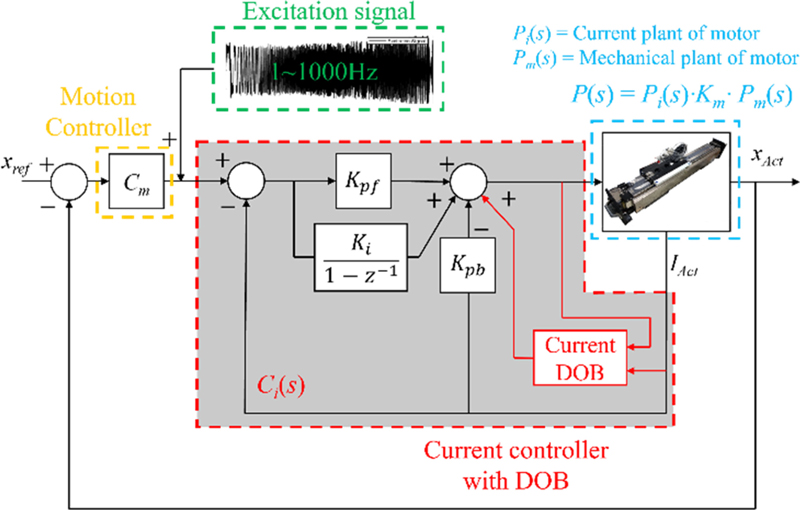
Fig. 8과 같이 1-1 kHz 다중 정현파 신호를 주입하여 전기 시스템(P_i)과 기계 시스템(P_m)을 포함한 선형 모터 모션 스테이지(P), 위치 제어(C_m) 그리고 전류 제어(C_i)로 구성된 전체 시스템 주파수 응답을 측정하였다. 가진 신호 주입 전후의 위치 제어기 출력을 이용하여 개루프 주파수 응답을 측정하였다.

Fig. 8

Schematic of frequency response measurement

3.2 주파수 응답 기반 전류 제어기 설계

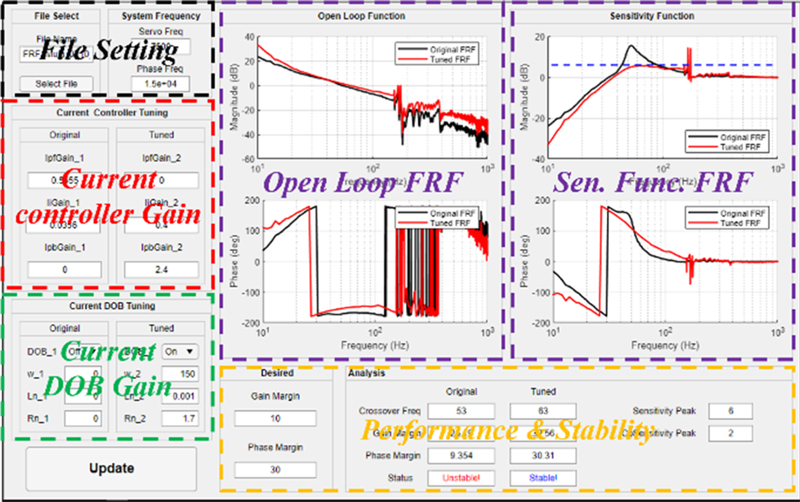
전류 제어가 포함된 모션 제어 시스템의 안정성과 성능을 예측하고 평가하기 위해 Fig. 9와 같은 주파수 응답 기반 전류 제어 튜닝 GUI를 개발하였다. 기존 전류 제어 이득, 외란 관측기가 포함된 전류 제어기 전달함수 식(4)와 3.1에서 측정한 개루프 전달함수 주파수 응답을 이용해 제어 이득 변화에 따른 개루프 전달함수, 폐루프 민감도 함수, 대역폭, 이득 및 위상 여유변화를 예측할 수 있다. 특히, Fig. 9 오른쪽 폐루프 민감도 함수에서 기계 모드에 의한 최댓값이 크기 때문에 전체 주파수 응답을 고려한 제어 이득 조절이 필요하다. Table 1에 튜닝 전후의 전류 제어기 이득을 표시하였다.

Fig. 9

Frequency response based Current control tuning GUI

Table 1

Current controller tuning

$\[ C_i\left(s\right)=\frac{K_{pf}+\frac{K_i}{s}}{\frac{s}{s+{\omega }_D}+P_i\left(s\right)\left[\left(L_{n}s+R_n\right)\frac{{\omega }_D}{s+{\omega }_D}+K_{pb}\right]} \]$

(4)

4. 실험 결과

4.1 주파수 영역 전류 제어기 설계 결과

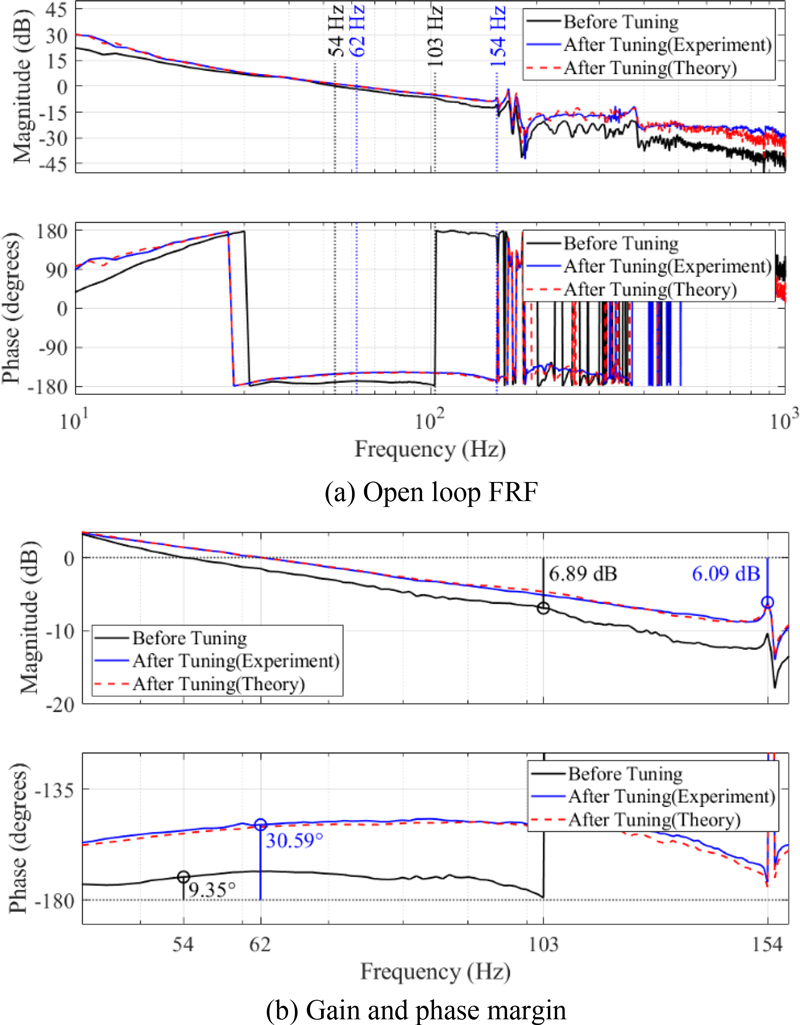
전류 제어 이득 조절 전후 이론 및 실험 개루프 전달 함수 주파수 응답을 Fig. 10에 나타냈다. 이득 조절 후 대역폭과 이득 및 위상 여유 변화를 각각 Figs. 10(a)와 10(b)에 나타냈다. 전류제어 튜닝 GUI 예측 정확도는 Table 2와 같이 대역폭이 99.87%, 위상 여유가 97.22%, 이득 여유가 98.92%이다.

Fig. 10

FRF of the open-loop transfer function

Table 2

Accuracy of the current control tuning GUI

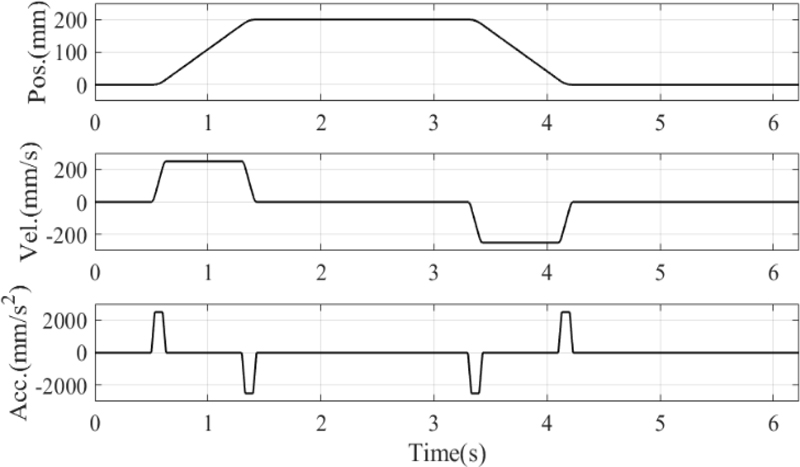
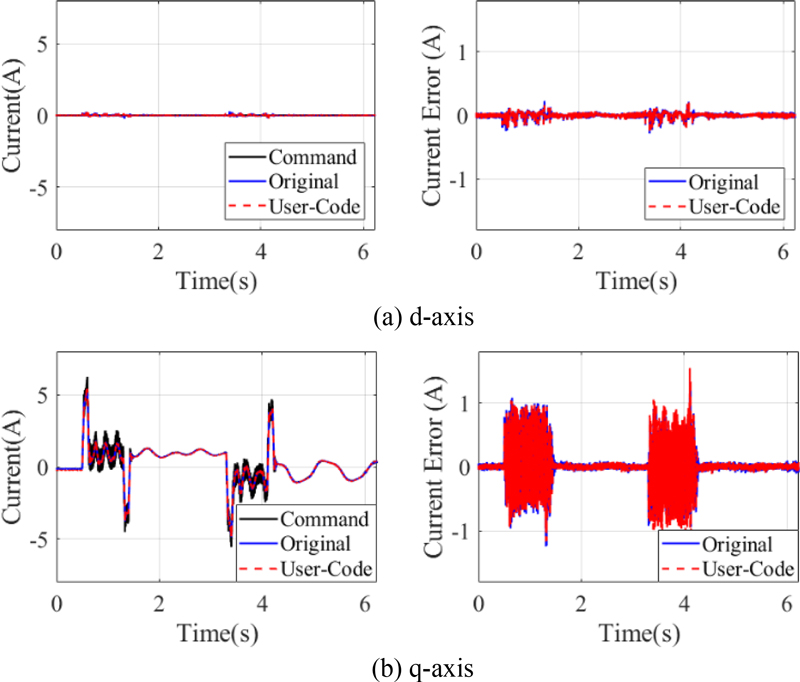
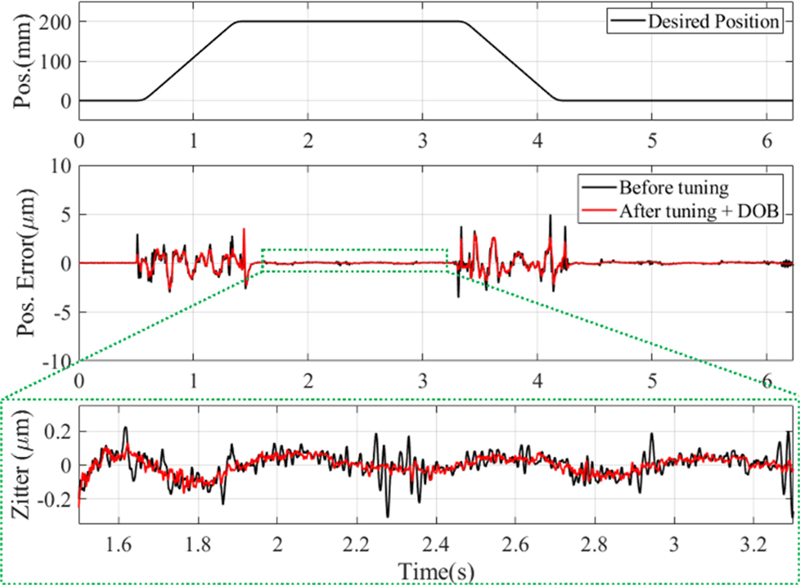
4.2 시간 영역 성능 평가

4.2.1 모션 스테이지 위치 결정 성능 평가

Fig. 4의 모션 프로파일을 사용하여 전류 제어 이득 조절 전후 모션 스테이지 위치 결정 성능, 즉, 추종 오차와 지터를 Fig. 11에 나타냈다. 동일한 위치 제어 이득에서 전류 제어 이득 조절만으로 지터의 평균 제곱근 오차가 12.19% 감소했다. 0.2 mm 저주파 지터는 반발력 보상 선형 모터 모션 스테이지의 자석 트랙 잔류 진동으로 발생하며 위치 제어 외란 관측기로 지터 크기가 크게 감소했지만 추가 보상을 위한 연구가 진행 중이다[11-12].

Fig. 11

Following errors

4.3 외란 제거 성능 평가

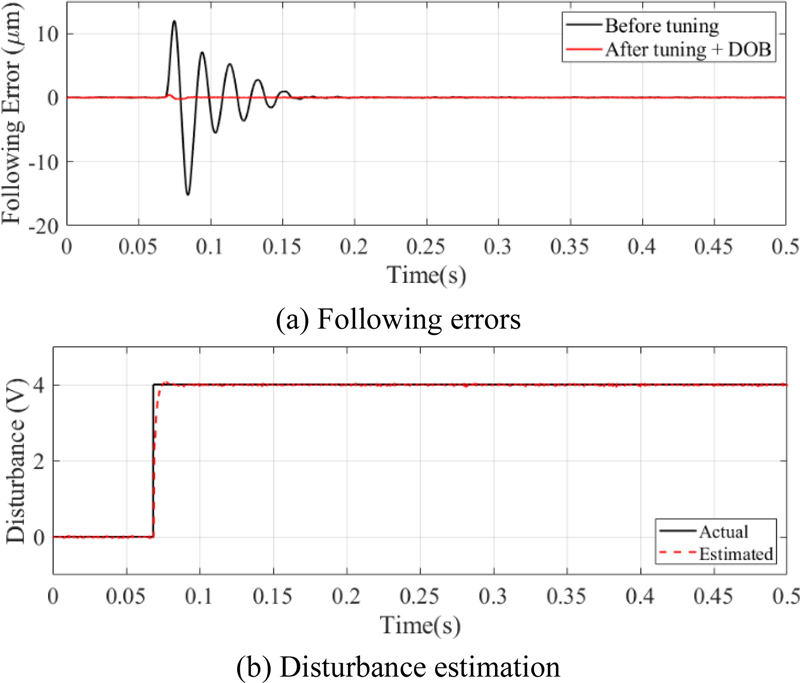
전류 외란 관측기의 외란 제거 성능을 평가하기 위해 크기 4 V 계단 외란을 d/q축 제어기 출력단에 입력하였다. 외란을 입력한 추종 오차를 Fig. 12(a)에, 입력한 외란과 추정 외란을 Fig. 12(b)에 나타내었다. 외란 관측기 적용후 전압 외란에 의한 추종 오차가 82.41% 감소했다.

Fig. 12

Current DOB experiment

5. 결론

이 연구에서는 반발력 보상 선형 모터 모션 스테이지의 위치 결정 성능을 향상시키기 위해 맞춤형 전류 제어 방법을 개발하고 이를 실험적으로 검증하였다. 먼저 상용 Power PMAC 모션 제어기의 전류 제어기와 동일한 구조를 갖는 유저 코드를 개발했다. 전류 외란 관측기가 포함된 전류 제어기 주파수 영역 설계를 위해 개루프 전달함수의 주파수 응답을 측정하여 전류 제어기 이득을 조절할 수 있는 전류 제어 튜닝 GUI를 개발하였다. 전류 제어 튜닝 GUI는 전류 제어 이득 조절 전후 대역폭을 99.87%, 위상 여유를 97.22%, 이득 여유를 98.92%의 정확도로 예측하였다. 주파수 영역 기반 전류 제어기 이득 조절 후 지터의 평균 제곱근 오차가 12.19% 감소했다. 전류 제어기 출력단 4 V계단 외란의 제거 성능을 비교한 결과 외란에 의한 추종 오차가 82.41% 감소하여 맞춤형 전류 제어기의 효과를 실험적으로 검증했다.

Acknowledgments

This paper was presented at KSPE Spring Conference in 2024

이 연구는 산업통상자원부(한국산업기술평가관리원) 산업기술혁신사업(2021년도 소재부품기술개발사업)의 지원으로 수행되었음(20017202).

REFERENCES

• Chen, Z., Yao, B., Wang, Q., (2014), μ-Synthesis-based adaptive robust control of linear motor driven stages with high-frequency dynamics: A case study, IEEE/ASME Transactions on Mechatronics, 20(3), 1482-1490. [https://doi.org/10.1109/TMECH.2014.2369454]
• Schmidt, R. H. M., (2012), Ultra-precision engineering in lithographic exposure equipment for the semiconductor industry, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 370(1973), 3950-3972. [https://doi.org/10.1098/rsta.2011.0054]
• Kim, Y. H, Kim, K.-S., Kim, S. H., (2015), A DOB based robust current control of Permanent Magnet Synchronous Motor, Proceedings of the 15th International Conference on Control, Automation and Systems (ICCAS), 301-306. [https://doi.org/10.1109/ICCAS.2015.7364927]
• Chen, H. C., Huang, M. S., Liaw, C. M., Chang, Y. C., Yu, P. Y., Huang, J. M., (2000), Robust current control for brushless DC motors, IEE Proceedings-Electric Power Applications, 147(6), 503-512. [https://doi.org/10.1049/ip-epa:20000629]
• Liu, J., Wu, W., Chung, H. S.-H., Blaabjerg, F., (2019), Disturbance observer-based adaptive current control with selflearning ability to improve the grid-injected current for LCLfiltered grid-connected inverter, IEEE Access, 7, 105376-105390. [https://doi.org/10.1109/ACCESS.2019.2931734]
• Wallscheid, O., Ngoumtsa, E. F. B., (2020), Investigation of disturbance observers for model predictive current control in electric drives, IEEE Transactions on Power Electronics, 35(12), 13563-13572. [https://doi.org/10.1109/TPEL.2020.2992784]
• Zhang, M.-G., Wang, X.-G., Liu, M.-Q., (2005), Adaptive PID control based on RBF neural network identification, Proceedings of the 17th IEEE International Conference on Tools with Artificial Intelligence (ICTAI'05), 681-683.
• Chen, Y., Yang, M., Long, J., Qu, W., Xu, D., Blaabjerg, F., (2019), A moderate online servo controller parameter self-tuning method via variable-period inertia identification, IEEE Transactions on Power Electronics, 34(12), 12165-12180. [https://doi.org/10.1109/TPEL.2019.2909439]
• Malassé, O., Zasadzinski, M., Razik, H., Iung, C., (1993), A comparison of robust loop shaping designs: an application to an electromechanical actuator, Proceedings of IEEE Systems Man and Cybernetics Conference-SMC, 3(1), 764-769. [https://doi.org/10.1109/ICSMC.1993.385110]
• Nguyen, D. C., Ahn, H. J., (2014), Dynamic analysis and iterative design of a passive reaction force compensation device for a linear motor motion stage, International Journal of Precision Engineering and Manufacturing, 15, 2367-2373 [https://doi.org/10.1007/s12541-014-0602-8]
• Yoo, S. J., Ahn, H.-J., (2020), Software-based integral product architecture for modular motion control system of a RFC linear motor motion stage: Model-based DOB for residual vibration suppression, International Journal of Precision Engineering and Manufacturing, 21, 203-209. [https://doi.org/10.1007/s12541-019-00212-y]
• Jeon, H. W., Ahn, H. J., (2024), Model-based motion control design of a linear motor stage in frequency domain, Journal of the Korean Society for Precision Engineering, 41(1), 55-60. [https://doi.org/10.7736/JKSPE.023.107]