건설자재의 반복적 층간 이송을 위한 리프팅 장치와 단일 스프링을 이용한 기계적 중력 보상 방안

1. 서론

업무강도가 높은 현장을 대표하는 건설현장에서도, 작업자들은 다양한 작업들 중 육체적으로 가장 힘든 작업으로 형틀작업을 꼽는다[1]. 콘크리트 건축물 시공에 내·외벽의 콘크리트 타설을 위한 거푸집이 사용되는데, 이 거푸집을 설치 및 해체하는 작업이 바로 형틀작업이다. 형틀작업은 거푸집 패널을 포함한 무거운 자재들을 위층으로 운반하는 작업을 포함하고 있어, 작업자들에게 가장 부담스러운 작업으로 여겨진다. 거푸집은 과거에 목재로 구성되었으나, 고 하중의 지지와 재사용의 목적으로 최근에는 금속 재료로 대체되고 있다. 이로 인해 대형 구조물 건설의 소요시간 및 비용을 크게 줄일 수 있게 되었지만, 단일 거푸집 패널의 크기와 무게는 오히려 증가하였다[2]. 현재 주로 사용되는 알루미늄 거푸집 패널(Aluminum-formwork, 알폼)의 경우 그 무게가 최대 30 kg에 달한다. 이와 같은 무겁고 많은 자재들을 직접 들어 올려 위층으로 운반하는 고중량, 고반복 작업은 작업자들의 근골격계 질환을 악화시키고 있다[3,4]. 이를 개선하기 위해 자재의 경량화에 대한 연구가 지속되고 있지만[5], 작업자가 느끼는 작업 강도를 극적으로 완화시키기에는 한계가 있다.

건설 자재 이송의 높은 작업 강도를 감소시키기 위하여, 작업을 부분적으로 자동화하려는 시도가 이루어지고 있다. 일례로, 층간 이송 작업의 도달거리와 작업자의 낭비되는 동작을 줄일 수 있는 테이블 리프트가 도입되어, 관절 부하의 감소 및 생산성의 증가를 위한 일부 역할을 하고 있다[6]. 그러나 테이블 리프트는 자재를 위층으로 들어 올릴 때 일부 개선을 제공하지만, 위층에서 받아주는 작업자에게는 도움을 주지 못한다. 몇몇 현장에서는 거푸집 패널을 위층으로 이송하기 위한 패널 전용 인양기가 도입되고 있다[7]. 그러나 이러한 전용 인양기는 롤러가 주요 메커니즘으로 적용되었기 때문에 패널의 이송에만 사용될 수 있으며, 다양한 형태의 자재 운반에는 적합하지 않다는 한계가 있다.

한편, 건설작업을 자율화하여 현장 인력을 완전히 배제하기 위한 장기적인 차원에서의 노력도 꾸준하게 이루어지고 있다. AGV (Automated Guided Vehicle, 무인 운반차량)와 모바일 매니퓰레이터 등을 활용하여 다양한 작업을 대체하기 위한 연구가 진행되고 있고[8-10], Near-site Robotic Platform과 3D프린팅 기술을 활용한 OSC (Off-Site Construction, 탈 현장 건설)에 대한 연구들도 이루어지고 있다[11-13]. 그러나 이러한 시도들이 아직은 연구 차원에 머물러 있으며, 현장 환경의 다양성 및 작업의 가변성으로 인해 건설 현장의 인력 투입은 여전히 필수적이다. 따라서 작업의 완전 자율화보다는 특정 강도 높은 작업을 도와줄 수 있는 로봇의 도입이 필요하다.

본 논문에서는 건설현장에서 형틀 작업 중 발생하는 거푸집 패널 층간 이송작업의 작업강도를 크게 완화시키기 위하여, 건설자재의 반복적인 층간 이송 작업을 수행하는 리프팅 장치를 제안한다. 이 장치는 기어로 구속된 이중 평행 4절 링크가 기반이 되어 1-자유도 수직운동을 하며, 말단링크가 지면과의 수평을 유지한다. 그뿐만 아니라, 이 장치의 안정성을 위하여 구조적 특성 및 작업의 한 사이클이 고려된 적정 중력 보상 적용방법 또한 제시한다. 따라서 이어지는 논문의 2장에서는 장치의 구조적인 구성을 설명하고, 3장에서는 적용된 중력 보상에 대한 기구학적 해석을 설명한다. 그리고 4장에서는 제안한 장치의 효용성을 확인하기 위한 시제품의 제작 및 실험을 수행한다. 실험결과에 대한 분석 및 논의가 5장에서 이어지며, 마지막으로 6장에서 결론에 대해 정리하며 논문이 마무리된다.

2. 리프팅 장치의 기구적 구조

일반적으로 물체의 이송 작업에는 픽앤플레이스(Pick-andplace)를 위한 매니퓰레이터와 운송을 위한 모바일로봇이 활용 될 수 있다[14]. 그러나 단순히 물체를 위층으로 옮기는 작업에 있어서, 이러한 로봇들의 활용은 정밀한 제어에 막대한 비용이 발생할 뿐만 아니라, 에너지 효율이 크게 떨어지게 된다. 에너지 효율을 고려한다면, 층간의 가장 짧은 거리인 수직경로를 따라 자재를 이송하는 것이 바람직하다. 따라서 해당 수직경로를 반복 운동할 수 있는 특별한 기구적 설계가 필요하다.

2.1 기어로 구속된 두 개의 평행 4절 링크

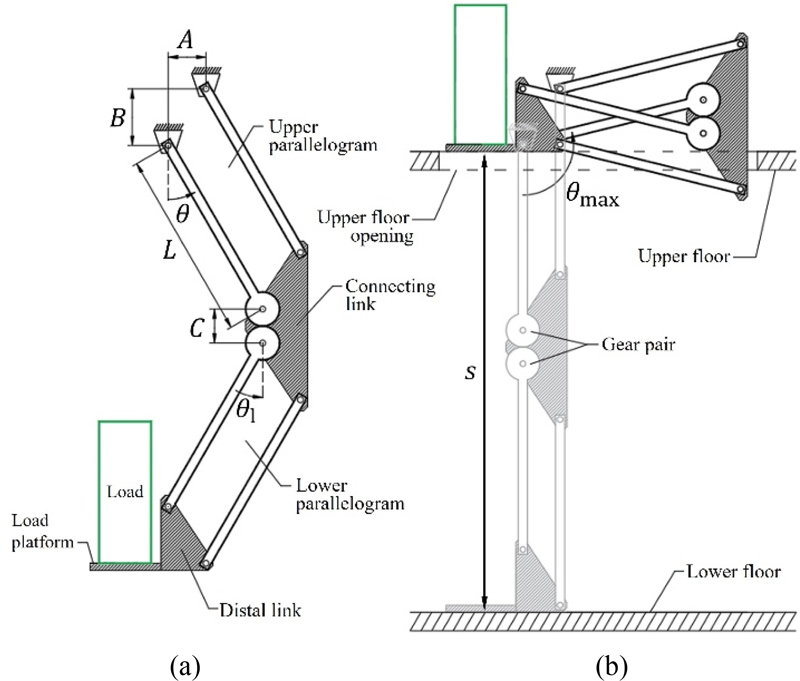
평행 4절 링크(Parallelogram Mechanism)는 4개의 링크로 구성된 메커니즘으로, 일정한 각도에서 링크들이 서로 평행하게 움직이는 구조를 의미한다. 제안하는 리프팅 장치는 이러한 구조를 활용해 Fig. 1과 같이 말단링크에 위치한 자재 적재부가 지면과 수평이 유지될 수 있다. 이와 동시에 1-자유도 수직 운동이 가능하도록, 동일한 평행 4절 링크 두 개가 연결 링크를 통하여 한 쌍의 기어로 구속된다. 그리고 적재부가 자재 인양용 개구부를 안정적으로 통과할 수 있도록, 베이스는 상층에 위치 되어 아래층의 자재를 위층으로 받아 올릴 수 있는 구조로 설계된다. Fig. 1(b)와 같이 기구의 초기자세(θ = 0°)에서 적재부가 하층에 위치하며, 구동 목표 지점(θ = θ_max)에서는 적재부가 상층부의 베이스에 위치하게 된다. 최종 구동 각 θ_max와 적재부의 이동 거리 s는 회전 링크의 길이 L, 평행 4절 링크의 길이방향 오프셋 B 그리고 기어 사이의 거리 C에 의해 다음과 같이 결정된다.

Fig. 1

Some postures of proposed double parallelogram: (a) θ=30° and (b) θ=θmax

$\[ {\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}={\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left(-\frac{B+C}{2L}\right) \]$

(1)

$\[ s=2L+B+C \]$

(2)

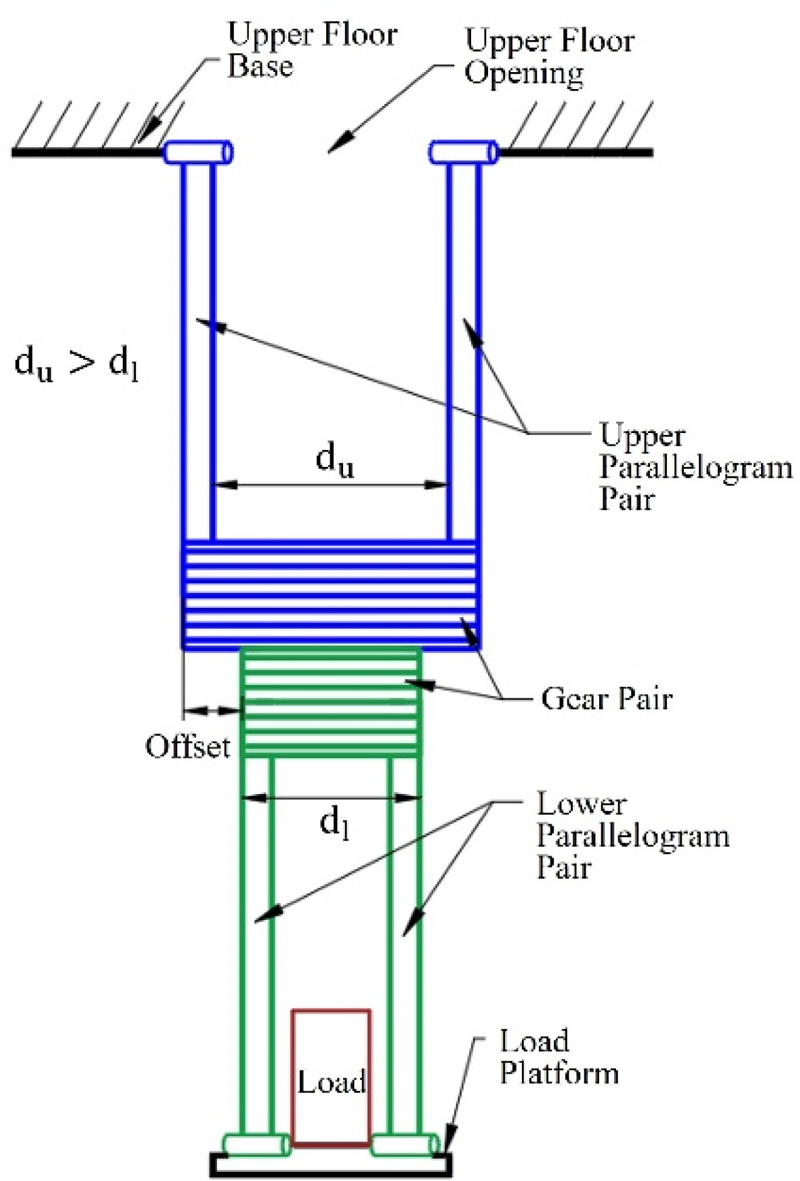
한편, 적재부가 목표 지점까지 도달하기 위하여 두 개의 평행 4절 링크는 서로 겹쳐지는 범위에서도 충돌 없이 구동될 수 있어야 한다. 이때 위쪽 평행 4절 링크의 운동 평면과 아래쪽 평행 4절 링크의 운동 평면 사이에 오프셋이 적용되면 부품 간의 충돌을 방지할 수 있다. 따라서, Fig. 2에 도시된 바와 같이 위쪽 평행 4절 링크 쌍의 폭 d_u보다 아래쪽 평행 4절 링크 쌍의 폭 d₁이 작도록 설계되는 것이 바람직하다.

Fig. 2

Arrangement of parallelograms in side-view

Fig. 3는 단순화된 이중 평행 4절 링크의 정역학 모델을 나타낸다. 여기서 평행 4절 링크를 구성하는 두 개의 회전 링크는 하나의 링크로 도시되고, 무게중심의 위치는 링크의 중앙으로 가정된다. 이때 기구의 자세를 정적으로 유지시키기 위하여 기어 관절 J₁을 통해 전달받아야 하는 토크 M_1,g는 다음과 같다.

Fig. 3

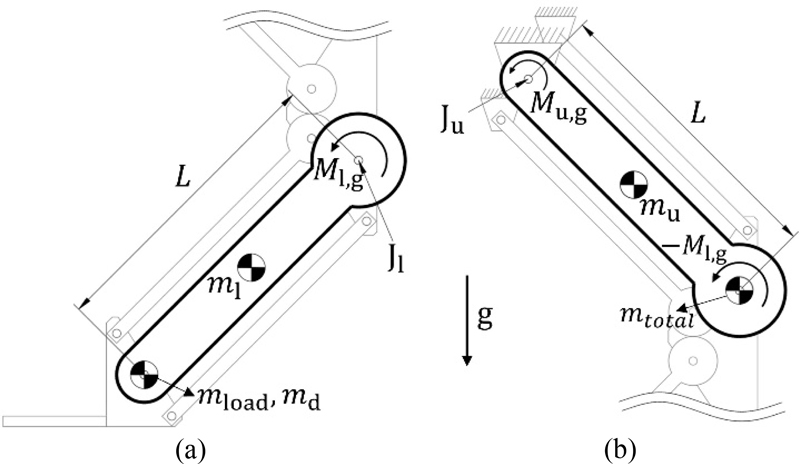
Simplified torque diagram of each parallelogram: (a) Lower parallelogram and (b) Upper parallelogram

$\[ M_{1,\mathrm{g}}=-\left(m_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d} }+m_{\mathrm{d}}+\frac{1}{2}{m}_1\right)gL\mathrm{s}\mathrm{i}\mathrm{n}\theta \]$

(3)

여기서 m_load와 m_d는 각각 자재와 말단링크의 무게이고, 무게중심은 말단링크의 위에 있다고 가정한다. 또한 m₁은 아래쪽 평행 4절 링크를 구성하는 회전 링크 두 개의 무게를 의미한다. 이 토크 M_1,g는 기어를 통해 위쪽 평행 4절 링크로부터 전달되어야 한다. 따라서 Fig. 3(b)의 위쪽 평행 4절 링크에서, 정적 평형을 위하여 베이스 관절 J_u에서 필요한 토크 M_u,g를 다음과 같이 계산할 수 있다.

$\[ M_{\mathrm{u},\mathrm{g}}=\left(m_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}+\frac{1}{2}{m}_{\mathrm{u}}\right)gL\mathrm{s}\mathrm{i}\mathrm{n}\theta -M_{1,\mathrm{g}} \]$

(4)

여기서 m_total = m_load + m_d + m₁ + m_c이고, m_c는 중간의 연결링크 무게, m_u는 위쪽 평행 4절 링크를 구성한 회전 링크 두 개의 무게를 의미한다. 이때 m_total의 무게중심은 기어 관절 위에 있다고 가정한다.

2.2 구동을 위한 크랭크-로커

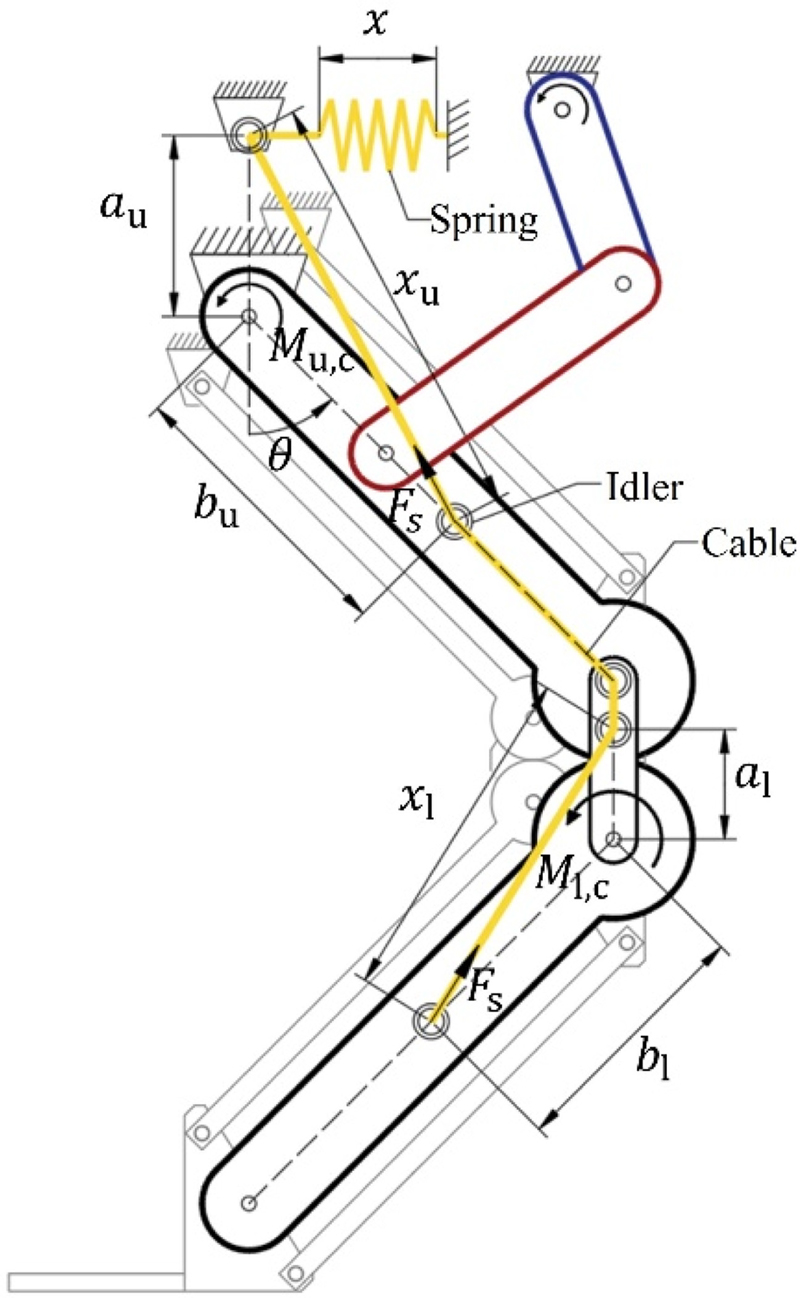
제안하는 리프팅 장치의 현장 적용 가능성을 높이기 위해서는 많은 자재를 신속하게 반복 이송할 수 있어야 한다. 그러나 이중 평행 4절 링크를 베이스 관절에서 직접 구동하기 위해서는 구동기에 상당한 토크가 필요하며, 정확한 포지셔닝을 위한 제어의 문제도 따른다. 따라서 Fig. 4(a)에서 보이는 대로 위쪽 평행 4절 링크의 회전 링크에 구동을 위한 파란색 크랭크와 빨간색 커플러 링크를 추가로 적용한다. 결과적으로 반복 작업에 유리하고, 구동 시 필요한 최대 토크가 작으며, 정확한 제어의 부담을 줄일 수 있는 크랭크-로커 메커니즘이 구성될 수 있다. 이를 구성하는 크랭크, 커플러, 로커와 베이스 링크의 길이 l_cr, l_cp, l_r와 l_b는 Grashof Condition을 만족하는 값 중에서 선택될 수 있다. 크랭크-로커는 두 개의 특이점을 가지므로, 각 특이점에서 로커의 각도가 θ = 0°와 θ = θ_max를 만족시키는 링크의 길이가 기구학적 관계로부터 선택될 수 있다. 그 결과로 크랭크가 반시계 방향으로 등속 회전할 때, 적재부는 최고점과 최저점 사이를 반복적으로 왕복운동 하게 되고, 두 지점에서 순간속도는 0이 된다. 한편, 본 연구에서는 크랭크가 회전한 각이 φ = 0°와 φ = 180°일 때 크랭크-로커가 특이점이 되도록 설계하여, 적재부의 상승과 하강에 소요되는 시간이 동일하다. 결과적으로 φ = 0°와 φ = 180°에서 각각 θ = 0°와 θ = θ_max를 만족한다. 이때 기구의 자세유지를 위하여 구동 관절 J_c에서 필요한 토크 M_c는 Fig. 4(b)의 4절 링크에서 관절 간의 관계로부터 다음과 같이 계산될 수 있다.

Fig. 4

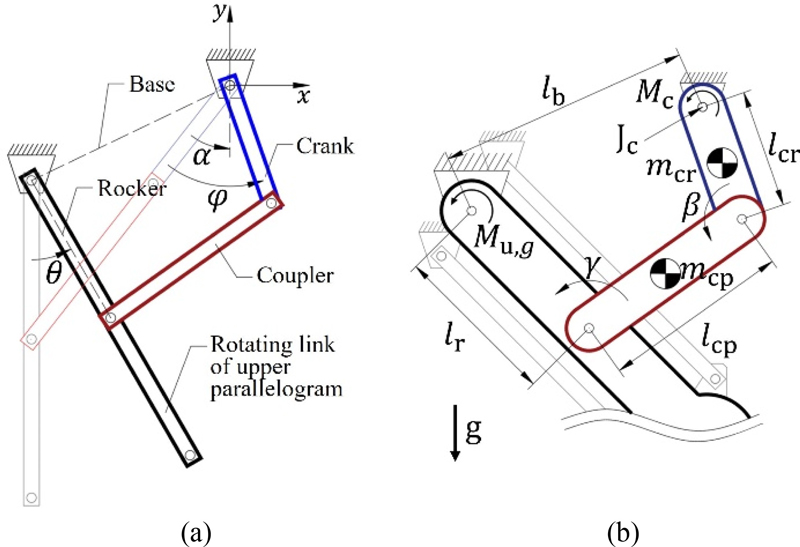
Applied crank-rocker mechanism to drive double parallelogram: (a) Attached links and (b) Components diagram

$\[ M_c=\frac{l_{\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\gamma }{l_{\mathrm{c}\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\beta }{M}_{\mathrm{u},\mathrm{g}}-\left(m_{\mathrm{c}\mathrm{p}}+\frac{1}{2}{m}_{\mathrm{c}\mathrm{r}}\right)g{l}_{\mathrm{c}\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha -\phi \right) \]$

(5)

여기서 첫 번째 항은 M_u,g에 의해 J_c에 전달되는 토크이고, 두번째 항은 크랭크와 커플러 링크의 무게 m_cr, m_cp에 의한 토크를 의미한다. γ와 β는 각각 로커와 커플러 링크, 커플러와 크랭크 링크가 이루는 각을 뜻하며, α는 θ = 0°인 초기 자세일 때 크랭크 링크가 y축과 이루는 각이다.

3. 중력 보상의 적용과 구동 시뮬레이션

현장 적용 가능성을 높이기 위해서는 장치의 비용 또한 중요하다. 그뿐만 아니라 현장의 작업자에게 위험을 최소화하는 동시에 실제 작업 성능에도 부족함이 없으며, 기계적으로 높은 강성을 가져야 한다. 그러나 장치에 사용되는 고용량의 구동기는 가장 직접적으로 가격에 영향을 주고, 충돌이나 끼임 등의 상황에서 작업자들의 안전에 위협이 될 수 있다. 따라서 기구의 자중과 적재하중에 의한 토크를 적절히 보상하여 구동기의 용량을 낮추고, 장치의 안전성을 향상시키는 것이 필요하다.

3.1 스프링과 케이블을 이용한 기계적 중력 보상

일반적으로 다관절 로봇의 중력 토크를 보상할 때는 관절마다 별도의 스프링을 사용한다[15]. 이러한 스프링들은 보통 로봇의 내부에 배치되며, 중력에 의한 토크를 상쇄시킨다. 하지만 이 경우, 로봇의 자중이 증가하게 되며, 설계에 공간적인 제약이 추가로 발생하게 된다.

한편, 제안된 장치는 기어로 구속된 1-자유도 구조를 가지고 있어, 위쪽 링크만 구동하더라도 원활히 동작해야 한다. 하지만 자재를 이송하는 적재부가 아래쪽 평행 4절 링크의 하단에 위치하여, 무거운 자재를 적재할 경우 기어 관절에 큰 토크가 발생하게 된다. 이로 인해, 아래쪽 평행 4절 링크는 구조적으로 안정성이 낮아지며, 실제 구동에서는 부품 사이의 유격과 부품의 변형 등에 의하여 적재부 포지셔닝 오차가 발생할 수 있다. 따라서 기구의 정역학 모델링 상 J_u와 J_l 두 관절의 토크를 모두 보상하는 것이 바람직하다. 이를 위해 하나의 스프링을 사용하여 두 관절의 중력 토크를 모두 보상하는 특별한 방법을 적용하면, 장치의 성능을 유지하면서도 공간 효율성과 구조적 안정성을 높일 수 있다.

우선, 스프링이 베이스 부근, 장치의 외부에 고정된다. 스프링은 케이블로 연장되고, Fig. 5에서 노란색으로 도시된 케이블 루팅을 통하여 위아래 평행 4절 링크 모두에 스프링의 장력이 전달된다. 스프링은 장치의 자세 변화에 따라 변하며, 하나의 스프링이 두 개의 평행 4절 링크에 의해 인장되므로, 스프링에 더 큰 탄성에너지가 저장될 수 있다. 또한 스프링이 기구 내부에 있지 않으므로, 장치를 개구부 사이로 동작할 수 있는 좁은 폭을 가지도록 설계하기 유리하다.

Fig. 5

Simplified force diagram of cable tension

각 관절에 적절한 보상 토크를 적용하려면, 우선 스프링의 인장길이를 계산하는 것이 필요하다. 스프링의 아래쪽 평행 4절 링크에 의한 인장 길이 ∆x₁과 위쪽 평행 4절 링크에 의한 인장 길이 ∆x_u는 아이들러의 위치 a₁, b₁, a_u, b_u와 그 사이의 거리 x₁, x_u에 의해 다음과 같이 계산되며, 여기서 아이들러의 크기는 무시될 수 있다.

$\[ \Delta x_1=x_1-\left|a_1-b_1\right| \]$

(6)

$\[ \mathrm{\Delta }{x}_{\mathrm{u}}=x_{\mathrm{u}}-\left|a_{\mathrm{u}}-b_{\mathrm{u}}\right| \]$

(7)

따라서 스프링의 총 인장길이 x는 초기 인장 x₀가 포함되어 다음과 같이 계산된다.

$\[ x=x_0+\mathrm{\Delta }{x}_1+\mathrm{\Delta }{x}_{\mathrm{u}} \]$

(8)

다음으로는 계산된 스프링의 인장길이를 통해 스프링의 장력과 그로 인해 각 관절에 적용되는 보상 토크를 계산한다. 이때 스프링 장력 F_s는 스프링 상수 k에 의해 다음과 같이 계산된다.

$\[ F_s=kx \]$

(9)

이로부터 J_l에 발생하는 보상 토크 M_1,c가 a₁과 b₁에 의해 결정되며 다음과 같이 표현될 수 있다.

$\[ M_{1,\mathrm{c}}=-F_{\mathrm{s}}\frac{a_1{b}_1}{x_1}\mathrm{s}\mathrm{i}\mathrm{n}\theta \]$

(10)

반면, J_u에 발생하는 보상 토크 M_u,c는 a_u와 b_u에 영향을 받으며 다음과 같이 표현될 수 있다.

$\[ M_{\mathrm{u}.\mathrm{c}}=F_{\mathrm{s}}\frac{a_{\mathrm{u}}{b}_{\mathrm{u}}}{x_{\mathrm{u}}}\mathrm{s}\mathrm{i}\mathrm{n}\theta \]$

(11)

따라서 기구의 정적 평형을 위하여 J_l에서 기어로부터 전달받아야 하는 토크 M_l은 다음과 같이 계산된다.

$\[ M_1=M_{1,\mathrm{g}}-M_{\mathrm{l},\mathrm{c}} \]$

(12)

최종적으로 기구의 자세 유지를 위하여 J_u에서 필요한 토크 M_u는 다음과 같이 계산되고, 이를 식(5)의 M_u,g 대신 대입하여 구동기에서 필요한 토크 Mc를 구할 수 있다.

$\[ M_{\mathrm{u}}=M_{\mathrm{u},\mathrm{g}}-M_{\mathrm{u},\mathrm{c}}+M_{1,\mathrm{c}} \]$

(13)

구동 관절의 중력 토크를 완전히 보상하고자 한다면, 스프링 상수 k는 M_u= 0를 기준으로 결정될 수 있다. 그러나 실제 작업사이클에서는 자재를 싣고 상승 후 빈 적재부로 하강하기 때문에 하중의 변화가 발생한다. 따라서 적재 하중의 변화가 고려된 보상 토크가 특별히 선정될 필요가 있다. 이때 필요한 최대 구동 토크를 최소화한다면, 구동기 용량 또한 최소화하는 장점을 가질 수 있다. 최대 구동 토크는 상승 및 하강 시의 max(|M_u|) 값이 동일할 때 최소화되므로 구동기 용량을 최소화하는 최적의 스프링 상수 k는 적재할 하중 m_load을 고려하여, 다음 수식을 만족하는 값으로 결정될 수 있다.

$\[ k=\frac{\left(2m_{\text{load }}+4m_{\mathrm{d}}+3m_1+2m_{\mathrm{c}}+m_{\mathrm{u}}\right)gL}{2x\left(\frac{a_{\mathrm{u}}{b}_{\mathrm{u}}}{x_{\mathrm{u}}}+\frac{a_1{b}_1}{x_1}\right)} \]$

(14)

이때, 임의의 양수 c에 대해 a_u= ca₁과 b_u= cb₁의 조건을 가지고, 스프링의 초기 인장을 x₀ = |a_l – b_l| + |a_u – b_u| 로 설정하면, 다음과 같이 k가 유일해를 가질 수 있다.

$\[ k=\frac{\left(2m_{\text{load }}+4m_{\mathrm{d}}+3m_1+2m_{\mathrm{c}}+m_{\mathrm{u}}\right)gL}{2{\left(\mathrm{c}+1\right)}^2{a}_1{b}_1} \]$

(15)

3.2 구동 사이클 및 중력 보상 시뮬레이션

본 연구에서 제안하는 기구설계를 검증하기 위하여, 스케일 다운 모델이 제작되었다. 우선, 평행 4절 링크는 다음과 같은 길이로 구성되었다: A = 40, B = 60, L = 200 mm. 두 평행 4절 링크를 연결하는 기어는 모듈 2 mm와 잇수 18개로 구성되었으며, 이에 따라 C = 36 mm이다. 따라서 식(1)과 식(2)에 의하여, θ_max=103.89°, s=496 mm가 된다. 평행 4절 링크를 구성하는 회전 링크의 무게는 m_u = 0.75 kg와 m_l = 0.31 kg이며, 연결링크의 무게는 m_c = 0.33 kg이고, 말단 링크 및 적재부의 무게는 m_d = 0.21 kg으로 추후 제작을 고려하여 설정되었다. 그리고 각 링크의 무게 중심은 중앙으로 가정되었다.

크랭크-로커를 구성하는 4절링크는 φ = 0°와 φ = 180°에서 특이점 자세가 되며, 이때 로커의 각도는 θ = 0°와 φ = 103.89°를 만족한다. 우선, 로커 링크의 길이를 l_r= 100 mm로 설정한 후, 위 조건을 만족하며, 자세가 변하는 동안 링크간 간섭이 방지될 수 있는 J_c의 위치가 결정되었다. 이때 베이스의 길이는 l_b = 209.90 mm이다. 이에 따라, 크랭크와 커플러 링크 길이가 기구적 관계에 의해 각각 l_cr = 78.74 mm와 l_cp = 200.65 mm로 결정되었고, m_cr = 0.150 kg, m_cp = 0.072 kg으로 설정되었다.

한편, 다루고자 하는 자재의 무게는 m_load = 1.29 kg으로 설정되었고, 아이들러의 위치는 a₁ = a_u= 60 mm와 b₁ = b_u = 100 mm로 설정되었다. 따라서 스프링은 유일해를 위하여 초기인장 80 mm가 적용되었고, 식(15)에 의해 적절한 스프링상수는 k = 235 N/m로 결정되었다. Zero-free-length (ZFL)로 가정된 이 스프링은 식(8)에 의하여 장치의 구동 과정에서 θ = 103.89°일때 207.1 mm에서 θ = 0°일 때 320 mm까지 인장된다.

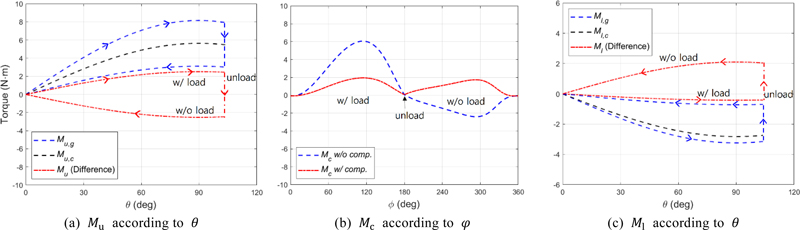
Fig. 6는 위의 설계 변수들이 적용된 M_u, M_c와 M_l을 한 사이클의 자세 변화에 대해 나타낸 것이다. Fig. 6(a)에서 확인할 수 있는 중력 보상이 적용된 M_u는, 목표한 바와 같이, 필요한 최대 토크가 상승 하강 동작에서 동일하도록 바뀌었다. 이에 따라, 크랭크 구동에 필요한 토크인 M_c의 최댓값이 Fig. 6(b)에서 나타난 것처럼 3분의 1로 줄어드는 것이 확인된다. 추가적으로, Fig. 6(c)에서 볼 수 있는 것처럼 중력 보상을 적용하게 되면 기어를 통해 전달되는 최대 토크를 감소시킬 수 있다.

Fig. 6

Results of gravity compensation simulation of each joint: (a) Ju, (b) Jc,and (c) Jl

4. 시제품 제작 및 실험

4.1 시제품 제작

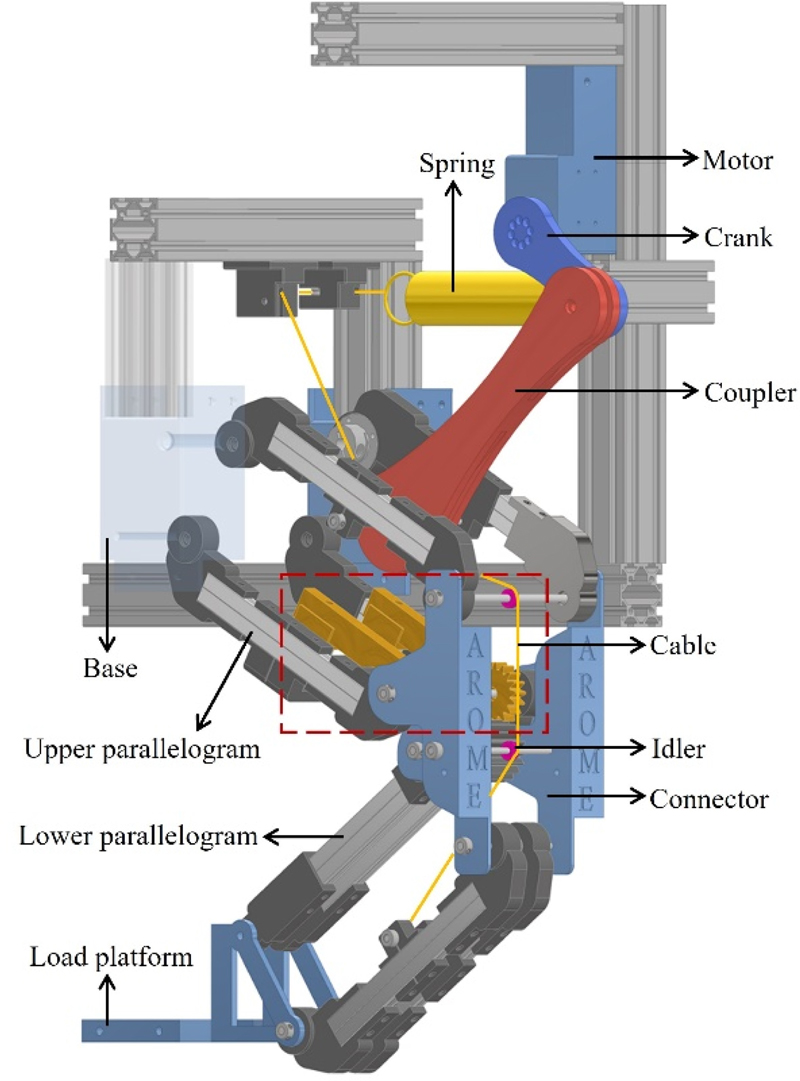
제안한 장치의 성능을 확인하기 위하여, Fig. 7과 같이 앞선 시뮬레이션과 동일한 설계변수를 가지는 시제품을 제작하고 구동 실험을 수행하였다. 2장에서 설명한 것처럼, 위쪽 평행 4절 링크 쌍의 폭이 아래쪽 평행 4절 링크 쌍의 폭보다 넓어 부품간 간섭 없이 구동될 수 있다. 시제품에 사용된 스프링의 강성은 235 N/m, 자유길이는 191.10 mm 그리고 초기장력은 15.034 N이다. 따라서 θ = 103.89°일 때 스프링에 143.13 mm의 초기인장을 주면, 유일해의 조건과 ZFL스프링의 특성을 가질 수 있다. 결과적으로 θ = 0° 일 때 스프링의 길이는 447.13 mm까지 인장된다. 이 스프링을 연장하는 케이블은 경로의 최대 길이인 a_u + L + 2B + C + b_l = 516 mm가 고려되어, 530 mm로 사용되었다. 이에 따라 스프링은 첫 번째 아이들러로부터 461.13 mm 떨어진 지점에 고정되었다. 이때 아이들러의 직경은 12 mm로 충분히 작아 그 크기를 무시할 수 있다.

Fig. 7

3D model of proposed lifting robot prototype

시제품의 제작에서 평행 4절 링크를 구성하는 회전 링크들은 20 × 10사이즈의 알루미늄 프레임을 골격으로 제작되었다. 연결부와 기어 등 비표준 부품들은 3D 프린팅을 활용하여 PLA소재로 제작되었다. SUS304 재질의 케이블은 7 × 19의 구성에 지름이 1 mm인 제품이 사용되었다. 그 외 베어링, 아이들러, 회전축 등 표준 부품들은 MISUMI사의 제품이 사용되었다. 장치의 구동을 위한 모터는 로보티즈 사의 XH540-W270-R (Nominal Voltage: 12 V, Stall Torque: 9.9 Nm)모델이 사용되었다.

4.2 구동 관절 토크 측정

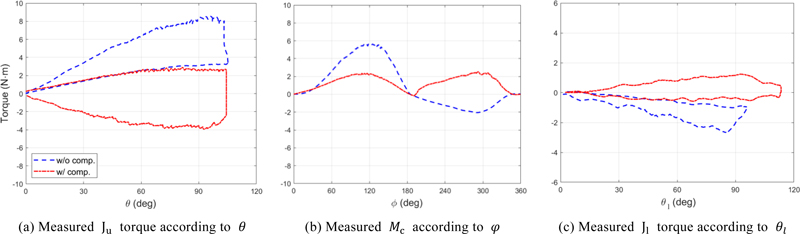
시제품이 제작된 후, 실제 구동하며 리프팅 장치의 유효성 검증을 위한 실험들을 진행하였다. 모든 실험은 각각 중력 보상 적용 전후로 수행되어 비교할 수 있도록 하였다. 우선, 중력 보상 적용의 효과와 시뮬레이션의 유효성을 검증하기 위하여 구동에 필요한 토크가 측정되었다. 이를 위해 Fig. 8과 같이 관절과 모터 사이에 봉신로드셀 사의 회전형 토크센서 BRDM-N10(Rated Capacity: 10 Nm)이 부착되었다. 먼저, 관절 J_u에 모터와 토크센서를 부착하여, 장치를 베이스 관절에서 직접 구동할 때 필요한 토크를 확인하였다. 하중 1.29 kg을 싣고 모터를 θ = 0°에서 θ = 103.89°까지 회전시킨 후, 하중을 제거하고θ = 103.89°에서 θ = 0°까지 한 사이클을 동작시켰다. 모터는 2 RPM의 느린 속도로 구동되었으므로, 준정적 과정으로 간주할 수 있으며, 그 결과는 Fig. 10(a)와 같다.

Fig. 8

Load lifting test of robot prototype

Fig. 9

Detail of gear connected part of the robot prototype (Red box in Fig. 7)

다음으로는 크랭크-로커 적용 시 장치의 구동에 필요한 토크를 측정하기 위하여, 크랭크 구동 관절 J_c에 모터와 토크센서를 부착하였다. 위와 동일한 하중을 싣고 모터를 φ = 0°에서 φ = 360° 까지 반시계 방향으로 2 RPM의 속도로 등속 회전시키는 동안, φ = 180°에 도달하면 하중을 제거하였다. 그 결과는 Fig. 10(b)에 나타나 있다.

Fig. 10

Measured each joint torque according to each joint degree (blue: without compensation, red: with compensation)

4.3 구조적 안정성 향상 검증

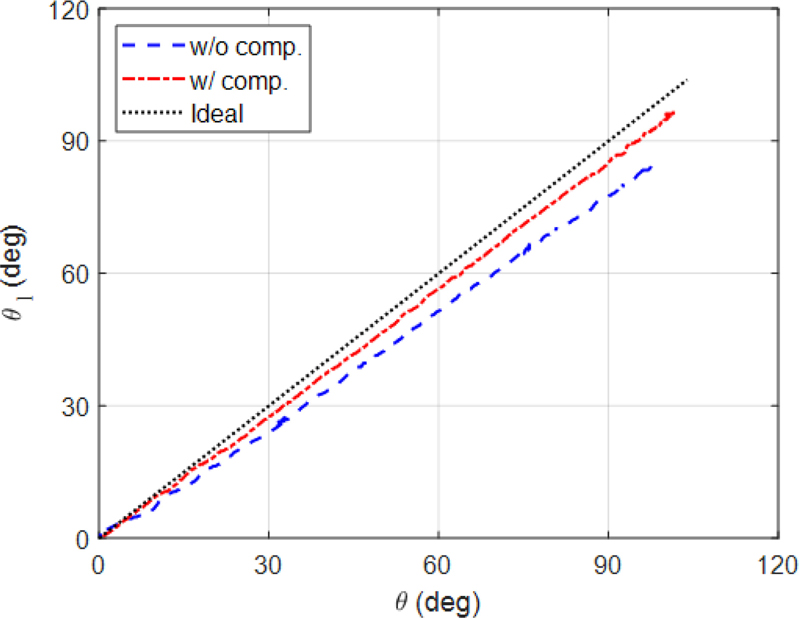
한편, 구동 실험 진행 과정에서 3D 프린팅으로 제작된 부품의 변형으로부터 발생하는 적재부 포지셔닝 오차를 발견할 수 있었다. 이 오차는 로봇의 안정성과 직접적인 연관이 있으므로, 정량적으로 평가할 필요가 있었다. 이를 위해 J_u와 J_l 두 관절에 Fig. 9과 같이 드림솔루션 사의 로터리 엔코더 AN25-Analog (Resolution: 4096PPR)가 부착되었고, 하중 1.29 kg을 들어올리는 동작에서 두 관절의 각도가 측정되었다. 그 결과는 Fig. 11에 나타나 있으며, 중력 보상 적용 전후의 포지셔닝 오차와 정확도 개선이 확인될 수 있다.

Fig. 11

Measured θl according to θ

추가적으로, 아래쪽 링크의 기어가 위로 전달하는 토크의 개선을 확인하면, 기구적 안정성 향상이 검증될 수 있다. 이를 위해 Fig. 9과 같이 기어를 연장한 링크에 로드셀이 부착되어 기어로부터 전달되는 힘이 측정되었고, 동시에 엔코더로부터 θ_l이 측정되었다. 측정된 힘은 연장된 링크의 길이 r이 곱해져 토크로 변환되었다. 그 결과, 기어의 전달 토크가 중력 보상 적용 전후 시뮬레이션과 유사하게 개선된 것을 Fig. 10(c)에서 확인할 수 있다.

5. 논의사항

앞선 4절에서는 제안하는 리프팅 장치에 대한 기본 기능을 확인하고, 적용한 중력 보상의 효과를 검증하기 위한 실험이 수행되었다. 먼저, 장치의 구동 테스트에서 크랭크의 단방향 회전만으로도 최저점과 최고점에 순간속도 0으로 반복 도달할 수 있음이 확인되었다. 이를 통해 제어 부담이 확연히 줄어들고, 반복 작업에 유리한 구조임이 입증되었다. 이때 구동에 필요한 최대 토크는 중력 보상 적용 전후 5.64와 2.53 Nm로 각각 측정되었다. 이어서 로봇을 베이스 관절에서 직접 구동하였을 때는, 중력 보상 적용 후 상승과 하강 동작 각각 필요한 최대 토크가 2.87와 3.81 Nm로 측정되었다. 두 과정의 실험값이 시뮬레이션과 유사하게 나타나, 간소화된 정역학 모델링과 중력 보상 설계의 유효성이 확인되었다. 그 후 실시된 포지셔닝 정확도 측정 실험 결과, 중력 보상 적용 전에는 θ = 98.21°와 θl = 85.58°였던 각도가 중력 보상 적용에 의해 각각 θ = 101.55°와 θl = 96.61°로 변화하였다. 이상적으로는 위아래 평행 4절 링크의 각도 θ와 θ_l이 동일하게 103.89°에 도달해야 하지만, 부품 사이의 유격과 3D 프린팅으로 만들어진 기어의 변형에 의한 오차가 확인되었다. 그럼에도 포지셔닝 오차가 18.44에서 7.35%로 감소된 결과는 아래쪽 링크의 구조적 안정성이 향상되었음을 보여준다. 마지막으로 실시된 기어의 전달 토크 측정 결과, 그 최대 크기가 중력 보상 적용 전후 2.66에서 1.23 Nm로 감소하여 아래쪽 링크의 구조적 안정성 향상이 추가적으로 입증되었다.

한편, 시뮬레이션과 실제 실험의 오차는 크게 두 가지 원인으로 분석된다. 첫째, Figs. 10(c)와 11에서 나타나는 것처럼 아래쪽 평행 4절 링크의 포지셔닝 오차로 인해 기어로 전달되는 토크가 시뮬레이션과 큰 차이를 보인다. 둘째, 장치의 구동 축에서 발생하는 마찰뿐만 아니라 케이블의 경로 변경을 위한 아이들러에서도 마찰에 의한 에너지 손실이 있는 것으로 보인다[16]. 이러한 두 가지 원인은 금속부품으로의 교체 및 제작 과정의 보완을 통해 개선될 수 있을 것으로 보인다.

본 장에서는 실험 결과의 분석을 바탕으로 소형 스케일 모델에서 중력 보상이 자재의 안정적인 이송에 효과적임을 확인하였다. 그러나, 이를 실제 건설 현장에 적용하려면 몇 가지 추가적인 검토가 필요하다. 우선, 작업 현장의 공간적 제약을 고려하여 장치의 크기와 크랭크-로커가 동작할 수 있는 공간이 확보되어야하며 그에 따라 개구부의 크기가 조정될 수 있어야 한다. 또한 실제 현장에서 다루게 될 고중량의 자재를 이송할 때 기어로 전달되는 토크를 분석하여, 기어의 변형이 방지될 수 있는 구성의 모듈 및 잇수가 선택될 필요가 있다.

6. 결론

본 논문에서는 건설 현장의 위층에 위치하며 아래층의 자재들을 작업자들 대신 반복적으로 운반하는 목적의 리프팅 장치가 제안되었다. 이 기구는 동일한 두 개의 평행 4절 링크가 기어로 구속된 1 자유도 리프트 구조에 구동을 위한 크랭크-로커가 적용되어, 구동부의 단방향 회전운동만으로 정확한 목표지점 왕복이 가능하다. 이로 인해 제어의 부담이 적고, 반복 작업에 유리하다. 여기에 단일 스프링과 케이블을 활용하여 두 개의 주요 관절을 동시에 중력 보상하는 방법이 제안되었다. 그뿐만 아니라, 리프팅 작업 한 사이클이 고려된 특별한 보상 토크 선정 방법이 제안되었다. 그 결과, 구동에 필요한 최대 토크가 5.64에서 2.53 Nm로 55.14% 감소하여, 구동기 용량을 절반 이하로 줄일 수 있었다. 또한, 포지셔닝 오차가 18.44에서 7.35%로 감소하였고, 기어로 전달되는 최대 토크가 2.66에서 1.23 Nm로 53.76% 감소하여, 아래쪽 평행 4절 링크의 처짐이 보완되고 기구의 구조적 안정성이 증가되었다. 추가적으로, 케이블의 공간 효율성 덕분에 장치의 설계 폭을 줄일 수 있었다. 결과적으로, 제안된 리프팅 장치는 실제 건설 현장에서의 적용을 위한 하중 처리 능력과 장치의 크기 및 안정성 등 여러 요소에 대한 추가 검토가 보완되어 현장에 적합한 시스템으로 발전시킨다면, 자재 인양용 개구부에 실제로 적용되어 작업자들과 협력하며[17], 작업자들이 기피하는 형틀작업에 도움을 줄 수 있을 것으로 기대된다.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant and the Institute of Information and Communications Technology Planning and Evaluation (IITP) grant funded by the Korea government under (MSIT) (Nos. NRF-2020-R1C1C1008707, RS-2023-00224546).

References

• Korea Institute of Labor Safety and Health, (2020), Construction site main floor labor intensity evaluation project. https://kilsh.or.kr/2829/
• Li, W., Lin, X., Bao, D. W., Xie, Y. M., (2022), A review of formwork systems for modern concrete construction, Structures, 38, 52-63. [https://doi.org/10.1016/j.istruc.2022.01.089]
• Schneider, S. P., (2001), Musculoskeletal injuries in construction: a review of the literature, Applied Occupational and Environmental Hygiene, 16(11), 1056-1064. [https://doi.org/10.1080/104732201753214161]
• Fung, I. W. H., Tam, V. W.-Y., Tam, C. M., Wang, K., (2008), Frequency and continuity of work?related musculoskeletal symptoms for construction workers, Journal of Civil Engineering and Management, 14(3), 183-187. [https://doi.org/10.3846/1392-3730.2008.14.15]
• Ahn, H.-J., Lee, D.-M., Lee, D.-Y., Cho, H.-H., Kang, K.-I., (2019), Development of eco-friendly light weight form for increased formwork productivity, Proceedings of the Korean Institute of Building Construction Conference, 19(1), 8-9.
• Ryu, J., McFarland, T., Banting, B., Haas, C. T., Abdel-Rahman, E., (2020), Health and productivity impact of semi-automated work systems in construction, Automation in Construction, 120, 103396. [https://doi.org/10.1016/j.autcon.2020.103396]
• Hoseo University Academic Cooperation Foundation, Haegang Industrial Co., Ltd., Seoul National University R&DB Foundation, (2019), Automatic concrete form lifting apparatus having guide member and automatic concrete form lifting method using the same, KR1020190152585.
• Lee, S. Y., Lee, K. Y., Lee, S. H., Kim, J. W., Han, C. S., (2007), Human-robot cooperation control for installing heavy construction materials, Autonomous Robots, 22, 305-319. [https://doi.org/10.1007/s10514-006-9722-z]
• Cai, S., Ma, Z., Skibniewski, M. J., Bao, S., (2019), Construction automation and robotics for high-rise buildings over the past decades: A comprehensive review, Advanced Engineering Informatics, 42, 100989. [https://doi.org/10.1016/j.aei.2019.100989]
• Inoue, K., Aoyama, H., (2023), Realization and scheduling of free spot assembly method for machine tools using cooperative industrial robots, Journal of the Korean Society for Precision Engineering, 40(4), 319-327. [https://doi.org/10.7736/JKSPE.022.130]
• Xiao, B., Chen, C., Yin, X., (2022), Recent advancements of robotics in construction, Automation in Construction, 144, 104591. [https://doi.org/10.1016/j.autcon.2022.104591]
• Wagner, H. J., Alvarez, M., Kyjanek, O., Bhiri, Z., Buck, M., Menges, A., (2020), Flexible and transportable robotic timber construction platform-TIM, Automation in Construction, 120, 103400. [https://doi.org/10.1016/j.autcon.2020.103400]
• Hou, L., Tan, Y., Luo, W., Xu, S., Mao, C., Moon, S., (2022), Towards a more extensive application of off-site construction: a technological review, International journal of construction management, 22(11), 2154-2165. [https://doi.org/10.1080/15623599.2020.1768463]
• Tuci, E., Alkilabi, M. H., Akanyeti, O., (2018), Cooperative object transport in multi-robot systems: A review of the state-ofthe- art, Frontiers in Robotics and AI, 5, 59. [https://doi.org/10.3389/frobt.2018.00059]
• Suh, J.-W., Choi, E.-C., (2019), Design and verification of a gravity-compensated tool handler for supporting an automatic hair-implanting device, IEEE Robotics and Automation Letters, 4(4), 4410-4417. [https://doi.org/10.1109/LRA.2019.2928763]
• Rivera, G., Tong, V.-C., Hong, S.-W., (2022), Improved formulation for sliding friction torque of deep groove ball bearings, Journal of the Korean Society for Precision Engineering, 39(10), 779- 789. [https://doi.org/10.7736/JKSPE.022.045]
• Inoue, K., Aoyama, H., (2023), Scheduling for Assembly Line with Human-Robot Collaboration, Journal of the Korean Society for Precision Engineering, 40(2), 163-173. [https://doi.org/10.7736/JKSPE.022.100]