자율주행 서비스 구현을 위한 4WS 기반 모바일 로봇 주행 제어 전략 연구

1. 서론

자율주행 기술의 발전과 함께 복잡한 환경에서 효율적인 경로 계획 및 정확한 경로 추종의 중요성이 날로 증가하고 있다. 특히 산업 현장이나 물류 환경과 같이 좁은 공간 내 정밀한 이동이 요구되는 상황에서, 기존의 Ackermann 조향 시스템은 제한된 기동성으로 인해 한계를 보인다. 이러한 문제를 해결하기 위해 4륜 조향(4 Wheel Steering, 4WS) 시스템이 주목받고 있으며, 4WS 시스템의 복잡한 운동학적 특성을 반영한 효과적인 경로 계획 및 추종 알고리즘이 지속해서 연구되고 있다[1-3].

기존의 경로 계획 알고리즘 중 A*는 그 효율성과 완전성으로 인해 널리 사용되어 왔으나, Non-holonomic 제약 조건을 가진 차량의 운동학적 특성을 고려하지 못한다는 한계가 있다. 이를 보완하기 위해 제안된 Hybrid A* 알고리즘은 연속적인 상태 공간 표현이 가능하고 자동차와 같은 로봇의 Non-holonomic 제약 조건을 수용할 수 있다는 장점이 있다[5,6].

경로 추종 시 4WS 로봇 주행 제어를 위한 다양한 접근 방식이 제안되었다[7-11]. 그러나 이러한 방법들은 복잡한 환경 내 경로 계획과 추종을 동시에 고려하지 않았다는 한계가 있다.

본 연구에서는 Hybrid A* 알고리즘을 4WS 시스템의 특성에 맞게 확장하고, 이를 Model Predictive Control (MPC)과 결합하여 효율적인 경로 계획 및 추종 방법을 제안한다. 또한, 차량의 운동 상태에 따라 적응적으로 제어 모드를 전환하는 방식을 도입하여 시스템의 유연성과 효율성을 높였다. 본 논문의 기여는 다음과 같다: 첫째, 경로 계획 및 최적화를 통해 4WS 시스템의 운동학적 특성을 고려한 Hybrid A* 알고리즘을 적용하여, 효율적인 경로 계획 실시한다. 둘째, 모델 예측 제어(MPC)를 이용하여 계획된 경로를 정확하게 추종하는 제어 시스템 구현한다. 셋째, 차량의 운동 상태에 따라 세 가지 모드(일반 주행, 회전, 평행 이동)로 전환되는 적응형 역기구학 알고리즘을 적용하여 다양한 상황에 대응할 수 있는 유연한 제어 전략 제안한다.

본 연구에서 제안하는 방법은 복잡한 환경에서 4WS 시스템의 장점을 최대한 활용하면서, 효율적인 경로 계획과 정확한 경로 추종을 동시에 달성할 수 있다는 점에서 기존 연구와 차별화 된다. 또한 좁은 공간에서의 정밀한 이동이 요구되는 실제 산업용 로봇 환경을 MATLAB으로 적용하여, 검증하였으며 4WS의 자율주행 성능을 향상시킬 수 있을 것으로 기대된다.

본 논문의 구성은 다음과 같다. 2장에서 4WS 로봇 운동학 및 기구학에 대해 서술하고, 3장에서 NMPC 제어기 설계 및 경로 계획과 제어 전략에 대해 설명한다. 이후, 4장과 5장에서는 각각 시뮬레이션을 통한 추종 성능 검증 및 비교 결과를 제시하고 논 논문의 결론을 내린다.

2. 4WS 로봇 운동학

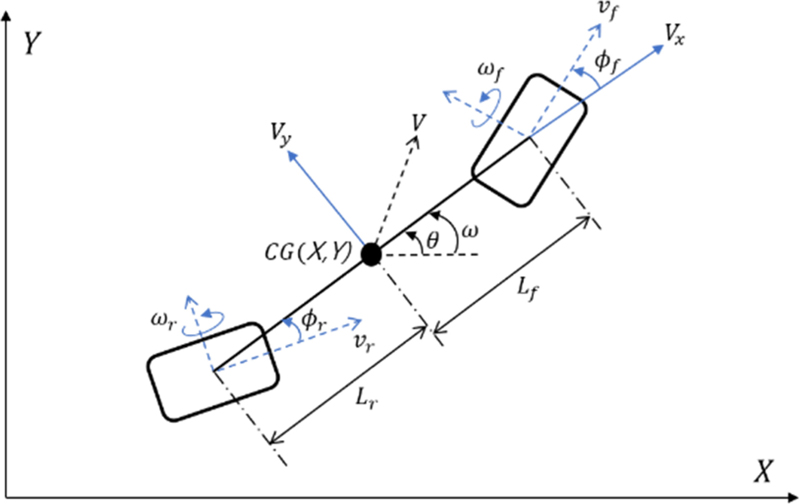
4개의 스티어링 휠을 가진 로봇은 공장 내 이동 시 안정성을 고려해 낮은 가속 및 저속에서 이동하도록 제한한다. 또한 강체 및 Non-slip 조건으로 가정한 4WS의 동적 모델은 Fig. 1과 같이 2DOF Bicycle Model로 나타낼 수 있다[1,4].

로봇은 주행 시 2.1절의 3가지 모드를 기반으로 목표 지점까지 주행한다.

Fig. 1

Kinematic model

2.1 역기구학

Fig. 2는 4WS 로봇의 개념도이다. 로봇의 모션 제어를 위해서는 제어 타겟으로 주어진 로봇의 속도(V)와 각속도(ω)를 구현하기 위한 조향각(ϕ_f, ϕ_r)과 휠속도(ω_f, ω_r)가 필요하고, 이는 4WS의 역기구학에 의해 계산된다. 각각의 제어 전략에 따른 4WS의 역기구학은 일반 주행 모드, 회전 모드, 평행 이동 모드로 구분하여 유도할 수 있다.

Table 1

Kinematics parameter

Fig. 2

4WS robot

2.1.1 일반 주행 모드 역기구학

조향 시 전륜과 후륜의 조향 방향이 반대가 되어 로봇의 회전 반경을 줄일 수 있다. 일반 주행 모드는 로봇의 선속도(V_x)와 각속도(ω)만을 사용하여 주행하고, 각 휠의 최대 조향각은 30°로 제한한다.(-30° < ϕ_f, ϕ_r < 30°)

$\[ {\varphi }_f={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\omega \left(L_f+L_r\right)/V_x\right) \]$

(1)

$\[ {\varphi }_r=-{\varphi }_f=\varphi \]$

(2)

$\[ {\omega }_f=V_x/r\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_f \]$

(3)

$\[ {\omega }_r={\omega }_f=\omega \]$

(4)

2.1.2 회전 모드

회전 모드를 실행하기 위한 조건이 만족되면 로봇이 정지한 뒤 휠을 정해진 각도에 따라 조향하고, 각속도(ω)를 만족하기 위해 휠 속도를 제어한다.

$\[ {\varphi }_f=\left\{\begin{array}{cc}if V_x=0,& \pi /2\\ else,& {\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\omega \left(L_f+L_r\right)/V_x\right)\end{array}\right. \]$

(5)

$\[ {\varphi }_r=-{\varphi }_f=\varphi \]$

(6)

$\[ {\omega }_f=\left\{\begin{array}{cc}if V_x=0,& \omega L_f/r\\ else,& V_x/r\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_f\end{array}\right. \]$

(7)

$\[ {\omega }_f={\omega }_r \]$

(8)

2.1.3 평행 이동 모드

회전 모드에서 목표 지점과의 각도가 일치되면 현재 자세를 유지한 채 로봇의 속도(V)만을 사용하기 위한 휠 속도를 제어한다.

$\[ {\varphi }_f=atan\left(V_y/V_x\right) \]$

(9)

$\[ {\varphi }_r={\varphi }_f=\varphi \]$

(10)

$\[ {\omega }_r={\omega }_f=\omega \]$

(11)

$\[ V=\pm \left(V_x\right)/r\sqrt{V_x^2+V_y^2} \]$

(12)

2.1.4 순기구학

조향각(ϕ_f, ϕ_r)과 휠 속도(ω_f, ω_r)를 입력으로 받아 로봇의 속도(V)와 각속도(ω)를 계산하며, 다음과 같이 나타낼 수 있다.

$\[ V_x=0.5*r\left({\omega }_f\mathrm{c}\mathrm{o}\mathrm{s}\left({\varphi }_f\right)+{\omega }_r\mathrm{c}\mathrm{o}\mathrm{s}\left({\varphi }_r\right)\right) \]$

(13)

$\[ V_y=0.5*r*\left({\omega }_f\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_f\right)+{\omega }_r\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_r\right)\right) \]$

(14)

$\[ \omega =\left({\omega }_f\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_f\right)-{\omega }_r\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_r\right)\right)*r/\left(L_f+L_r\right) \]$

(15)

3. NMPC 기반 제어 시스템 설계

3.1 Nonlinear Model Predictive Control (NMPC)

4WS 조향 시스템의 운동학적 특성을 반영하여 효과적으로 제어하기 위해 비선형 MPC (NMPC) 제어가 사용되었다[11,12].

NMPC 제어기는 비선형 이산 시간 모델을 사용하여 로봇의 동역학식을 다음과 같이 표현한다.

$\[ x\left[k+1\right]=f\left(x\left[k\right],u\left[k\right]\right) \]$

(16)

여기서,

$\[ x\left[k\right]={\left[x,y,\theta \right]}^T \]$

(17)

$\[ u\left[k\right]={\left[v_x,v_y,\omega \right]}^T \]$

(18)

정리하면,

$\[ x\left[k+1\right]=x\left[k\right]+M\left(\theta \left[k\right]\right)*u\left[k\right]*T_s \]$

(19)

다음과 같이 나타낼 수 있다.

M(θ[k])는 로봇의 현재 방향각에 따른 회전 행렬을 나타낸 것이며[17], T_s는 샘플링 시간에 해당한다.

Table 2에 제시된 제약 조건을 반영한 속도 오차항은 e_vx = v_xref − v_x, e_vy = v_yref − v_y, e_ω = ω_ref − ω로 정의되고, 제어기의 비용 함수를 정의하기 위한 식은 다음과 같다.

Table 2

Robot parameter & control constraints

$\[ J={\omega }_1{e}_{v_x}^2+{\omega }_2{e}_{v_v}^2+{\omega }_3{e}_{\omega }^2+r_1\mathrm{\Delta }{u}_1^2+r_2\mathrm{\Delta }{u}_2^2+r_3\mathrm{\Delta }{u}_3^2 \]$

(20)

여기서, ω₁-ω₃, r₁-r₃은 가중치, ∆u₁-∆u₃은 식(18)에 제시한 제어 입력 간 차이이다.

로봇의 상태 변수(x[k]) 및 출력 변수(x[k+1]) 모두 위칫값으로 사용하나, 제어기 내 입력 변수는 (v_x, v_y, ω)로 정의되어, 2.1절에 제시된 4WS 조향 시스템의 운동학적 방정식을 이용한 로봇의 실제 위칫값을 계산한다.

해당 제어기의 적절한 입력 및 출력 예측값을 포함하면, 식(20)은

$\[ J=\sum _{k=1\sim p}^k {‖y\left(k\right)-r\left[k\right]‖}_Q^2+\sum _{k=1\sim m}^k \left({‖u\left(k\right)‖}_S^2-{‖\mathrm{\Delta }u\left[k\right]‖}_R^2\right) \]$

(21)

다음과 같이 나타낼 수 있다. 여기서, y[k]는 로봇의 예측된 위치이고 r[k]는 참조 궤적, u[k]와 ∆u[k]는 제어 입력 및 변화량을 나타낸다.

NMPC는 이러한 과정들을 통해 로봇의 위치와 방향을 직접 제어할 수 있다. 특히, y 방향 속도(v_y)를 별도의 입력 변수로 포함함으로써, 필요에 따라 측면 이동을 가능하게 하는 4WS의 조향 특성을 반영하고 있다.

3.2 경로 계획

기본적인 경로 계획은 Hybrid A* 알고리즘을 적용하여 목적지까지 경로를 생성한다. 기본적으로 널리 사용되는 A* 알고리즘을 연속 상태 공간에 적용할 수 있도록 확장한 방법이다. 각 지점들 간 연속적인 4WS 로봇의 위치(x, y, θ)를 고려하여, 운동학적 제약 조건을 만족하는 경로로 생성하는 방법으로 목표 지점까지의 경로를 생성한다[6-8].

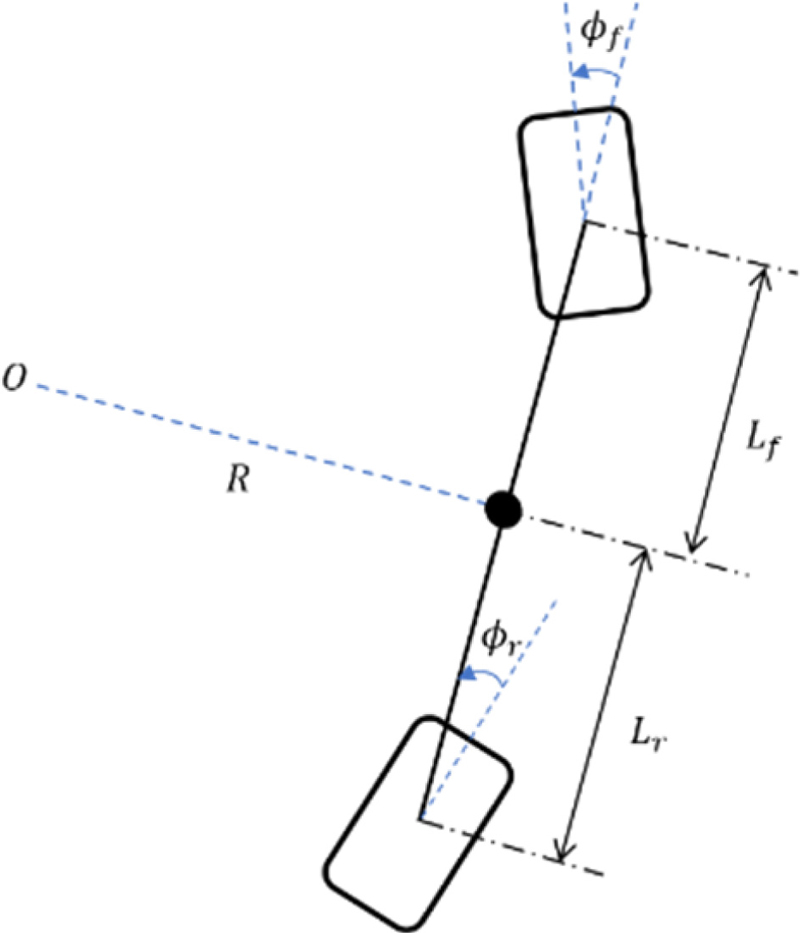
Fig. 3을 참고하여 로봇의 최소 회전 반경(R)은 식(22)과 같이 간단히 나타낼 수 있다.

$\[ R=\left(L_f+L_r\right)/\mathrm{t}\mathrm{a}\mathrm{n}\left({\varphi }_f+{\varphi }_r\right) \]$

(22)

Fig. 3

Turning radius of bicycle model

Fig. 4

4WS control system

Fig. 5

Experimental environment

계산된 최소 회전 반경을 통해, 목표 지점까지의 위치 및 방향을 고려한 기본적인 경로가 생성된다. 이후, Table 1에 제시된 설정값과 3.3절에 제시할 제어 전략에 따라 최적화되어 식(19)의 참조 궤적 값으로 사용된다.

3.3 제어 전략

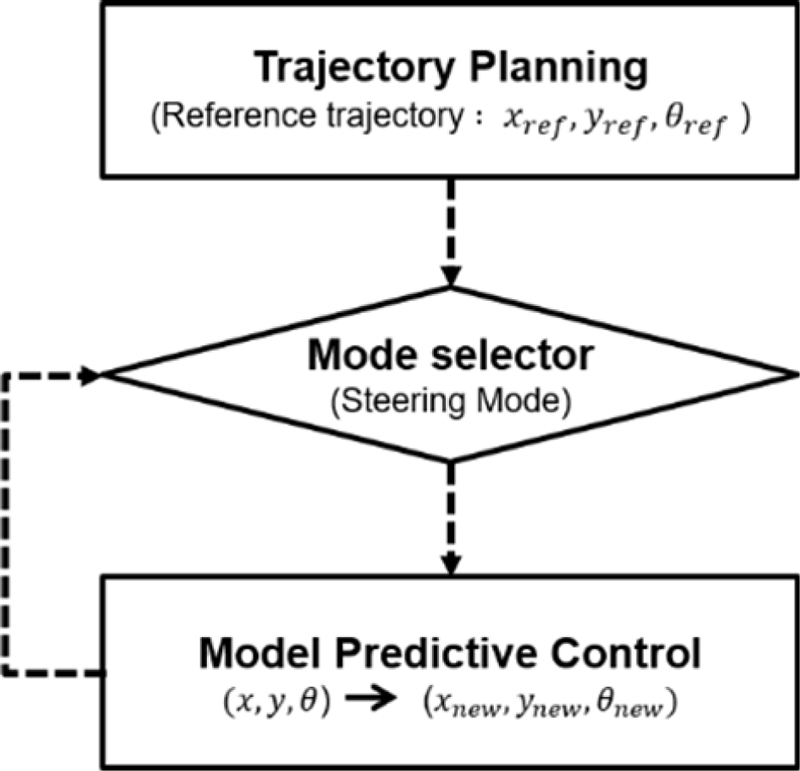
4WS 로봇의 내비게이션 시스템 구조는 Fig. 6과 같다. 모드에 따라, 식(1)부터 식(12)를 사용하여 현재 위치가 계산되면, 목표 지점과의 위치에 따라 모드 전환을 통해 필요한 주행 모드를 결정한다.

Fig. 6

Comparison of path planning algorithms

제안하는 제어 전략은 작업자가 설정한 지점 반경까지 일반 주행 모드로 이동한 뒤, 해당 지점에서 정지하여 회전 모드를 통해 목표 지점과의 각도를 일치시킨다. 이후 평행 이동 모드를 사용하여 목표 지점까지 평행 이동을 하도록 한다.

주행 중 식(1)부터 식(15)를 따르며, 목표 지점과의 거리 및 각도 차이에 따라 적응적으로 모드를 전환한다.

4. 시뮬레이션 및 결과

4.1 시뮬레이션 환경

제안한 제어 전략 및 경로 추종 성능 검증을 위해 Fig. 5(a)의 실제 대규모 물류 창고의 특성을 반영하여[13], 폭이 좁고 긴 통로와 선반들로 구성된 복잡한 구조를 MATLAB으로 구성하였다. 로봇은 3.3절에 제시한 제어 전략에 따라 Fig. 5(b) 환경 내 주행을 실시한다.

4.1.1 경로 생성 및 최적화 결과

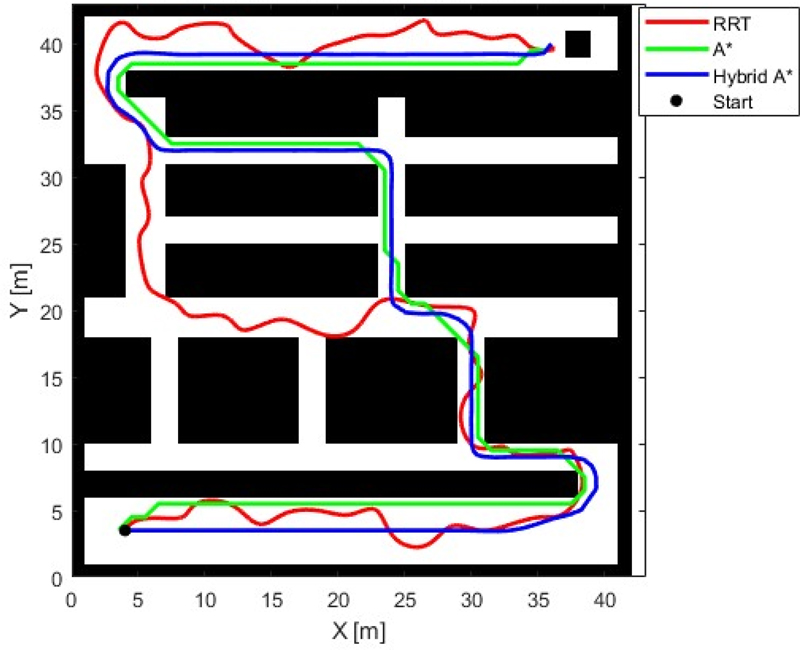
Fig. 6은 RRT (Rapidly-exploring Random Tree), A* 그리고 Hybrid A* 기반의 경로 계획 결과를 보여준다. Table 3은 각 경로 계획 알고리즘에 따른 목표 지점까지의 주행 거리를 나타낸다.

Table 3

Length of path planning algorithms

RRT 경로 계획 알고리즘을 이용하여 경로 계획을 한 경우, RRT의 특성상 무작위의 경로가 생성되어 목표 지점까지 이동거리가 가장 길게 나타나는 것을 볼 수 있다. 반면, A* 경로 계획 알고리즘을 사용하여 경로 계획을 했을 때는 효율적인 경로 계획을 하였으나 로봇의 회전 반경이 전혀 고려되지 않아 장애물에 가까운 주행 경로를 생성하는 것을 확인할 수 있다.

위와 같은 문제점들을 보완한 Hybrid A* 경로 계획 알고리즘은 로봇의 회전 반경과 장애물과의 거리 모두를 고려한 결과를 나타낸다.

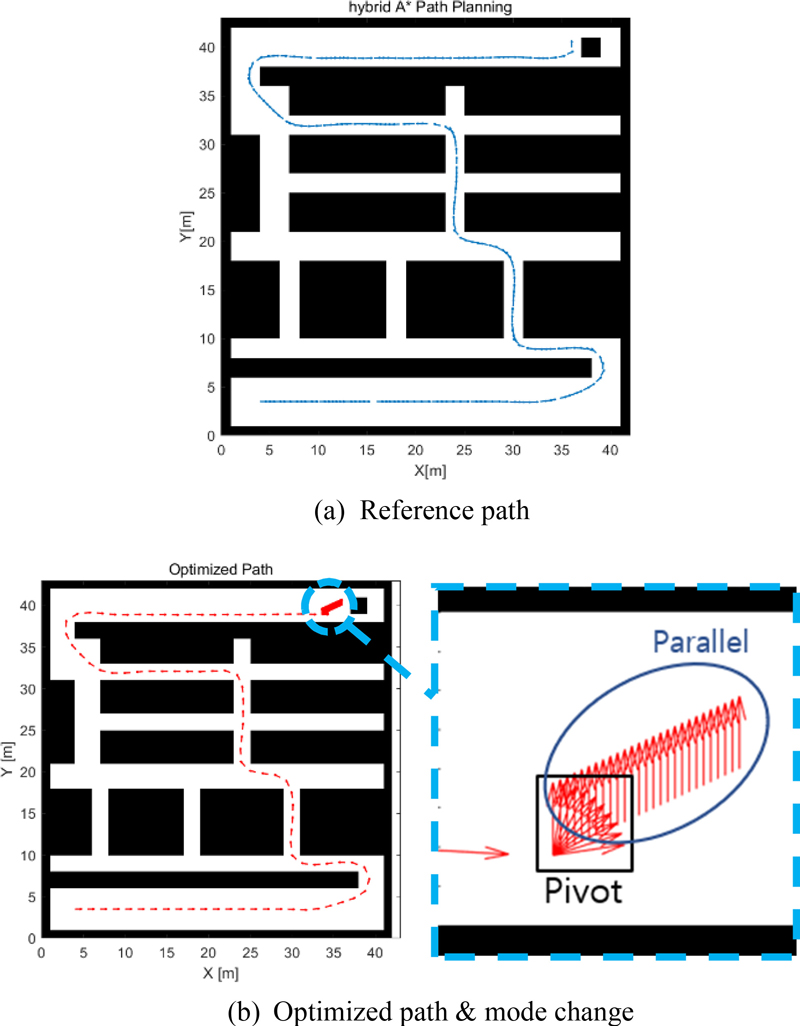
Hybrid A* 통해 생성된 경로를 로봇의 위치 및 방향을 고려하여 재시각화 한 결과는 Fig. 7(a)와 같다. 이는 로봇의 회전 반경만 고려한 결과이며, 3.3절에 제시한 제어 전략을 참고하여 Fig. 7(b)에서 회전 모드와 직선 모드를 고려한 경로를 추가적으로 생성하였다. 이후 일정 간격으로 경로를 재생성 하여 제어 안정성을 높이는 최적화를 실시했다.

Fig. 7

Path optimization

4.2 경로 추종 성능 평가

로봇은 Hybrid A* 알고리즘으로 생성된 경로를 바탕으로, 제안하는 제어 전략 및 시스템 제약 조건을 적용하여 정확하게 목표 지점까지 이동하는 것을 목표로 한다.

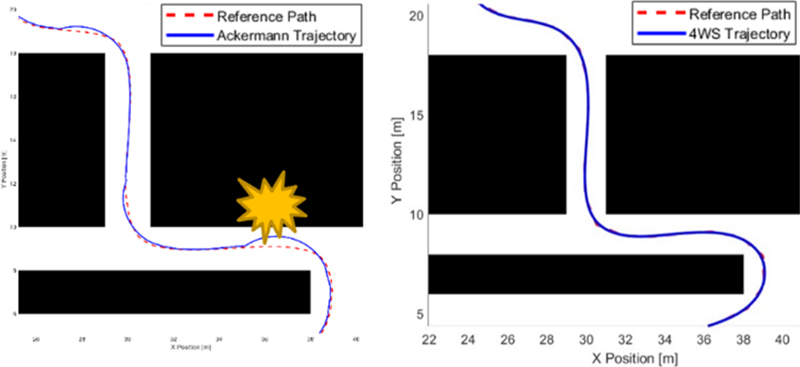
Fig. 8은 Ackermann 조향 메커니즘과 4WS 조향 메커니즘의 주행 궤적을 비교한 결과를 보여준다. Ackermann 조향 메커니즘으로 주행 시 회전 반경이 제한되어 장애물과의 충돌이 발생하지만, 4WS 조향 메커니즘으로 주행할 때는 회전 반경의 제약 조건이 완화되어 복잡한 환경에서도 원활한 주행이 가능함을 보여준다.

Fig. 8

Comparison of tracking performance by driving type

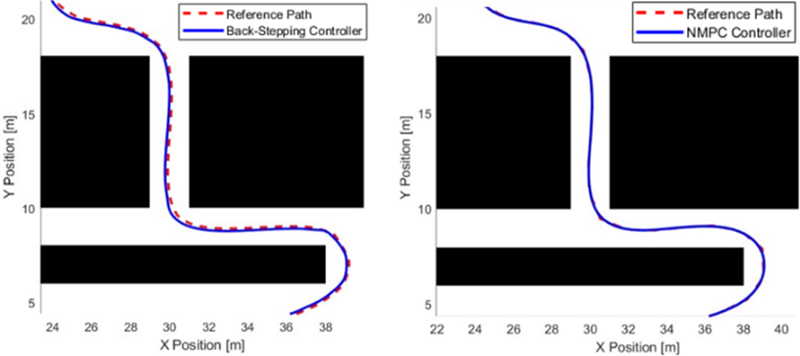
Fig. 9는 동일한 4WS 운동학적 특성을 참고하여 Backstepping 제어기와 NMPC간 실험 결과를 나타냈다. 두 제어기 모두 비선형 제어 방법으로 Hybrid A*에 의해 계획된 경로를 성공적으로 추종하고 있지만, 본 연구에서 사용한 NMPC가 보다 나은 경로 추종 성능을 갖는 것을 Table 4에 나타난 각 항목을 통해 확인할 수 있다.

Fig. 9

Comparison of tracking performance by controller

Table 4

Path tracking performance

평균위치오차, RMS오차, 오차 최대치 등의 성능 비교를 통해 NMPC 기반 제어가 Back-stepping 제어 방법[14-16]에 비해 향상된 경로 추종 성능을 보여준다.

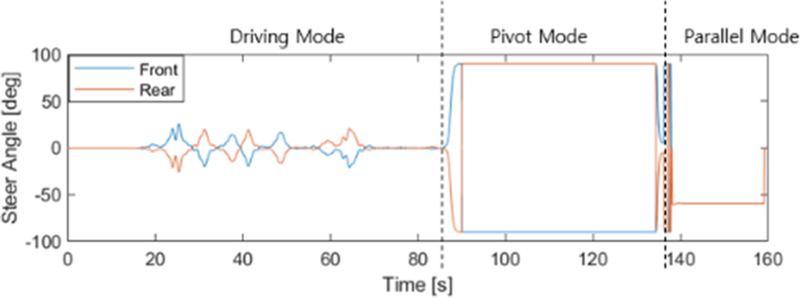
Figs. 10과 11은 목표 지점까지 주행하면서 각각의 결괏값들을 나타낸다. 각 제어 모드에 따를 역기구학에 기반한 제어가 실행되는 것을 확인 할 수 있고, 제안하는 알고리즘을 기반으로 성공적인 내비게이션이 수행되는 것을 확인 할 수 있다.

Fig. 10

Steering angle change

Fig. 11

Velocity & acceleration

5. 결론

협소한 공간 내에서 로봇의 주행 성능을 향상하기 위한 4WS 기반 모바일 로봇의 내비게이션 알고리즘을 설계하였다. 경로 계획 시 모드 전환 및 최적화를 실시한 경로를 바탕으로, NMPC 제어기를 설계하였다. 로봇의 위치 제어를 위한 기준 입력은 4WS 로봇의 주행 모드에 따른 역기구학을 이용하여 계산하였다. 제안하는 알고리즘의 성능을 검증하기 위해 협소한 환경을 갖는 물류 창고 시나리오 하에서 MATLAB 시뮬레이션을 실시하였다. 4WS 로봇이 정의된 주행 모드에 맞게 제어를 실행하며 성공적인 내비게이션을 수행하는 것을 확인 할 수 있었다. 다만, 본 연구는 시뮬레이션 기반으로 그 가능성을 구현하는 데 그쳐 한계가 있다. 따라서, 향후 연구 과제로 4WS 모바일 로봇 플랫폼을 개발하여 제안하는 제어 전략의 적용을 통한 최적화 및 개선을 수행하여 실환경 적용성을 높이는 연구를 수행할 예정이다.

Acknowledgments

이 연구는 2024년도 산업통상자원부 및 산업기술기획평가원(KEIT) 연구비 지원에 의한 연구임(RS-2024-00423899).

References

• Wang, D., Qi, F., (2001), Trajectory planning for a four-wheelsteering vehicle, Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), 3320-3325.
• Dai, P., Katupitiya, J., (2015), Force control of a 4WS4WD vehicle for path tracking, IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 238-243. [https://doi.org/10.1109/AIM.2015.7222538]
• Injarapu, A. S. H. H. V., Gawre, S. K., (2017), A survey of autonomous mobile robot path planning approaches, International Conference on Recent Innovations in Signal Processing and Embedded Systems (RISE), 624-628. [https://doi.org/10.1109/RISE.2017.8378228]
• Chen, X., Peng, Y., Hang, P., Tang, T., (2020), Path tracking control of four-wheel independent steering electric vehicles based on optimal control, 39th Chinese Control Conference (CCC), 5436-5442. [https://doi.org/10.23919/CCC50068.2020.9189047]
• Dolgov, D., Thrun, S., Montemerlo, M., Diebel, J., (2008), Practical search techniques in path planning for autonomous driving, Ann Arbor, 1001(48105), 18-80.
• Petereit, J., Emter, T., Frey, C. W., Kopfstedt, T., Beutel, A., (2012), Application of hybrid A* to an autonomous mobile robot for path planning in unstructured outdoor environments, ROBOTIK 2012; 7th German Conference on Robotics, 1-6.
• Sedighi, S., Nguyen, D.-V., Kuhnert, K.-D., (2019), Guided hybrid A-star path planning algorithm for valet parking applications, 5th international conference on control, automation and robotics (ICCAR), 570-575. [https://doi.org/10.1109/ICCAR.2019.8813752]
• Dang, C. V., Ahn, H., Lee, D. S., Lee, S. C., (2022), Improved analytic expansions in hybrid A-star path planning for nonholonomic robots, Applied Sciences, 12(12), 5999. [https://doi.org/10.3390/app12125999]
• Hakima, A., Ameli, S., (2010), Designing a fuzzy logic controller to adjust the angle of tires in four wheel steering vehicles, 2010 11th International Conference on Control Automation Robotics & Vision, 2208-2213. [https://doi.org/10.1109/ICARCV.2010.5707765]
• Yim, S., (2020), Comparison among active front, front independent, 4-wheel and 4-wheel independent steering systems for vehicle stability control, Electronics, 9(5), 798. [https://doi.org/10.3390/electronics9050798]
• Nguyen, N. T., Gangavarapu, P. T., Mandel, N., Bruder, R., Ernst, F., (2024), Motion planning for 4WS vehicle with autonomous selection of steering modes via an MIQP-MPC controller, IEEE International Conference on Robotics and Automation (ICRA), 9765-9771. [https://doi.org/10.1109/ICRA57147.2024.10610461]
• Sotnikova, M. V., Veremey, E. I., (2013), Dynamic positioning based on nonlinear MPC, IFAC Proceedings Volumes, 46(33), 37-42. [https://doi.org/10.3182/20130918-4-JP-3022.00058]
• The Standard, Amazon to open London hub. https://www.standard.co.uk/business/business-news/amazon-to-openlondon-hub-7965332.html
• Kumar, U., Sukavanam, N., (2008), Backstepping based trajectory tracking control of a four wheeled mobile robot, International Journal of Advanced Robotic Systems, 5(4), 38. [https://doi.org/10.5772/6224]
• Tu, X., Gai, J., Tang, L., (2019), Robust navigation control of a 4WD/4WS agricultural robotic vehicle, Computers and Electronics in Agriculture, 164, 104892. [https://doi.org/10.1016/j.compag.2019.104892]
• Tan, Q., Qiu, C., Huang, J., Yin, Y., Zhang, X., Liu, H., (2022), Path tracking control strategy for off-road 4WS4WD vehicle based on robust model predictive control, Robotics and Autonomous Systems, 158, 104267. [https://doi.org/10.1016/j.robot.2022.104267]
• Klancar, G., Zdesar, A., Blazic, S., Skrjanc, I., (2017), Wheeled mobile robotics: From fundamentals towards autonomous systems, Butterworth-Heinemann.