제조 환경에서 회귀 분석 기반의 공구 수명 예측 모델 개발

1. 서론

절삭가공에서 공구 수명 예측은 제조업의 생산성, 품질, 비용 절감과 직결되는 중요한 연구 주제이다. 현대 제조 환경에서는 고속 가공, 자동화 시스템, 다양한 소재의 등장으로 공구의 마모와 이에 따른 교체 주기가 매우 중요한 요소로 작용하고 있다. 공구가 마모되면 가공 정확도가 저하되고, 제품의 표면 거칠기나 치수 정밀도가 떨어져 불량이 발생할 가능성이 높아진다. 이는 가공 시간과 비용을 증가시키는 요인이며, 불필요한 공구 교체는 생산성 저하로 이어질 수 있다[1].

특히 황삭가공은 많은 양의 재료를 짧은 시간에 제거하기 위해 높은 소재제거율을 사용하는 공정으로 과도한 절삭력에 의한 공구의 마모가 심하고, 공구 파손이 빈번하게 일어난다[2]. 황삭가공 중 공구가 마모되거나 파손될 경우 작업 중단이 발생하여 생산 공정의 흐름이 끊기고, 이는 생산 비용의 증가와 납기 지연으로 이어질 수 있다. 더욱이, 황삭가공은 일반적으로 절삭력의 변화폭이 커 공구가 갑작스럽게 파손되면서 안전 문제까지 발생할 수 있다. 이러한 이유로 공구 수명을 예측하고 관리하는 것은 황삭가공에서 특히 중요하다.

공구 수명 예측에 대한 기존 연구들은 다양한 방식으로 접근하여, 공구 수명을 연장하고 가공 효율을 높이는데 기여해 왔다. 이들 연구는 주로 공구 마모 예측, 수명 추정, 그리고 가공 조건에 따른 공구 성능 평가에 중점을 두고 있고, 이를 위해 전통적인 테일러(Talyor) 공구 수명 방정식에 기반한 경험적 모델 기반 연구 및 공구 마모 데이터를 기반으로 한 통계적 방법이 주로 연구되어 왔으며, 최근에는 기계학습 및 딥러닝 알고리즘을 적용하여 공구 수명을 예측하려는 시도가 많아지고 있다[3-9]. 이와 함께 학습데이터 확보 및 실시간 모니터링을 위한 공구에 부착된 센서를 통해 온도, 진동, 힘 등의 데이터를 실시간으로 수집하고, 이를 바탕으로 공구 마모 상태를 즉시 평가하여 공구 수명을 예측하는 연구들이 활발히 진행되고 있다[10,11]. 이와 같이 기존 연구들은 경험적 모델, 통계적 방법, 머신러닝 알고리즘 등을 통해 공구 수명을 예측하는 다양한 접근법을 제시해왔다. 공구 수명은 플랭크 마모 등의 방법으로 측정되며, 임계치를 초과하면 한계 수명으로 정의되지만, 실제로 이러한 방식으로 공구 수명을 예측하기는 어렵다. 테일러의 실험적 공구 수명은 절삭 속도에 크게 의존하는 것으로 알려져 있지만, 다양한 가공 조건에 따른 공구 수명을 예측해야 신뢰성을 확보할 수 있다. 또한, 실제 현장에서는 가공 공정 중 모니터링 시스템을 통해 공구 마모를 정확하게 예측하고 공구를 교환하는 경우가 드물며, 대부분 작업자의 경험에 의존해 공구 교환이 이루어지고 있다.

머신러닝과 데이터 기반 분석이 공구 수명 예측의 새로운 돌파구로 주목받고 있으며, 이는 더 많은 데이터를 통해 더 정교하고 신뢰성 있는 모델로 발전할 수 있어 본 연구에서는 현장 데이터를 기반으로 회귀 모델을 이용한 머신러닝 기법을 활용하여 공구 수명 예측 방법을 제시하고 성능을 검증하였다. 이를 통해 제조 현장에서 적용 가능한 실질적인 솔루션을 제공하고, 공구 사용의 효율성을 높여 생산성을 향상시킬 수 있는 방안을 마련하였다.

2. 데이터 수집 및 인자 분석

2.1 데이터 수집

공구의 마모나 결손이 가공하는 제품의 품질에 직접 영향을 주는 것은 물론이다. 최근과 같이 가공의 자동화가 진전하고 또 생산성을 중시하는 상황에서는 공구 수명을 어떻게 적절히 판단하고 관리하는가가 중요한 문제가 된다.

일반적으로 현장에서 공구 수명을 판정하는 항목으로는 표면조도, 마모, 절삭음, 버, 채터링, 진동, 불꽃 등이 사용되고 있다. 이론적인 ISO 추천기준인 마모량에 따른 수명 판정은 실제 현장에서 사용이 불가능하다. 공구 수명을 판정하는 검출 항목으로서 공구의 절손이나 결손을 자동적으로 판단하는 예는 아직 적지만 이것은 공구 절손과 같은 순간적인 현상에 대응할 수 있는 고신뢰성 시스템이 아직은 충분히 보급되지 않고 있기 때문이다. 이러한 수명 판정은 아직까지 눈, 귀로 판단하는 작업자의 직감력과 경험에 의존하는 방법이 여전히 강하다고 여겨진다.

공구 수명에 영향을 미치는 인자들은 가공 중 발생하는 다양한 물리적, 환경적 요인들로 구성되며, 이들은 공구의 마모와 손상 속도에 직접적인 영향을 미치게 된다. 특히, 절삭속도, 이송속도, 절삭 깊이와 같이 작업자가 설정하는 직접적인 가공조건 및 공구, 소재 재질, 공구의 기하학적 형상 및 크기 등도 중요한 인자로 고려되어야 한다.

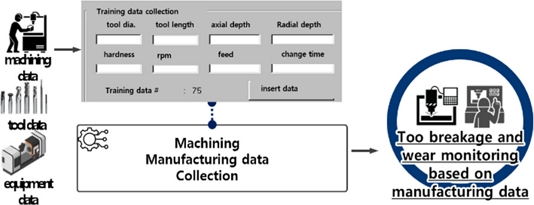
본 연구의 목표는 NC가공에 있어서 현장의 데이터를 축척해 이 데이터를 이용한 공수 수명을 예측하는 시스템을 개발하는 것이다. 기계가공에 있어서 가공환경은 범위가 너무 방대하기 때문에, 어느 정도 범위를 한정시킬 필요가 있다. 공구 수명이 특히 중요한 가공 공정 중 하나는 절삭량이 많은 황삭가공이며, 본 연구에서는 사출 금형의 황삭가공을 대상으로 공구 수명 예측 문제를 다룬다. 사출금형 황삭가공 현장에서는 파삭재 및 공구 소재는 크게 바꾸지 않고, 제품의 형상 크기에 따라 공구의 치수를 변경하여 가공하는 것이 일반적이다. 따라서 본 연구에서는 KP4M 소재를 초경 공구로 가공하는 업체에서 황삭가공 공정 중 작업자가 조정 가능한 공구 수명에 직접적인 영향을 미치는 공구 직경, 공구 길이, 축 방향 깊이, 반경방향 깊이, 회전수, 이송 속도를 주요 인자로 설정하고 Fig. 1과 같이 현장에 DB를 구축하여 작업자가 입력한 데이터를 수집하였다. 공구 수명은 작업자가 현장에서 공구를 교환하는 시점을 공구 수명으로 정의하였으며, 현장 기반의 데이터를 총 113개 확보하였다.

Fig. 1

Machining data collection

2.2 데이터 상관관계 분석

수집된 데이터는 이상치를 제거하고 총 113개로 이 중 102개는 학습에 사용하고 11개는 검증을 위한 데이터로 구분하였으면, 학습 데이터의 통계적 기술량은 Table 1과 같다.

Table 1

Statistical description of learning data

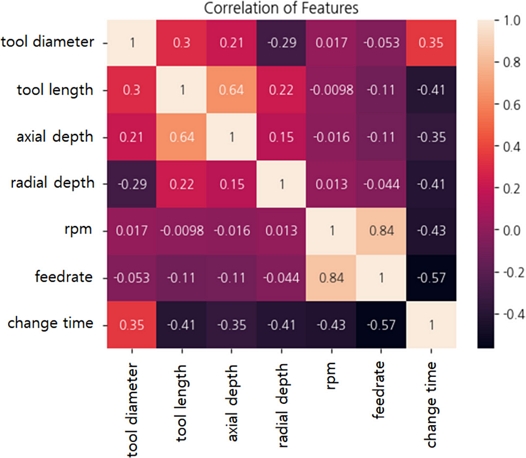
공구교환시간, 즉 공구 수명에 영향을 미치는 인자들의 상관계수는 Fig. 2와 같으며 이송속도와 회전수는 강한 양의 상관관계를 갖는 다는 것을 확인할 수 있다. 이송속도와 회전수는 식(1)과 같이 기술되며, 회전수가 증가할수록 동일한 이송량을 유지할 경우, 이송 속도도 비례적으로 증가하게 된다. 이러한 관계로 인해 이송속도와 회전수는 높은 상관관계를 가지게 되고 두 변수를 모두 회귀모델에 사용할 경우 공선성 문제를 피할 수 없게 된다.

$\[ \begin{array}{c}\text{Feed }\left(\mathrm{m}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n}\right)=\text{Feed per Revolution }\left(\mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}\right)\\ \times \text{Number of revolution }\left(\mathrm{r}\mathrm{e}\mathrm{v}/\mathrm{m}\mathrm{i}\mathrm{n}\right)\end{array} \]$

(1)

Fig. 2

Correlation between factors

식(2)의 분산 팽창 계수(Variance Inflation Factor, VIF)를 계산하여 공선성 문제를 진단하였을 때도 회전수와 이송속도는 각각 83, 70의 높은 값을 갖는다는 것을 확인하였다.

$\[ \begin{array}{cc}& \mathrm{V}\mathrm{I}\mathrm{F}=1/\left(1-{\mathrm{R}}^2\right)\\ & \left(\text{Where,}{\mathrm{ }\mathrm{R}}^2 : \text{coefficient of determination}\right)\end{array} \]$

(2)

3. 회귀 분석 및 모델 개발

현장 기반으로 확보한 공구 수명 데이터는 연속적인 값을 가지며, 이를 설명하는 가공 조건 변수들도 연속적인 수치형 데이터로 이루어져 있다. 회귀모델은 종속변수와 독립변수 간의 연속적인 관계를 학습하는 데 적합한 통계적 기법으로, 가공 조건과 공구 수명 간의 상관관계를 정량적으로 분석할 수 있는 방법으로 본 연구에서는 공구 수명 예측을 위해 회귀모델을 사용하였다. 회귀 모델의 정확도를 높이기 위해서는 변수들 간의 다중 공선성 문제를 해결하는 것이 중요하다. 공선성이 높을 경우, 변수들 간의 상관관계로 인해 회귀 계수의 추정치가 불안정해지고 모델의 예측 성능이 저하될 수 있다. 이를 해결하기 위해 상관계수, 분산 팽창 계수, 주성분 분석, 정규화 등 다양한 방법들이 제시되고 있지만, 아직까지 이 문제를 완벽히 해결할 수 있는 방법이 제시되고 있지 않다. 본 연구에서는 가공에 대한 이론적 배경 및 통계적 추정치 등을 이용하여 공구 수명에 영향을 미치는 독립적 인자들을 선정해 모델을 구성하고 모델 예측 성능을 높이는 방법을 제시하였다.

3.1 회귀 인자 분석

다중 공선성이 있는 모든 인자들을 고려하여 회귀 모델을 적합한 후의 결과는 Table 2와 같다. 결정계수(R-squared) 값이 0.852로 비교적 높은 모델의 예측 성능을 확인할 수 있고, 인자들의 p value가 매우 낮아 유의미한 계수로 추정이 되지만, 회전수와 이송속도의 회귀 계수가 물리적인 관점에서 타당하지 않을 걸 확인할 수 있다. 두 변수는 강한 양의 상관관계를 갖고 있음에도 공구 수명에 회전수는 양의 방향으로 이송속도는 음의 방향으로 영향을 미치는 것으로 분석되어 모델의 예측 정확도를 신뢰하기 어렵다고 판단할 수 있다. 따라서 다중 공선성을 줄이고 예측 성능을 높이기 위한 회귀 모델을 구성하는 접근이 필요하다.

Table 2

Regression analysis results considering all factors

3.2 모델 선정

본 연구에서는 신뢰할 수 있는 모델을 구축하고자 인자들의 조합을 모두 고려하여 최적의 모델을 제안하였다. 공구 수명에 영향을 미치는 인자들의 모든 조합을 고려하여 회귀 모델을 적합하고 식(3)의 AIC (Akaike Information Criterion) 및 결정 계수 등을 고려하여 필요한 회귀 모델의 독립 변수를 선택하였다. AIC는 모델의 적합도(L)가 높아질수록 낮아지며, 모델의 복잡도(k)가 증가할수록 높아진다. 즉, AIC 값이 낮을수록 적합도는 높고 불필요한 변수가 적은, 더 간결한 모델이라는 것을 의미한다.

$\[ \begin{array}{c}\mathrm{A}\mathrm{I}\mathrm{C}=2\mathrm{k}-2\mathrm{l}\mathrm{n}\left(\mathrm{L}\right)\\ \left(\mathrm{k}:\mathrm{ }\mathrm{모}\mathrm{델}\mathrm{에}\mathrm{서}\mathrm{ }\mathrm{사}\mathrm{용}\mathrm{된}\mathrm{ }\mathrm{독}\mathrm{립}\mathrm{변}\mathrm{수}\mathrm{의}\mathrm{ }\mathrm{개}\mathrm{수}\right.\\ \left.\mathrm{L}:\mathrm{ }\mathrm{모}\mathrm{델}\mathrm{의}\mathrm{ }\mathrm{최}\mathrm{대}\mathrm{우}\mathrm{도}\left(\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{ }\mathrm{L}\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{d}\right)\right)\end{array} \]$

(3)

이를 통해 불필요한 변수를 제거하고, 가공 조건과 공구 수명 간의 관계를 가장 잘 설명하는 인자들 만을 포함한 모델을 구축하고자 하였다.

Table 3은 인자들의 수에 따른 모든 모델들을 회귀 적합 시키고 고려한 인자수에서 AIC 및 R-squared의 결과를 보여준다. R² 값은 모델이 종속 변수의 변동성을 얼마나 설명할 수 있는지를 나타내는 지표로 값이 1에 가까울수록 모델의 설명력이 높다는 것을 의미한다. Table 3에서도 변수 수가 증가하면서 설명력이 높아져 AIC가 낮아 지는 것을 볼 수 있고, 4개 이상의 인자를 고려하면 R-squared 값이 0.8보다 높아져 충분한 설명력을 갖는 모델이라고 볼 수 있다. 단순 AIC, R-squared 값 만을 가지고 평가하면 6개의 인자를 모두 고려한 모델(Model 1)이 최적의 모델로 평가할 수 있지만, 도메인 지식을 고려하면 앞에서 언급한 것처럼 공선성 문제로 모델의 설명력이 부족한 것으로 평가할 수 있다. 따라서 5개 인자를 고려한 모델 중 상호 상관계수가 높은 회전수와 이송 속도를 각각 제거한 모델을 평가하여 최적의 모델을 선정하였다. Tables 4와 5는 이송속도를 제외한 모델(Model 2)과 회전수를 제외한 모델(Model 3)의 회귀 적합 결과를 보여주며, 회전수에 비해 이송속도가 공구 수명을 예측하는데 중요한 변수라는 것을 보여준다.

Table 3

Optimal model according to number of factors

Table 4

Regression results excluding feed rate

Table 5

Regression results excluding spindle speed

4. 모델 검증

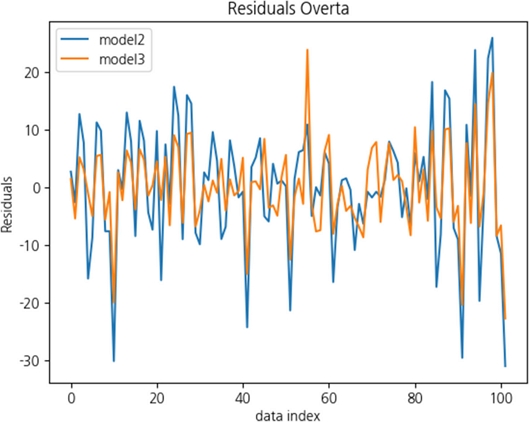
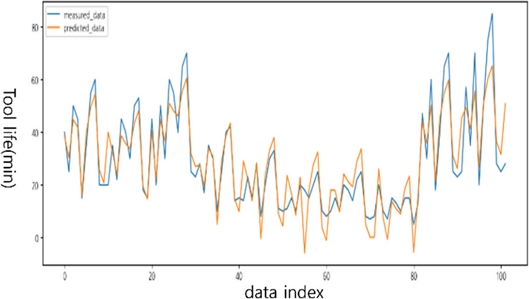
모든 인자를 고려한 모델은 통계적으로 높은 설명력을 보였으나, 도메인 지식에 기반하여 물리적 특성을 반영하지 못한다는 한계가 있었다. 따라서 상관계수가 높은 변수 중 하나만 고려하여 모델을 선정하였다. 최적 모델의 예측 결과는 실제 값과의 잔차를 Fig. 3에 그래프로 표현하였으며, 회전수를 제외한 모델인 Model 3이 가장 낮은 잔차를 나타냈다. 또한, Fig. 4에 나타낸 바와 같이 Model 3의 학습 데이터에 대한 예측값은 실제 데이터와 높은 일치도를 보였다. 이는 현장 데이터를 기반으로 한 회귀 모델이 제조 공정에서 실질적으로 활용될 가능성을 보여준다.

Fig. 3

Residuals of models 2 and 3

Fig. 4

Predicted values of model 3 vs. measured values

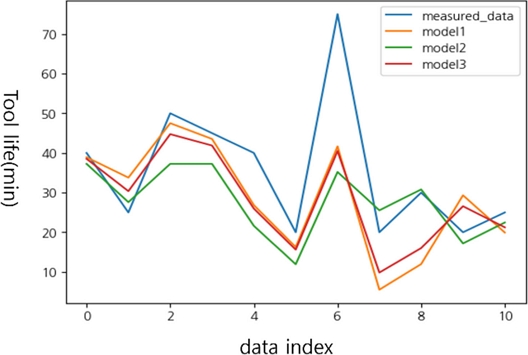
선정한 모델이 다른 모델에 비해 최적인지 평가하기 위해 검증 데이터를 활용한 모델 평가를 수행하였다. 학습에 사용되지 않은 11개의 검증 데이터에 대해 실제값과 모델의 예측값을 비교한 결과, Fig. 5에서 볼 수 있듯이 전체적으로 실제값을 잘 추종하는 경향을 보였다. 특히, Model 3은 평균제곱오차(MSE) 166.541, 평균절대오차(MAE) 9.3%로 가장 낮은 값을 기록하였다. Table 6은 각 모델의 예측 성능을 MSE, MAE, R-squared, RMSE 등 다양한 지표로 요약하여 보여준다.

Fig. 5

Predicted values vs. measured values

Table 6

Model evaluation results

앞에서 선정된 회전수를 제외한 5개의 인자로 구축한 최적화 모델은 검증 데이터 평가에서 가장 높은 예측 정확도를 나타냈다. 이는 모든 변수를 포함한 모델이 통계 지표상 바람직하게 보일 수 있으나, 도메인 지식을 활용해 핵심 변수를 선별함으로써 더 정확한 모델을 도출할 수 있음을 보여준다. 따라서 최적의 모델 구축을 위해 통계적 분석과 도메인 지식을 결합하는 접근이 필수적임을 확인하였다.

5. 결론

본 연구는 가공 조건에 따른 공구 수명을 예측하기 위한 회귀 모델을 개발하고, 이를 다양한 검증 방법으로 평가함으로써 제조 데이터 기반 예측 모델링의 실질적 가능성을 제시하였다. 주요 가공 조건인 절삭 속도, 이송 속도, 절입 깊이, 공구 회전수 등 핵심 인자들이 공구 수명에 미치는 영향을 정량적으로 분석하고, 도메인 지식과 통계적 방법을 결합한 변수 선택이 모델 성능 향상에 미치는 영향을 확인하였다.

특히, 모든 변수를 포함한 모델보다 일부 핵심 변수를 선별한 모델이 실제 검증 데이터에서 더 높은 예측 정확도를 보였다는 점은 본 연구의 주요한 차별성을 나타낸다. 이는 단순히 통계적 설명력에 의존하지 않고, 제조 공정의 물리적 특성을 반영한 변수 선택이 예측 성능과 실질적 활용 가능성을 높이는데 기여한다는 것을 시사한다.

또한, 교차 검증을 통해 모델의 일반화 성능을 확보함으로써 다양한 가공 조건에서도 신뢰성 있는 공구 수명 예측이 가능함을 입증하였다. 이러한 연구 결과는 공구 수명 예측 및 관리 시스템 개발에 기여할 수 있으며, 제조 현장에서 공구 수명을 최적화하고 생산성을 향상시키는데 직접적으로 활용될 수 있을 것이다.

향후 연구에서는 더 다양한 가공 조건과 공구 유형을 반영한 데이터 확장 및 고도화된 예측 기법을 도입하여, 보다 정교하고 포괄적인 예측 모델을 개발할 수 있을 것으로 기대된다.

Acknowledgments

이 논문은 2024년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(No. NRF-2021R1I1A3048752)과 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. RS-2024-00394769)

REFERENCES

• Li, W., Liu, T., (2019), Time varying and condition adaptive hidden markov model for tool wear state estimation and remaining useful life prediction in micro-milling, Mechanical Systems and Signal Processing, 131, 689-702. [https://doi.org/10.1016/j.ymssp.2019.06.021]
• Yang, M. Y., (1997), The Theory and Practice of Cutting Processing.
• Cook, N. H., (1973), Tool wear and tool life, Journal of Engineering for Industry, 95(4), 931-938. [https://doi.org/10.1115/1.3438271]
• Park, J.-J., (1990), Adaptive observer and computer vision for online flank wear estimation, University of Michigan.
• Lee, S.-H., Kim, B.-S., Kang, T.-H., Song, J.-Y., Kang, J.-H., Seo, C., (2004), Development of reliability prediction program for tool life, Proceedings of the KSMTE Spring Conference 2004, 317-322.
• Chen, Y., Jin, Y., Jiri, G., (2018), Predicting tool wear with multi-sensor data using deep belief networks, The International Journal of Advanced Manufacturing Technology, 99(5), 1917-1926. [https://doi.org/10.1007/s00170-018-2571-z]
• Sun, H., Cao, D., Zhao, Z., Kang, X., (2018), A hybrid approach to cutting tool remaining useful life prediction based on the wiener process, IEEE Transactions on Reliability, 67(3), 1294-1303. [https://doi.org/10.1109/TR.2018.2831256]
• Kim, B. S., Kang, T. H., Lee, S. H., Kang, J. H., Song, J. Y., (2005), Development of a tool life prediction program for increasing reliability of cutting tools, Transactions of the Korean Society of Machine Tool Engineers, 14(3), 1-7.
• Wang, M., Zhou, J., Gao, J., Li, Z., Li, E., (2020), Milling tool wear prediction method based on deep learning under variable working conditions, IEEE Access, 8, 140726-140735. [https://doi.org/10.1109/ACCESS.2020.3010378]
• Chen, Y., Jin, Y., Jiri, G., (2018), Predicting tool wear with multi-sensor data using deep belief networks, The International Journal of Advanced Manufacturing Technology, 99(5), 1917-1926. [https://doi.org/10.1007/s00170-018-2571-z]
• Liu, Y., Hu, X., Sun, S., (2019), Remaining useful life prediction of cutting tools based on support vector regression, IOP Conference Series: Materials Science and Engineering, 012021. [https://doi.org/10.1088/1757-899X/576/1/012021]