딥강화학습과 시뮬레이션을 활용한 제조 레이아웃의 물리적 배치 최적화

1. 서론

FLP (Facility Layout Problem)는 시설의 위치를 결정하는 최적화 문제로 주어진 지역 내에 여러 개의 시설을 어떻게 배치할지를 결정하는 데 중점을 둔다[1]. 이는 개별 공정과 장비의 배치 최적화, 작업자의 동선과 작업 공간 설계, 물류 이동 경로 최적화, 그리고 제조 레이아웃 최적화 등 여러 가지 문제를 포함한다. 초기 레이아웃 설계는 공정 흐름, 작업자 동선, 물류 이동 경로 등을 최적화하여, 공정의 생산성을 극대화하고 운영 비용을 절감하는 데 기여한다. 고품질의 레이아웃 솔루션은 불필요한 이동과 낭비를 최소화하고, 작업 환경을 개선하며, 전체적인 비용 절감 효과를 가져오기 때문에 FLP는 제조업에서 경쟁력을 강화하는 필수적인 요소로 인식되고 있다[2].

전통적인 FLP 방법은 선형 계획법, 유전 알고리즘과 같은 메타휴리스틱 기법 등이 주로 사용되었다[3-6]. 이러한 방식들은 특정 상황에서 효과적이나, 복잡하고 동적인 환경에서는 그 한계가 분명하다. 선형 계획법은 대규모 데이터의 처리에 제한적이며, 비선형 문제를 해결하기 어렵다[5]. 따라서 안전 거리, 장비의 크기, 장비의 회전 등을 모두 고려해야 하는 실제 상황에서 비효율적으로 적용될 수 있다. 메타휴리스틱 기법은 다양한 탐색 전략을 사용하지만, 무작위성을 기반으로 하여 최적화를 수행하기 때문에 해결 방안을 찾는 데 시간이 가변적이며, 항상 일정한 결과를 보장하지 않는다[7]. 복잡한 공정 흐름과 다양한 제약 조건을 고려해야 하는 FLP는 비선형성이 강하고, 문제의 규모가 커질수록 계산 시간과 복잡성이 기하급수적으로 증가한다. 이와 같은 이유로, 전통적인 접근법만으로는 현대 제조 환경의 복잡성을 충분히 다룰 수 없다는 한계를 지니고 있다.

이러한 한계점을 극복하기 위해 최근에는 강화학습(Reinforcement Learning)을 활용한 FLP 접근법이 주목받고 있다[8,9]. 강화학습은 에이전트가 환경과 상호작용하며 최적의 정책을 학습하는 방법으로, 최적화가 복잡하고 동적인 시스템에서 효과적인 방법으로 평가받고 있다. FLP 문제를 강화학습으로 해결하는 과정은, 주어진 시설 배치와 제약조건 하에서 에이전트가 각 시설의 위치를 선택하고 이동 경로를 결정하는 것으로 정의할 수 있다[9]. 이때 에이전트는 목표를 달성하기 위해 자원을 효율적으로 배분하고, 각 시설 간의 물류 흐름을 최적화하며, 주어진 시간 내에 최상의 레이아웃을 도출하는 것을 목표로 한다. 그러나 주로 사전에 정의된 설비를 최적의 위치에 배치하여 물류 효율성, 공간 활용성 등을 극대화하는 데 중점을 두고 있다[10-12].

따라서 본 논문에서는 DQN (Deep Q-Network)[13]을 활용하여 FLP 문제 중에서도 제조라인의 물리적 배치 최적화와 셀 생성 및 배치를 통합적으로 고려하는 접근법을 제안한다. 이를 통해 각 셀의 크기, 종류, 입력/출력 위치와 같은 물리적 제약 조건까지 반영하여 최적의 레이아웃을 도출하고자 한다. 특히, 다중 네트워크 구조를 활용하여 두 가지 과제를 동시에 해결하는 데 초점을 맞추고 있다. 첫 번째 과제는 제조라인 구성 요소를 배치하면서 공정 내의 불용공간과 겹치지 않도록 최적의 위치를 찾는 것이며, 두 번째 과제는 각 구성 요소에 적합한 셀의 크기와 종류를 결정하는 작업이다. 이 두 과제는 상호 연관된 문제로, 셀 배치의 공간적 제약과 특성을 반영하면서 전체 레이아웃을 최적화해야 한다. 본 연구는 이러한 다중 과제를 동시에 수행할 수 있는 접근법을 제안하며, 효율적이고 최적화된 제조 라인 배치를 도출하는 것을 목표로 한다.

이 두 과제는 각 단계에서의 의사결정이 이후 단계에 영향을 미치는 동적인 환경에서 진행되므로, 단순히 공간적 데이터를 학습하는 CNN (Convolutional Neural Network) 기반 접근법만으로는 해결하기 어렵다. 강화학습은 순차적 의사결정 문제를 효과적으로 처리할 수 있는 학습 능력을 제공하며, 셀 생성과 배치 작업의 상호작용을 반영하여 전체 레이아웃을 최적화할 수 있다. 본 연구는 이러한 강화학습의 장점을 활용하여 다중 과제를 동시에 수행하고, 효율적이며 최적화된 제조라인 배치를 도출하는 것을 목표로 한다.

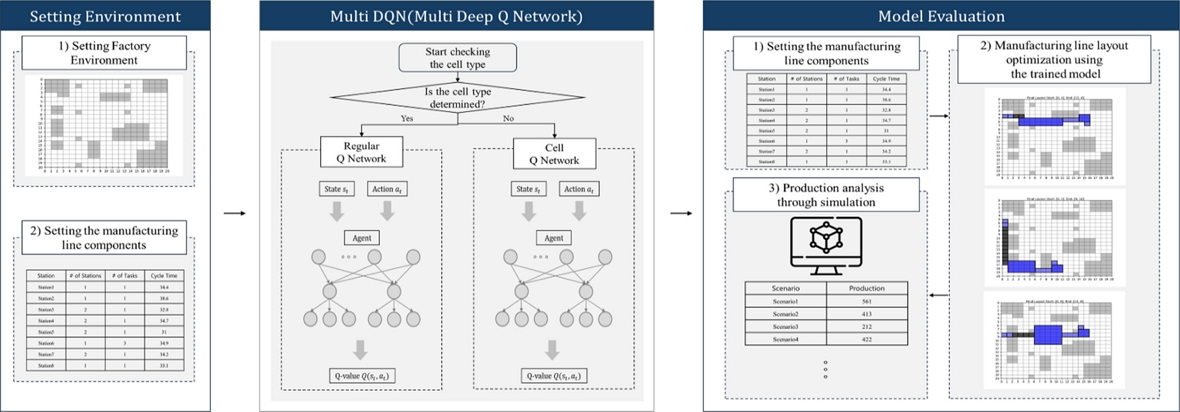
이후, 강화학습을 통해 도출된 제조라인 레이아웃의 유효성을 검증하기 위해 시뮬레이션을 활용한다. 이를 통해 학습 결과로 생성된 레이아웃의 생산량을 분석하며, 제안된 알고리즘의 실질적인 성능을 평가한다. 전체적인 흐름은 Fig. 1과 같다. 이러한 접근 방식은 기존의 전통적 방법론이 가지는 한계를 극복하고, 현대 제조 환경에서 적용 가능한 최적의 솔루션을 제시한다.

Fig. 1

Overall flowchart of proposed work

2. 관련 연구

2.2 강화학습과 DQN

강화학습은 에이전트가 환경과 상호작용하며 최적의 행동을 학습하는 기계 학습 기법이다. 에이전트는 주어진 상태에서 행동을 선택하고, 보상을 기반으로 정책을 개선하며 장기적인 보상을 극대화하기 위해 다양한 시나리오를 탐색한다. 주요 구성 요소는 상태(State), 행동(Action), 보상(Reward)으로, 상태는 환경의 현재 정보를 나타내고, 행동은 에이전트가 선택할 수 있는 옵션을, 보상은 행동 결과에 대한 피드백을 의미한다[12]. 이러한 구조는 복잡하고 동적인 환경에서도 효과적으로 작동하며, 게임, 로봇 제어, 자율주행 등 다양한 분야에서 성공적으로 활용되고 있다.

이 중 DQN은 Q-Learning[14]과 심층 신경망을 결합하여 복잡한 상태 공간에서도 최적의 행동 정책을 학습할 수 있는 강화학습 알고리즘이다[13]. 전통적인 Q-Learning의 메모리 및 계산 비용 문제를 해결하기 위해[15], DQN은 심층 신경망으로 상태를 입력 받아 Q값을 예측한다. 또한, 학습 안정성과 효율성을 높이기 위해 경험 리플레이를 활용하여 상관성을 줄이고 다양한 데이터를 학습하며, 타겟 네트워크를 통해 Q값의 변동을 완화해 안정적인 학습을 지원한다. DQN은 강화학습의 대표적인 알고리즘으로, 복잡한 환경에서의 효율적인 문제 해결에 널리 사용되고 있다[16].

2.2.1 Multi DQN (Multi Deep Q-Network)

본 연구에서는 제조라인 최적화 문제를 해결하기 위해 기존 DQN 구조를 확장하여 네트워크를 추가로 설계하였다. 이는 해당 문제가 단일 네트워크로는 다루기 어려운 복잡한 상태와 행동 공간을 포함하고, 두 가지 상호 연관된 과제를 동시에 해결해야 하기 위함이다. 기존 Q-Learning은 테이블 기반 접근법으로 대규모 상태 공간에서 비효율적이다[14]. 또한, 일반적인 DQN은 단일 네트워크 구조로 인해 여러 작업을 동시에 학습하려고 하면 네트워크의 학습 과정에서 충돌을 일으킬 수 있다. 본 연구에서는 각 과제에 맞는 독립적인 네트워크를 추가하여, 구성 요소의 배치와 셀 종류 결정을 병렬적으로 학습할 수 있도록 하였다. 이를 통해 각 과제의 특성을 효과적으로 반영하면서 제조라인 최적화 과정에서 발생하는 물리적 제약 조건과 상호작용을 동시에 고려할 수 있도록 하였다.

Multi-DQN 알고리즘은 제조 라인의 구성 요소를 배치하는 작업(Task)과 셀의 종류를 결정하는 작업이라는 두 가지 주요 작업을 학습하기 위해 설계되었다. 이를 위해 두 개의 별도 Q-네트워크(Regular Q-Network, Cell Q-Network)와 그에 상응하는 타겟 네트워크를 활용하여 각 작업에 맞는 상태와 행동 공간을 독립적으로 학습한다. Regular Q-Network는 구성 요소 배치를 위한 최적의 행동을 학습하며, Cell Q-Network는 각 셀의 종류를 결정하는 데 사용된다.

Algorithm 1

Multi DQN

해당 구조는 각 작업의 특성을 효과적으로 반영하면서도, 단일 네트워크로 해결할 수 없는 멀티태스킹 문제를 해결하도록 설계되었다. 각 Q-Network는 개별적인 Replay Buffer를 사용하여 학습되며, 특정 작업이 수행된 경우 해당 작업의 Replay Buffer만 업데이트된다. 즉, 타임스텝 t를 두 과제가 공유하며, 매 스텝마다 하나의 과제만 선택되어 실행된다. 또한, 현재 구조에서는 매 타임스텝마다 두 개의 Q-Network를 모두 업데이트하는 방식을 사용하여 특정 과제의 선택 빈도가 낮더라도 지속적인 학습이 이루어지도록 설계되었다. 또한, ε-탐욕 정책과 Kaiming He 초기화, 규제화를 통해 안정적이고 효율적인 학습을 지원한다[17].

3. 방법론

3.1 Multi DQN 학습

Multi DQN을 사용하여 제조라인의 물리적 배치 최적화에 관한 두 가지 과제를 동시에 학습하였다. 첫 번째 과제는 제조라인의 구성요소를 최적의 위치에 배치하는 과제이고, 두 번째 과제는 각 셀의 종류를 지정하는 과제이다. 각 과제는 서로 독립적으로 진행되지만, 동시에 학습하여 두 과제를 함께 해결할 수 있도록 설계되었다.

첫 번째 과제에서 에이전트의 목표는 각 구성요소를 배치할 때 불용공간을 최소화하고 구성요소가 서로 겹치지 않도록 최적의 위치를 선택하는 것이다. 두 번째 과제에서는 에이전트가 각 셀에 배치할 작업과 라인의 종류를 결정하여 전체적인 제조 라인의 효율성을 극대화하는 데 초점을 둔다.

학습은 환경의 각 시작점에서 10,000 번씩 수행되었으며, 불용공간과 겹치지 않는 배치를 찾는 목표를 두고 환경을 구성하였다. 이 과정에서 각 과제의 상호작용을 고려하여 두 가지 과제를 동시에 최적화하는 방법을 학습하였다. 학습 과정에서는 Table 1에 정리된 알고리즘의 주요 하이퍼파라미터를 사용하였다. 또한, 학습 과정에서 사용하는 네트워크의 구조는 Table 2에 나타나 있다. 해당 모델은 입력 데이터의 차원을 줄이고 주요 특징을 추출하기 위해 Fully Connected 레이어와 Dropout을 결합하여 구성하였다. fc3 레이어의 경우에는 각 과제의 행동 차원에 따라 Output이 달라지게 된다.

Table 1

Parameters in algorithm 1

Table 2

Architecture of algorithm 1

3.1.1 데이터셋

제조라인의 각 스테이션에 대한 정보는 중요한 데이터로 활용되며, Table 3은 각 스테이션의 번호, 스테이션의 개수(# of Stations), 작업 수(# of Tasks), 그리고 사이클 타임(Cycle Time)을 포함하고 있다. 예를 들어, Stations 1, 2, 6, 8은 각각 1개의 스테이션으로 구성되어 있으며, 이를 1 × 1 크기의 스테이션으로 지정할 수 있다. 반면, 스테이션의 개수가 2개 이상인 다른 스테이션들은 동일한 개수를 가진 스테이션 번호들과 함께 하나의 Cell로 지정할 수 있다.

Table 3

Manufacturing line data

이러한 데이터를 기반으로, 스테이션 개수가 2개 이상인 경우에는 하나의 Cell로 통합될 수 있다. 이때 에이전트는 4가지 Cell 유형 중 하나를 선택하는 두 번째 과제를 수행한다. 이는 각 Cell 유형이 가지는 특성에 따라 공간 효율성과 작업 흐름이 달라지기 때문에, 에이전트는 최적의 Cell 유형을 선택하여 제조라인의 효율성을 극대화하도록 학습된다. 반면, 스테이션 개수가 1개이거나 이미 Cell의 종류가 지정된 경우에는 해당 구성 요소를 불용공간과 겹치지 않도록 배치하는 과제 첫 번째 과제를 수행한다. 이 과정에서 불용공간과의 겹침을 피하며 최적의 배치를 찾아내는 것이 핵심이다.

3.1.2 환경(Environment) 설정

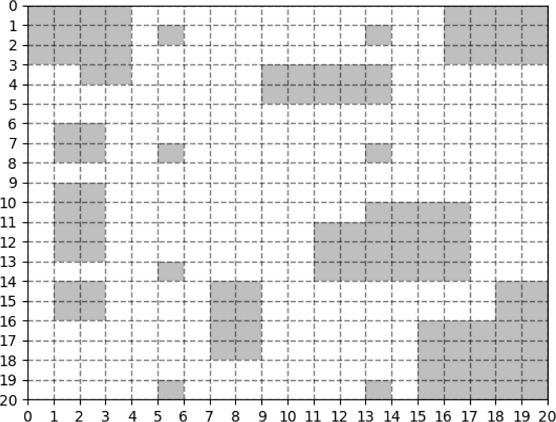
공정 내부의 크기는 20 × 20 크기의 격자(Grid)로 설정하였다. Fig. 2는 해당 격자 내에서 기둥, 계단과 같은 불용공간에 대한 정보를 입력 받아 회색으로 시각화한 결과이며 흰색으로 표시된 공간은 가용공간을 나타낸다.

Fig. 2

Factory environment

3.1.3 상태(State) 설정

강화학습에서 상태는 에이전트가 특정 시점에서 환경을 인식하고 표현하는 정보를 의미한다. 해당 알고리즘에서는 두 가지 과제에 대한 상태를 각각 다음과 같은 벡터 형태로 나타낸다:

1) 제조라인의 구성요소 배치 시: [x, y, w, h]

• • 현재 위치(x, y): 에이전트의 현재 위치를 좌표 형태로 나타낸다.
• • 다음 에이전트 크기(w, h): 다음으로 배치해야 할 제조라인 구성요소의 크기를 나타낸다.

2) 셀 종류 결정 시: [x, y, t, l]

• • 현재 위치(x, y): 에이전트의 현재 위치를 좌표 형태로 나타낸다.
• • Task 개수(t): 각 셀에 배치할 작업의 수를 나타내며 Table 3의 # of Tasks 항목과 대응된다.
• • Line 개수(l): 각 셀에 배치된 라인의 개수를 나타내며 Table 3의 # of Stations 항목과 대응된다.

학습 시 초기 좌표 값은 환경 초기화 시 기본값인 (0,3)으로 설정되며 임의의 시작점 지정도 가능하다. 평가 시에는 특정 시작점을 입력하면 해당 시작점에서의 최적의 배치 결과를 도출한다. 좌표값은 에이전트의 위치를 나타내며 이는 현재 제조라인 구성요소가 어디에 위치하고 있는지를 나타낸다.

본 연구에서는 불필요한 데이터 처리를 줄이고 효율적인 학습을 유도하기 위해 과거 배치된 구성요소의 정보를 포함하지 않고 현재 상태에서 최적의 행동을 학습하도록 설계하였다. 에이전트는 불용공간 즉, 장애물의 위치와 이미 지나온 위치에 구성요소를 배치할 경우 지속적으로 음의 보상을 받도록 되어 있어, 자연스럽게 올바른 배치를 학습하게 된다. 또한, 셀 종류 결정 시 상태 벡터에 포함되는 Line 개수(l)은 해당 Cell을 구성하는 Station 개수와 동일한 값으로 지정된다. 이는 주어진 Station 개수만큼 병렬로 Cell을 구성하기 때문에 Line 개수는 자동으로 해당 Station 개수와 일치하도록 설정된다. 이와 같은 상태 정의를 통해 에이전트가 현재 환경과 다음 행동을 위한 정보를 학습할 수 있도록 한다.

3.1.4 행동(Action) 설정

강화학습 환경에서 에이전트는 주어진 과제를 달성하기 위해 다양한 행동을 수행하며 학습을 진행한다. 각 행동은 에이전트가 환경 내에서 상호작용하며 목표를 이루기 위한 선택지로 정의된다. 본 연구에서는 제조라인 구성요소 배치와 셀 종류 지정이라는 두 가지 과제에 대해 서로 다른 행동을 정수형 스칼라 값으로 설정하였다.

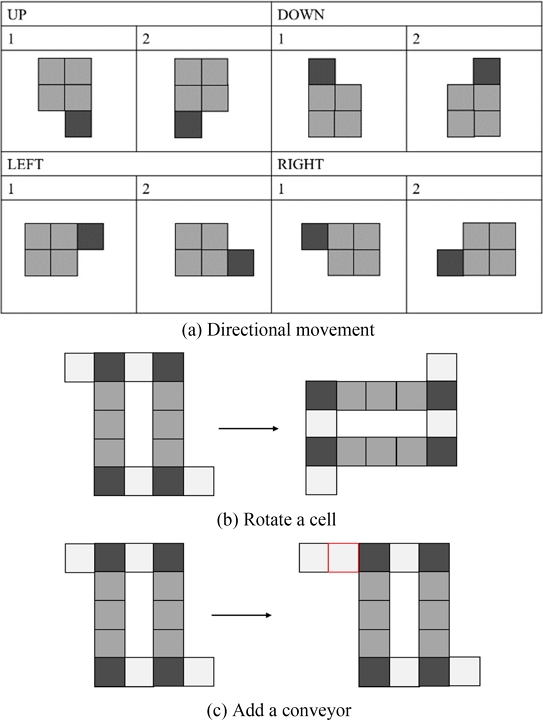
첫 번째 과제인 제조라인 구성요소 배치 과제에서는 에이전트가 다양한 위치와 방향으로 이동하거나 구성요소의 속성을 조정하는 행동을 수행해야 한다. 이 과제에서는 총 10가지 행동(0-9)이 정의되며, 이는 항상 일정하게 유지된다. 8가지 행동은 Fig. 3(a)에 나타난 상, 하, 좌, 우 이동 로직에 기반하며, 이는 에이전트가 제조 라인의 구성요소를 적절히 배치할 위치를 탐색하도록 돕는다. 추가적으로, Figs. 3(b)의 현재 Cell을 90^o 회전시키는 행동과 3(c)에 나타난 1 × 1의 Conveyor를 추가하는 행동도 포함한다. Fig. 3(c)에서는 개념적인 이해를 돕기 위해 임의로 추가한 Conveyor를 오른쪽에 배치하였지만 이는 단순히 1 × 1 크기의 구성요소를 추가하는 방식으로 적용된다. 추가된 Conveyor는 새로운 구성 요소로 간주되며, 이후 타임 스텝에서도 동일하게 10가지 행동 중 하나를 선택하여 수행된다. 이러한 행동 설정은 주어진 환경에서 가능한 최적의 배치 방법을 최대한 많이 찾기 위함이다.

Fig. 3

Action system for task 1

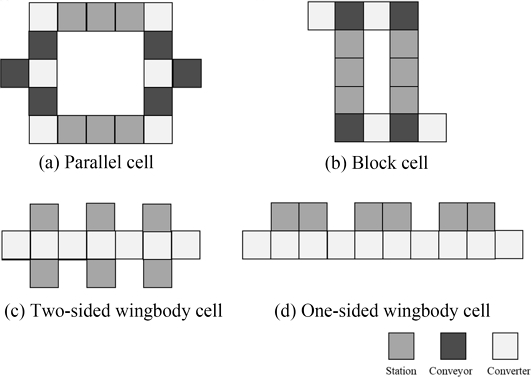
두 번째 과제인 셀의 종류 지정 과제에서는 Fig. 4와 같이 에이전트가 선택할 수 있는 4가지 행동(0-3)이 존재한다. 제조라인에서의 Cell은 Parallel Cell, Block Cell, Two-sided Wingbody Cell, One-sided Wingbody Cell로 분류한다[20]. 이는 각 셀을 미리 정의된 유형 중 하나로 지정하는 선택지를 의미한다. 셀의 크기는 작업(Task) 수와 라인(Line) 개수에 따라 결정되며, 에이전트는 해당 정보를 기반으로 적합한 셀 유형을 선택하는 행동을 수행한다.

Fig. 4

Action system for task 2

3.1.5 보상(Reward) 설정

본 연구에서는 첫 번째 과제와 두 번째 과제 그리고 에피소드 종료 시점에서의 보상 체계를 설계하여 에이전트가 효율적으로 학습할 수 있도록 유도하였다.

첫 번째 과제의 보상 체계 r_r는 식(1)과 같이 다음 두 가지 조건으로 구성된다.

$\[ {\mathbf{r}}_r=\left\{\begin{array}{c}-5\mathrm{*}{\mathrm{n}}_{\text{restricted}},\text{Overlap with restircted area}\hfill \\ -10,\text{Conveyor added or cell rotated}\hfill \\ -10,\text{Occurrences of Turns}\hfill \end{array}\right. \]$

(1)

• • 불용공간과 겹치는 경우: 장애물 또는 기존 배치와 겹치는 칸 수에 비례하여 음의 보상 부여
• • 컨베이어가 추가되거나 셀의 회전이 일어난 경우: 추가 작업으로 인한 비효율성을 억제하기 위해 음의 보상 부여
• • 꺾임 발생: Directional Movement 중 이전 행동과 달라졌다면 음의 보상 부여

해당 체계는 제조라인 배치를 최적화하고 자원을 효율적으로 활용하기 위해 설계되었다. 이를 통해 에이전트는 불필요한 구성요소 추가 또는 회전을 줄이고, 제한된 공간 내에서 최적의 배치를 학습할 수 있다.

적절한 셀의 종류를 결정하는 두 번째 과제의 보상 체계 r_c는 다음 식(2)와 같다.

$\[ {\mathbf{r}}_c=\left\{\begin{array}{cc} +10,\hfill & \text{if valid move exist}\hfill \\ -10,\hfill & \text{if no valid moves}\hfill \end{array}\right. \]$

(2)

• • 유효한 이동 체계가 존재하는 셀의 종류를 선택한 경우: 선택한 셀이 이동가능한 구조를 가진 경우 즉, 선택한 셀에서 유효한 Directional Movement가 존재한다면 양의 보상 부여
• • 유효한 이동 체계가 존재하지 않는 셀의 종류를 선택한 경우: 선택한 셀에서 유효한 이동 체계가 존재하지 않을 경우, 즉, 선택한 셀에서 유효한 Directional Movement가 존재하지 않는다면 음의 보상 부여

이 보상 체계는 에이전트가 유효한 이동 체계를 가진 셀을 선택하도록 학습하고, 비효율적인 선택을 최소화하는 방향으로 최적화를 진행할 수 있도록 설계되었다.

마지막으로, 에피소드 종료 조건은 크게 2가지로 구분되며 이에 대한 보상 체계 r_t는 두 개의 과제에 동일하게 식(3)으로 적용된다.

$\[ {\mathbf{r}}_t=\left\{\begin{array}{c}-100\times {\mathrm{n}}_{\text{unplaced}},\text{Episode ends }: \text{Placement failure}\hfill \\ 100,\text{Episode ends }: \text{Placement success}\hfill \end{array}\right. \]$

(3)

• • 배치 실패로 에피소드가 종료된 경우: 배치하지 못한 구성요소의 수에 비례하여 음의 보상 부여
• • 배치 성공으로 에피소드가 종료된 경우: 높은 기본 보상 제공

첫 번째 과제 수행 중 특정 위치에서 수행할 수 있는 모든 행동이 불가능한 경우, 배치 실패로 간주하여 에피소드를 종료한다. 이는 Fig. 3에서 정의된 모든 이동 방식 및 Cell 회전이 불용 공간과 충돌하거나, Conveyor 추가 개수가 10개를 초과하여 더 이상 배치가 불가능한 상황을 의미한다. 반면, 모든 구성 요소가 정상적으로 환경 내에 배치 완료된 경우, 해당 에피소드는 성공적으로 종료된다. 이를 통해 불필요한 추가 행동을 방지하고, 최적의 배치를 신속하게 학습할 수 있도록 설계하였다.

총 보상 계산은 아래의 식(4)와 같다.

$\[ Total Reward=\left\{\begin{array}{c}{\mathrm{r}}_{\mathrm{t}}\text{ if done}=\text{True}\\ {\mathrm{r}}_{\mathrm{r}},\text{if task }1\\ {\mathrm{r}}_{\mathrm{c}},\text{if task }2\end{array}\right. \]$

(4)

해당 보상 체계는 에이전트가 각 과제의 목표를 효과적으로 달성할 수 있도록 설계되었으며, 배치 실패를 줄이고 효율적인 셀 선택과 배치를 학습하도록 유도한다.

4. 실험 결과

4.1 Multi DQN 학습 결과

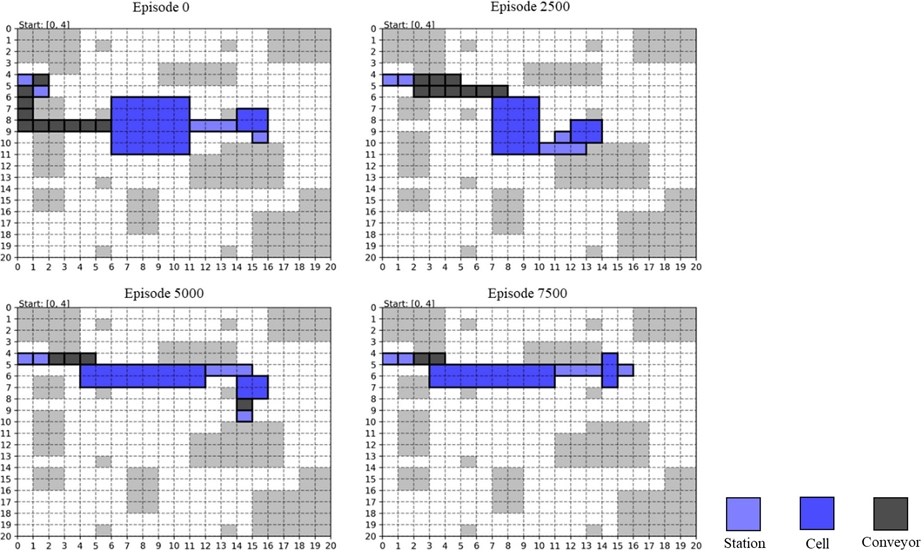
본 연구에서는 20 × 20 크기의 그리드 환경을 구성하여, 불용공간을 제외한 각 시작점에서 10,000번의 에피소드를 학습하였다. 강화학습의 유효성을 평가하기 위해 1,000번마다의 성공한 에피소드 개수와 시작점(0, 4)에서 약 0, 2,500, 5,000, 7,500번 에피소드일 때의 배치 결과를 시각화 하여 분석하였다(Fig. 5).

Fig. 5

Learning process at the starting point(0, 4)

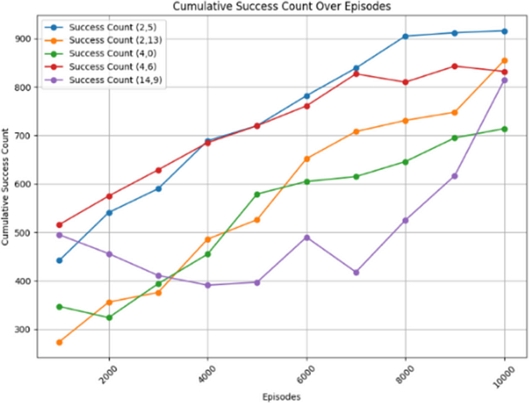
Fig. 6에 따르면 각 시작점에서의 성공적인 에피소드 수는 시간이 지남에 따라 점진적으로 증가하는 추세를 보인다. 이는 모델이 초기에는 랜덤한 경로를 탐색하면서 비교적 낮은 성공률을 보였으나, 점차 최적의 경로를 학습함에 따라 성공률이 꾸준히 개선되었음을 보여준다. 특히, 에피소드 7,500 이후에는 대부분의 경우에서 성공 수가 800-900 사이로 수렴하며 안정적인 성과를 보인다.

Fig. 6

Cumulative success count over episodes

Fig. 5에서 확인할 수 있듯이, 에피소드 0에서는 경로가 불규칙하고 불필요한 Conveyor가 추가된 것을 확인할 수 있다. 그러나 학습이 진행됨에 따라 경로가 점차 단순화되고 최단 경로로 수렴하는 양상을 보인다. 최종적으로 에피소드 7,500에서는 거의 최적의 경로가 도출되어, 불필요한 Conveyor 추가나 꺾임 없이 적절한 배치가 이루어졌다. 따라서, Multi-DQN 모델이 학습 과정을 통해 제조라인 경로 탐색 문제를 효율적으로 해결하며, 안정적으로 최단 경로를 학습하였음을 확인하였다.

4.2 시뮬레이션 기반 검증

강화학습 이후 최적화된 제조라인의 각 요소 정보를 저장한 다음, 이를 기반으로 시뮬레이션을 통해 생산량 분석을 진행하였다. 제조라인 각 요소의 사이클 타임을 기준으로 총 6시간의 전체 생산량을 도출하였다. 불용공간을 제외한 모든 시작점에서 학습한 후, 시뮬레이션을 통해 각 시나리오의 생산량을 분석하였다. 분석 결과, 해당 데이터셋은 Cycle Time이 긴 Station들이 강화학습 단계에서 병렬 Cell로 배치되어 작업이 동시에 이루어질 수 있도록 설계되었기 때문에 생산량 관점에서 유효한 차이가 나타나지 않았다. 따라서 Table 4와 같이 모든 최종 시나리오 결과를 바탕으로 경로의 꺾임 횟수와 추가된 Conveyor 개수, 공간 차지율을 함께 분석하여 추가적인 효율성 평가를 수행하였다.

Table 4

Indicator analysis

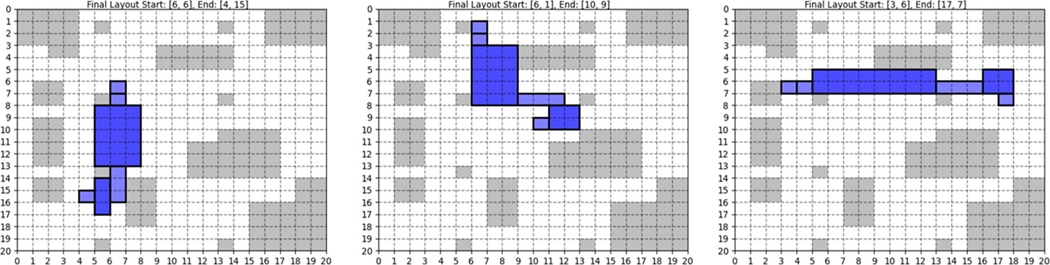
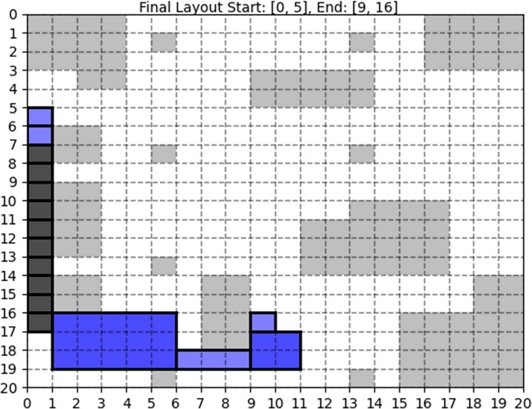
네 가지 관점에서의 상위 3가지 시나리오를 Fig. 7에 나타냈다. 이러한 시나리오에서는 경로 복잡성이 낮고 꺾임 횟수가 적으며, 최소화된 Conveyor 추가가 특징이다. 도출된 최적의 시나리오 중 가장 비효율적이라고 판단한 시나리오는 Fig. 8이다. 생산량 측면에서는 큰 차이가 없었지만 추가된 Conveyor 개수가 10개로 공간 차지율이 가장 높게 나타났다.

Fig. 7

The top three scenarios

Fig. 8

Most inefficient layout

5. 결론

본 연구에서는 강화학습과 시뮬레이션을 활용하여 셀 종류 최적화와 제조라인의 배치 최적화를 시도하였다. 강화학습은 레이아웃 설계에서 공간 활용성과 물리적 경로의 효율성을 극대화하는 데 중점을 두었으며, 시뮬레이션은 실제 제조 환경에서 다양한 제약 조건과 물리적 제약을 반영한 결과를 제공하였다. 이를 통해 복잡한 제조 환경에서도 실질적인 성능을 보장할 수 있는 레이아웃을 설계하였다.

다만, 본 연구에서는 강화학습 모델이 특정 환경에 맞춰 학습되었기 때문에, 환경이 바뀔 경우 다시 수행해야 하는 일반화 성능의 한계가 존재한다. 이를 해결하기 위해 향후 연구에서는 매 에피소드마다 다른 환경을 입력하거나, Dense Block을 사용하여 네트워크의 표현력을 향상시키는 방법, 또는 환경에 대한 사전 학습을 먼저 진행하는 방법을 고려하고자 한다. 추가로 특정 데이터셋을 기반으로 모델 학습을 진행했기 때문에 두 과제 간 데이터 불균형 문제가 두드러지지 않았다. 향후 더 다양한 데이터셋을 활용한 학습을 진행할 경우, 과제 간 선택 빈도를 조정하거나 Q-Network의 업데이트 방식을 개선하는 방안을 고려할 예정이다.

본 연구에서는 강화학습과 시뮬레이션이 별도로 수행되었기 때문에, 두 프로세스 간의 실시간 상호작용이 제한적이다. 향후 연구에서는 강화학습과 시뮬레이션을 실시간으로 통합하여 단일 프레임워크 내에서 물리적 최적화와 논리적 최적화를 동시에 달성하는 방법론을 제안할 예정이다. 강화학습의 보상 체계는 시뮬레이션 결과를 즉각 반영하여, 공간 활용성과 물류 경로 최적화 뿐만 아니라, 제조 공정의 실제 성능까지 포함하는 다각적 관점에서의 최적화가 가능하도록 설계할 예정이다.

Acknowledgments

이 연구는 서울과학기술대학교 교내연구비의 지원으로 수행되었습니다.

REFERENCES

• Pérez-Gosende, P., Mula, J., Díaz-Madroñero, M., (2021), Facility layout planning, An extended literature review, International Journal of Production Research, 59(12), 3777-3816. [https://doi.org/10.1080/00207543.2021.1897176]
• Drira, A., Pierreval, H., Hajri-Gabouj, S., (2007), Facility layout problems: A survey, Annual reviews in control, 31(2), 255-267. [https://doi.org/10.1016/j.arcontrol.2007.04.001]
• Steinbrunn, M., Moerkotte, G., Kemper, A., (1997), Heuristic and randomized optimization for the join ordering problem, The VLDB journal, 6, 191-208. [https://doi.org/10.1007/s007780050040]
• Singh, S. P., Sharma, R. R., (2006), A review of different approaches to the facility layout problems, The International Journal of Advanced Manufacturing Technology, 30, 425-433. [https://doi.org/10.1007/s00170-005-0087-9]
• Luenberger, D. G., Ye, Y., (1984), Linear and nonlinear programming, Springer.
• Nordin, N. N., Lee, L. S., (2016), Heuristics and metaheuristics approaches for facility layout problems: A survey, Pertanika Journal of Scholarly Research Reviews, 2(3), 62-76.
• Yang, X.-S., (2011), Metaheuristic optimization: Algorithm analysis and open problems, International Symposium on Experimental Algorithms, 21-32. [https://doi.org/10.1007/978-3-642-20662-7_2]
• Ikeda, H., Nakagawa, H., Tsuchiya, T., (2022), Towards automatic facility layout design using reinforcement learning, FedCSIS (Communication Papers), 11-20. [https://doi.org/10.15439/2022F25]
• del Real Torres, A., Andreiana, D. S., Ojeda Roldán, Á., Hernández Bustos, A., Acevedo Galicia, L. E., (2022), A review of deep reinforcement learning approaches for smart manufacturing in industry 4.0 and 5.0 framework, Applied Sciences, 12(23), 12377. [https://doi.org/10.3390/app122312377]
• Lee, S. H., Ji, S. Y., (2021), Development of an AI-based spatial arrangement simulator using reinforcement learning, Journal of the Architectural Institute of Korea, 37(11), 43-53.
• Choi, H., Yu, S., Lee, D., Noh, S. D., Ji, S., Kim, H., Han, J., (2024), Optimization of the factory layout and production flow using production-simulation-based reinforcement learning, Machines, 12(6), 390. [https://doi.org/10.3390/machines12060390]
• Klar, M., Schworm, P., Wu, X., Simon, P., Glatt, M., Ravani, B., Aurich, J. C., (2024), Transferable multi-objective factory layout planning using simulation-based deep reinforcement learning, Journal of Manufacturing Systems, 74, 487-511. [https://doi.org/10.1016/j.jmsy.2024.04.007]
• Mnih, V., (2013), Playing atari with deep reinforcement learning, arXiv:1312.5602, .
• Sutton, R. S., Barto, A. G., (2018), Reinforcement learning: An introduction, MIT Press.
• Watkins, C. J., Dayan, P., (1992), Q-learning, Machine Learning, 8, 279-292. [https://doi.org/10.1023/A:1022676722315]
• Arulkumaran, K., Deisenroth, M. P., Brundage, M., Bharath, A. A., (2017), Deep reinforcement learning: A brief survey, IEEE Signal Processing Magazine, 34(6), 26-38. [https://doi.org/10.1109/MSP.2017.2743240]
• Farebrother, J., Machado, M. C., Bowling, M., (2018), Generalization and regularization in dqn, arXiv:1810.00123, .
• Zeigler, B. P., Muzy, A., Kofman, E., (2018), Theory of modeling and simulation: Discrete event & iterative system computational foundations, Academic Press.
• Van Tendeloo, Y., Vangheluwe, H., (2015), Pythonpdevs: A distributed parallel devs simulator, Proceedings of the Symposium on Theory of Modeling & Simulation: DEVS Integrative M&S Symposium, 91-98.
• Choi, S. H., Kim, B. S., (2024), Intelligent factory layout design framework through collaboration between optimization, simulation, and digital twin, Journal of Intelligent Manufacturing, 1-15. [https://doi.org/10.1007/s10845-024-02340-3]