Enhancing Chatter Vibration Analysis in Turning Processes through Advanced Multiple-denoising Wavelet Techniques
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study investigated the natural frequency of a self-excited vibrating workpiece and cutting tool using a hammer impact test to acquire vibration data. Time-domain cutting vibration data were converted to the frequency domain using FFT. The workpiece signal exhibited a high amplitude, peaking at 392 Hz, while the cutting tool signal presented a peak at 930 Hz. Stability Lobe Diagrams were constructed to assess dynamic stability. Cutting experiments revealed an obvious relationship between spindle speed and signal amplitude, with higher speeds leading to larger amplitudes. Frequency analysis revealed a peak near the cutting tool's 900 Hz natural frequency. Smoother surface finishes were observed at 0.15 mm cutting depth, while 0.2 mm resulted in a wavy surface, indicating chatter. To investigate chatter frequency and reduce noise, a multiple-denoising method combined Bior 3.7 and DB10 wavelets to reduce amplitude and improve signal representation, especially for non-smooth features. The proposed method aimed to reduce the 900 Hz cutting tool’s natural frequency. Results showed a clear chatter frequency at 450-480 Hz for 0.2 mm depth cuts at spindle speeds of 500, 1,000, and 1,400 rpm. The proposed method exhibited high efficiency, achieving the higher signal-to-noise ratio and lower mean-square error than Bior 3.7 and DB10 wavelet denoising techniques.
Keywords:
Chatter frequency, Cutting force and tool interaction vibration, DWT wave transform, Multiple-denoising method, Stability lobe diagram (SLD)1. Introduction
The turning process is operated on a lathe using a single-point cutting tool. The cutting parameters, tool geometry, workpiece qualities, cutting tool-workpiece interaction, and machine tool vibration all affect the quality of the machined surface and the cutting force [1]. The occurrence of relative vibration may be due to the cutting force exerted between the tool and the workpiece. The mechanical vibration that occurs during the turning process may be categorized into three types, including free vibration, force vibration, and self-excited vibration [2]. Free vibration caused by impulsive loading has a transient effect on the elastic structure of a machine, tool. Force vibration is generated by periodic forces, for instance, due to spindle instability, gear system flats, and periodic chip breaking on the Build-Up-Edge (BUE) formation of a cutting tool. Self-excited vibration is caused by high cutting power operating on the flexibility or low dynamic stiffness of the machine tool structure. The occurrence of self-excited vibration may be attributed to the application of high cutting power, which acts upon the flexibility or poor dynamic stiffness of the structure of the machine tool [3]. Chatter is a self-excited, unstable vibration phenomenon characterized by violent relative motion between the workpiece and cutting tool. This phenomenon typically occurs near the natural frequencies of the tool-workpiece system, resulting in amplified and dynamically varying cutting forces at a critical depth of cut [4]. The occurrence of waviness on machined surfaces may be due to the excitation and vibration phenomena by the machine tool and workpiece system. Chatter vibration has a significant impact on the useful life of tools, the quality of surfaces, and the efficiency of machining processes [2]. Therefore, it is essential to use chatter detection technologies to maintain machining quality in the turning process. The vibration of a machining process is influenced by several factors, including cutting speed, feed rate, spindle speed, depth of cut, tool stiffness, and machine stiffness. It is therefore crucial that monitoring techniques are used in the machining process to effectively reduce chatter vibrations. Vibration sensors were used to monitor several types of vibration signals in the turning process, including measurement noise, machine tool vibration, and chatter vibration. The detected signals were analyzed for vibrations using signal processing analysis techniques such as Fast Fourier Transform (FFT) and Short-time Fourier Transform (STFT) [5,6]. However, the FFT is incapable of analyzing the vibrating frequency and chatter vibration [5] because it averages the frequency composition across the length of the signal with a fixed resolution over the whole frequency range. Nevertheless, the FFT may not consistently provide satisfactory outcomes when applied to nonstationary vibration signals [7]. Additional signal processing techniques, such as the STFT and Wavelet Transforms (WT), may also be used for analytical purposes [8]. The STFT is primarily used to analyze data in the time and frequency domains, particularly in cases where excellent resolution is desired. One such approach is STFT, which allows for the extraction of frequency components within certain time periods of a predetermined length [9]. However, to examine signals that exhibit non-periodic and rapid transient characteristics, the use of WT becomes necessary [8]. At high frequencies, it offers excellent time resolution but exhibits inadequate frequency resolution. Conversely, at low frequencies, it has satisfactory frequency resolution but offers limited time resolution. The wavelet transform has significant advantages when used to examine transient signals.
WT have been increasingly used in the analysis of vibrations during cutting processes in recent years. There are two distinct kinds of wavelet transforms including continuous wavelet transform (CWT) and discrete wavelet transform (DWT) [8]. DWT is a widely used technique for efficiently decorrelating obtained data. This is achieved by dividing the data into two subsequences, each with a reduced sampling rate, while preserving the relevant information [10]. A robust signal processing methodology was used to recover the frequency of chatter from signals contaminated with noise [11]. During experimental procedures, it is customary to capture oscillatory signals as well as other forms of vibration and ambient noise. Elimination of these disturbances from the vibration signal may be achieved exclusively using wavelet denoising techniques [12]. Different families of wavelets, including Haar, Daubechies, and Biorthogonal, among others, were used to denoise the signal. Wavelets were used to denoise chatter vibration in turning. The constructed nonstationary wavelets were compared to the classical Daubechies biorthogonal wavelet family, and the nonstationary wavelets were found to be dominant in approximating different kinds of signals [4,13]. In the context of chatter detection in turning, a dual-mode type algorithm was proposed using wavelet packet entropy as the chatter detection indicator [5]. The algorithm was able to detect chatter vibration even when the measured signal possessed beat characteristics [6]. However, there is no mention of specific wavelet types, such as Haar, Daubechies, or Biorthogonal, being used for denoising chatter vibration in turning.
The development of an accurate and efficient method for early identification and suppression of chatter vibration in turning operations is necessary. New investigation techniques can be used to explore the effectiveness of the proposed dual-mode type algorithm for chatter detection in the turning process. The algorithm can be refined and optimized to improve its accuracy and efficiency in detecting chatter vibrations, especially in the presence of vibration phenomena. Additional research could be conducted to verify the effectiveness of the established chatter detection method across various cutting settings, including different cutting speeds, feed rates, and depths of cut [14]. The development of an algorithm aimed at improving the analytical approach for chatter detection, specifically focusing on cutting parameters, was considered necessary.
To effectively address the problem of excessive noise, the optimization cutting parameters, such as the depth of cut and rotating speed, must be considered. Natural frequency experiments consist of force vibration, free vibration and chatter vibration or self-excited vibration to identify the cutting system's inherent frequency [15,16]. The vibration frequency during free cutting or spindle rotation as well as the natural frequency of the machine spindle speed were measured to determine the force vibration. The free vibration was determined from the natural frequency cutting tool holder. The natural frequency of the self-excited oscillator was obtained by using the vibration sensor to measure vibration generated by the cutting process. The Stability Lobe Diagram (SLD), which is derived from the natural frequency of the workpiece, is a numerical simulation output that presents the relationship between the axial depth of the cut and the rotational speed of the spindle [17,18]. Stable and unstable areas in which non-chattering and chattering vibrations occur throughout the turning process are shown in the SLD graph [19]. To mitigate the effects of chatter vibration, the most suitable depth of cut for every rotation speed of the spindle should be selected from the SLD graph. The occurrence of vibrations takes place inside the instability zone of the SLD graph, which is subject to the effect of both free and forced vibration. This approach leads to a waviness pattern on the final product surface [20].
Achieving optimal machining conditions necessitates minimizing this vibration and the associated chip frequency. While sensorbased chatter detection is prevalent, measured signals are often corrupted by background noise and other disturbances. Therefore, effective denoising techniques are crucial. As mentioned above, a new method to analyze the signal in turning chatter by using DWT is required. Validation of the optimized cutting parameters on the SLD graph necessitated performing an empirical examination of chatter vibration for each individual machine tool. The objective of the present study was to use the multi-denoise wavelet family of DWT to analyze the frequencies of chatter vibration and eliminate both free and forced vibration in the turning process, specifically at the critical depth of cut. To propose a method for multipledenoising with DWT to reduce the frequencies of vibration in the turning process and determine the chatter vibration.
2. Materials and Methods
2.1 Workpiece and Cutting Tool Preparation
The material was St37 carbon steel 25 mm in diameter and 165 mm long. As shown in Fig. 1, the workpiece was clamped in three jaws on the lathe at a distance of 20 and 145 mm from the edge of the jaws. The cutting tool employed coated CVD TiCN, Al203, and TiN with a clearance angle of 0 degrees and 0.397 mm. The recommended depth of cut for this cutting tool is in the range of 0.15-2.0 mm. The tool holder was 125 mm long with a clearance angle of 95 degrees and a cutting edge length of 12 mm.
2.2 Numerical Model and Stability Lobe Diagram
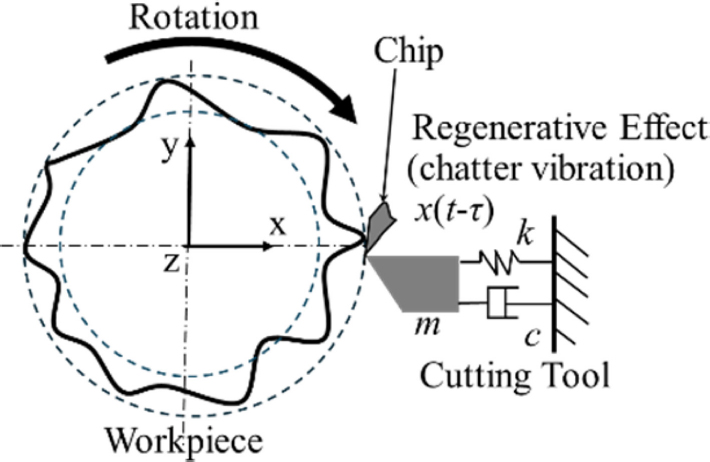
In the present work, a turning operation with a single cutting tool was considered, as shown in Fig. 2. The governing equations of machine chattering can be derived from the general equation of vibration, along with the regenerative chatter equations [17].
In machining stability analysis, chatter is often modeled by a second-order system as Eq. (1):
| (1) |
where y(t) is the displacement, m the effective mass, c the damping, k the stiffness, and F(t) the cutting force [2,4]. Chatter arises from the regenerative effect, where past vibrations influence the current cut [1,2,4]. Therefore, the time-varying chip thickness is in Eq. (2):
| (2) |
involving the nominal chip thickness hₙ and the vibration displacement at a previous revolution x(t-τ), with τ being the rotation time. Assuming a linear cutting force relationship as Eq. (3):
| (3) |
where Kc is the cutting force coefficient, the combined system is described by Eq. (4).
| (4) |
Crucially, x(t-τ) represents the true chatter vibration, delayed by one revolution. To isolate this component, wavelet analysis can be employed to decompose the vibration signal and effectively eliminate the influence of free and forced vibrations, revealing the true chatter vibration x(t-τ) for detailed analysis [2,4,5].
The above mentioned equations are extremely important to comprehend and examine the phenomenon of chatter in machining processes. The equations that allow for the determination of the chip width or depth of cut (bmin) as Eq. (5) in millimeters and spindle speed in revolutions per minute (N) calculate by Eq. (6) in order to construct a SLD [21] are provided as follows:
| (5) |
| (6) |
| (7) |
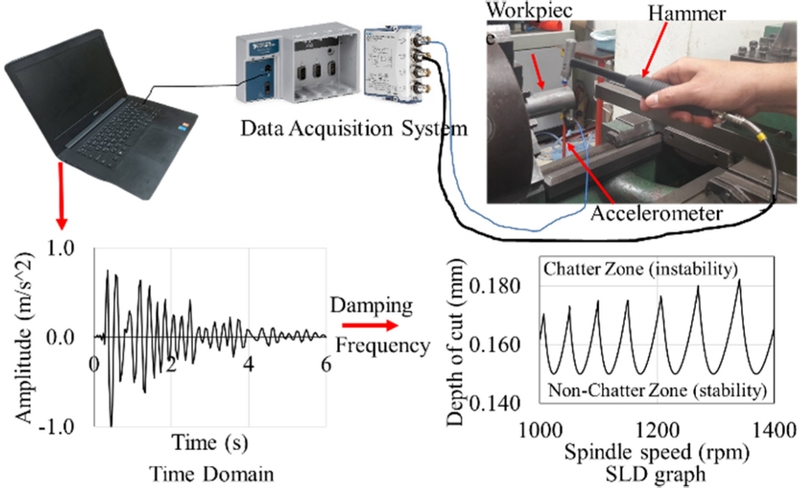
where n is the number of lobes, ζ is the damping ratio Eq. (7), r is the ratio of chatter frequency to the natural frequency (r = f / fn), δ is the logarithmic decrement using ln(x0/x1) for calculation, and x0/x1 are the amplitudes of two successive peaks. This research uses the hammer impact test method with an installed accelerometer LW188088 on the workpiece to sample the vibration signal, as shown in Fig. 3. The detected signal from the hammer test was used to calculate the damping ratio and natural frequency from the time domain of the clamped workpiece on the chuck of the lathe machine [19]. The natural frequency (fn) of the machining system is commonly referred to as the modal frequency. The natural frequency and damping ratio were computed to determine the possible stability boundary in cutting on the stability lobe diagram (SLD) [22]
As shown in Fig. 4, the depth of cut is plotted versus spindle speed in the stability lobe diagram. The vibrations between the tool and the workpiece appear as different lobes (n = 0, 1, 2, ..., last number of lobes) [23].
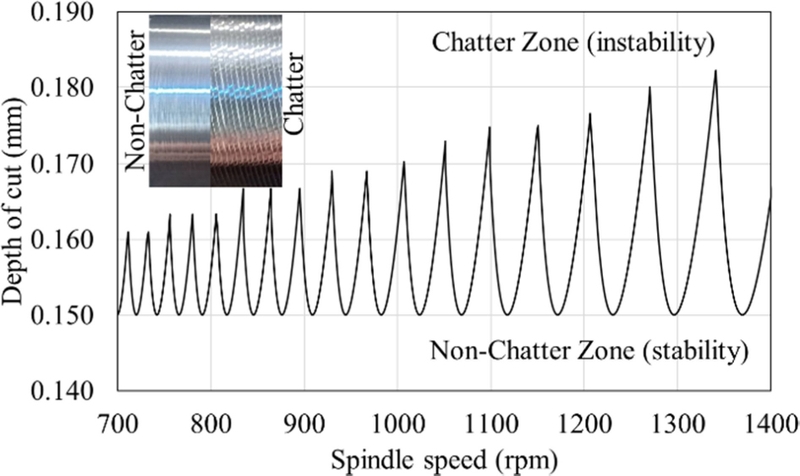
The stability lobe diagram can be derived through modal analysis of the spindle and by considering factors such as the depth of cut and cutting speed [21,24]. The stable region, also known as the stability zone, represents the combination of cutting parameters where chatter vibrations are minimized, resulting in improved tool abrasion, machining surface quality, and productivity. Meanwhile, the unstable region, also known as the instability zone, represents the combination of cutting parameters where chatter vibrations occur, leading to poor machining quality and reduced productivity. The different surfaces of chatter and non-chatter are shown in Fig. 4. The stability lobe diagram is used to determine the optimal cutting parameters that maximize productivity while avoiding chatter vibrations.
2.3 Experiments
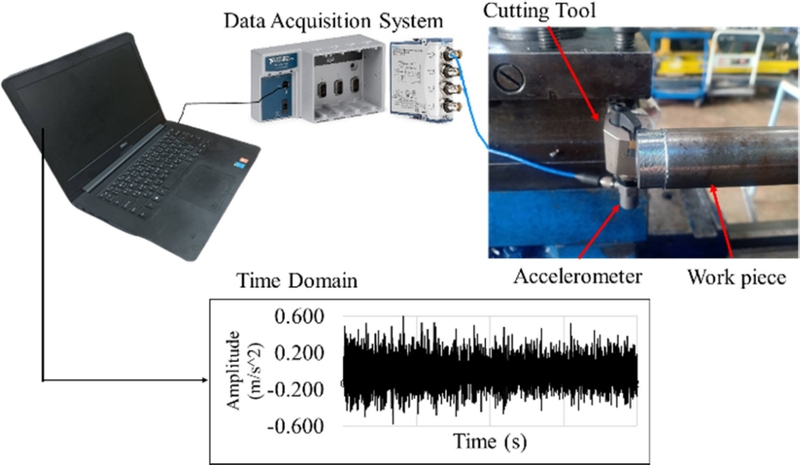
The experiments were performed on a semi-automatic lathe. The cutting tool was equipped with an accelerometer type of vibration sensor to measure the vibration signal and determine the natural frequency of vibrations, as illustrated in Fig. 5. The natural frequency of the cutting tool was examined before being sent to the measuring program to collect vibration signals with a sampling rate of 2,000 Hz and present a real-time graph in the time domain. Experimental cutting operations were conducted using a constant feed rate of 0.8 mm/revolution and two levels of cutting depth: 0.15 and 0.2 mm. The lathe machine gearing system was fixed at spindle speeds of 500, 1,000 and 1,400 rpm that were selected for the experiment. The computed critical depth of cut on each spindle speed is plotted on the SLD graph in Fig. 4.
2.4 Signal Analysis with DWT Denoising Technique
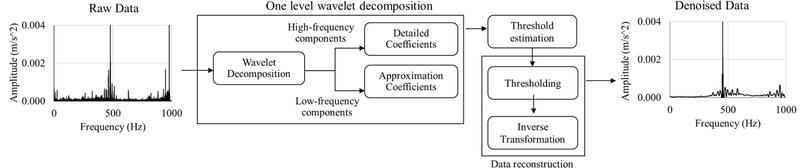
The force and chatter vibration signals in the time domain were converted to the frequency domain [25]. FFT approaches are inefficient for force and chatter signal processing [5] as shown in the example in Fig. 6. Wavelet denoising is a signal processing technique used to reduce noise from signals while preserving important features [26]. Wavelet denoising is particularly effective at removing noise from signals with both low and high-frequency components, making it suitable for a wide range of applications such as vibration and data analysis [12]. The main concept of the denoising technique is shown in Fig. 6. The denoising procedure consists of a sequential process involving three steps.
- 1. Initial Stage: In this stage, the selection of a wavelet and the determination of a level N are undertaken. The signal s is then subjected to wavelet decomposition at level N [27].
- 2. Detail coefficient thresholding: Within each level denoted by integers 1 through N, a distinct threshold value is selected and then applied to the detail coefficients via the use of either soft or hard thresholding methodologies [27].
- 3. Reconstruction: The process of wavelet reconstruction involves the use of the original approximation coefficients at level N and the updated detail coefficients from levels 1 to N [27].
The first stage consists of decomposing the signal contaminated with noise into distinct frequency components using multiple-denoising methods including the Daubechies and Biorthogonal methods in the discrete wavelet transform (DWT) technique [26]. The DWT breaks the signal into a set of wavelet coefficients at different scales and positions. The resulting coefficients represent the signal's frequency content at various resolutions, with the high-frequency coefficients capturing details and noise, while the low-frequency coefficients contain smoother information. The signal passes through a high-pass filter and a low-pass filter. The output of the high-pass filter corresponds to the high-frequency components of the signal, called content components. The output of a low-pass filter matches the lowfrequency components of the signal, called the approximation [28]. After the decomposition, the primary procedure responsible for denoising is the threshold process or wavelet shrinkage, which relies on the selection of a threshold and a thresholding method. In all denoising algorithms, the initial step is to determine the optimal threshold value. The goal of thresholding is to remove or reduce coefficients that represent noise while keeping values that represent important signal features.
Two fundamental types of thresholding functions are hard thresholding and soft thresholding [29]. A hard threshold sets wavelet coefficients with values below a certain threshold to zero. This method effectively removes coefficients that are considered noisy or unimportant, resulting in a sparse representation of the signal. The hard threshold (WH) function is given as:
| (8) |
where W and Tv are the noisy wavelet coefficient and the threshold, respectively. Soft thresholding reduces wavelet coefficients with magnitudes below the threshold towards zero. Unlike hard thresholding, soft thresholding does not remove coefficients completely but rather shrinks their magnitudes.
This method results in smoother denoised signals with reduced noise. The soft thresholding (WS) function is performed with the following conditions [29].
| (9) |
This study used soft thresholding as a signal recovery method because it can mitigate the sudden and dramatic shifts associated with hard thresholding, resulting in a visually more appealing reconstructed signal. The reconstruction process is the final stage. After decomposing the signal into approximation and detail coefficients, the threshold value is determined using a threshold selection rule. Subsequently, the aforementioned value is used to threshold the detailed coefficients. The signal is rebuilt using the original approximation coefficients and the changed detail coefficients after performing thresholding on the detail coefficients [29].
To assess the efficacy of wavelet denoising, the Signal-to-Noise Ratio (SNR) and Mean-Square Error (MSE) were employed as quantitative metrics [30,31]. For a given decomposition level, the SNR, defined as 10 times the logarithm (base 10) of the ratio of signal power to noise power (Eq. (10)), was calculated to evaluate noise reduction [31]. A higher SNR indicates more effective noise suppression. Conversely, the MSE, representing the average squared difference between the original signal and the denoised signal (Eq. (11)), was used to assess signal fidelity preservation [30,31]. A lower MSE indicates better agreement with the original signal. By calculating these metrics for various wavelet bases and decomposition levels, the optimal wavelet parameters for maximizing noise reduction while minimizing signal distortion were determined.
| (10) |
| (11) |
3. Results
3.1 Natural Frequency Investigation
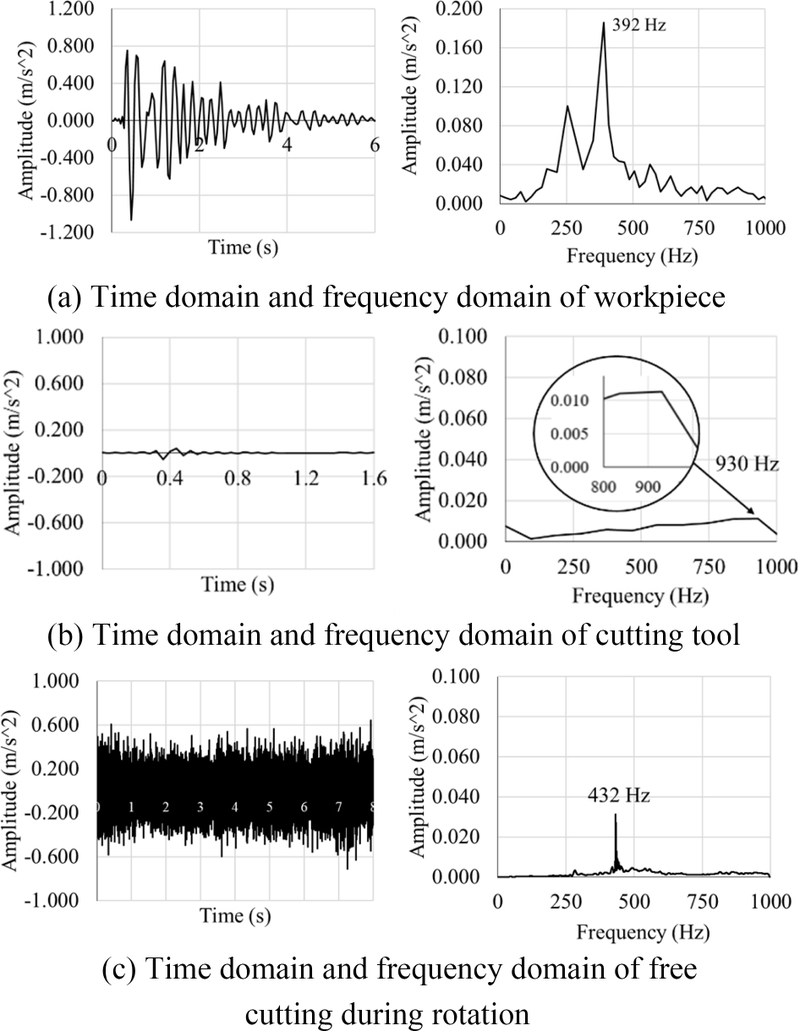
This study analyzes the natural frequency of a self-excited vibrating workpiece and cutting tool by the using a hammer impact test. The detected vibration signal was collected in the time domain pattern and the data was converted to the frequency domain pattern using the FFT technique, as presented in Fig. 7. The time domain characterization of the workpiece signal pattern exhibited a high initial amplitude during the first vibration, followed by a subsequent decrease in oscillation over time. After converting the data into the frequency domain, FFT analysis revealed the presence of two peaks in amplitude. These peaks are seen at frequencies of 280 and 392 Hz, with corresponding amplitudes of 0.1 and 0.16 m/s2, respectively.
The signal pattern of the cutting tool in the time domain exhibited a small range of amplitude and a rapid transition to a stable state. In the FFT analysis, an obvious peak with an amplitude of 0.03 m/s2 could be detected at a frequency of 930 Hz. The time domain analysis for the free cutting of the machine spindle speed reveals a significant range of amplitude and a consistent pattern throughout the period of time. The FFT analysis revealed an obvious peak of significant amplitude at a frequency of 432 Hz, with a maximum amplitude of 0.04 m/s2.
3.2 Stability Lobe Diagram Construction
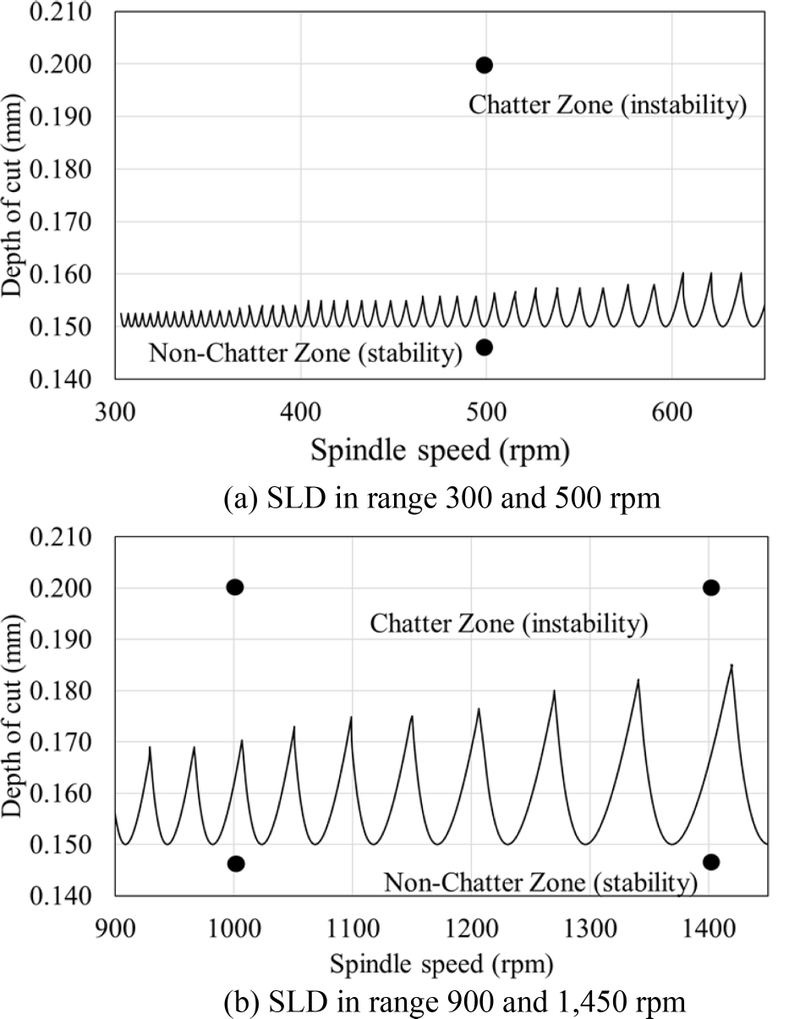
The hammer impact test was used to obtain the vibration characteristic and find the logarithmic decrement, damping ratio, and natural frequency. The results were employed to calculate and plot the SLD graph on each chuck spindle speed of the lathe machine. In Fig. 8(a), the SLD graph was generated to illustrate the regions of instability and stability with respect to the spindle speed, which varied between the values of 0 and 650 rpm. The depth of cut ranged from 0.15 to 0.160 mm. The SLD graph in Fig. 8(b) was constructed to show the spindle speed within the range of 950 and 1,450 rpm. Similarly, the depth of cut spanned from 0.15 to 0.185 mm. In Figs. 8(a) and 8(b), the small circle depicted the chosen cutting depth near the lower curve of the SLD line. The experiments were conducted based on this cutting depth as a cutting parameter.
3.3 Vibration in the Cutting Experiment
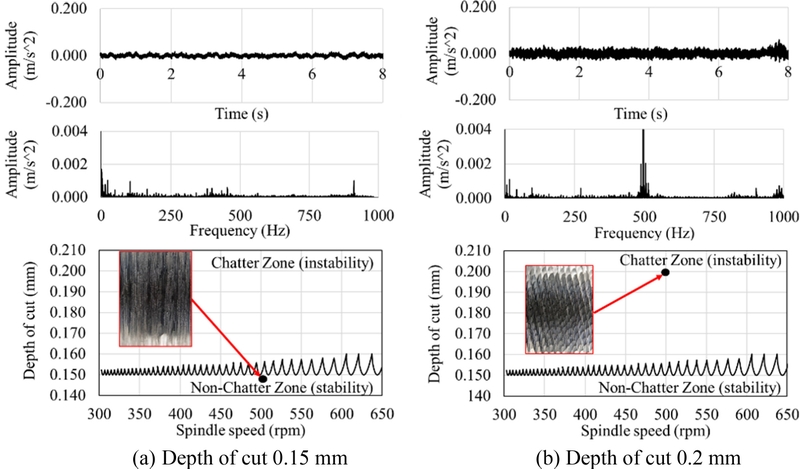
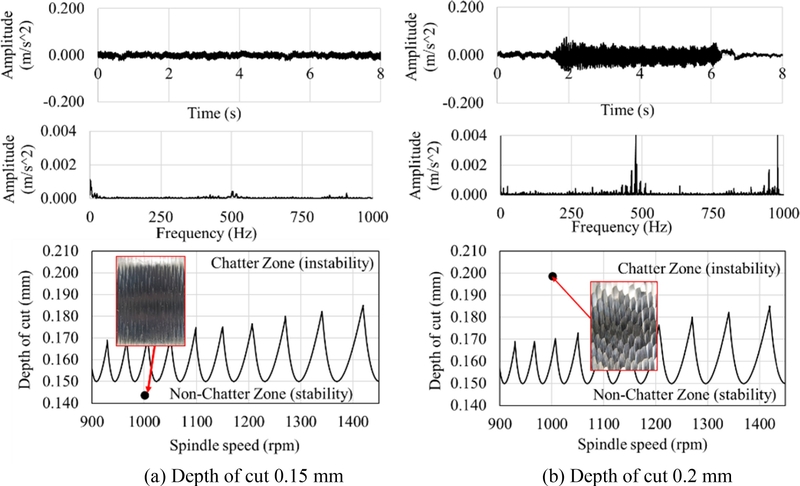
The obtained vibration signal data is presented in Figs. 9, 10 and 11. The experiment demonstrated that increasing the spindle speed of the machine raised the amplitude of the signal in the time domain based on the depth of cut and feed rate constant. The signal with low amplitude resulted in a spindle speed of 500 rpm and a cutting depth of 0.15 mm. The measured signal in the frequency domain presented the small amplitude performed along the frequency axis. The finished cutting surface had a fine roughness, as non-chatter represents the stable state during the cutting, as shown in Fig. 9(a). However, in the frequency domain the minute amplitude was nearly 900 Hz which is the natural frequency of the cutting tool. Fig. 9(b) shows the acquired approximately ± 0.03 m/s2 vibration signal from a cutting depth of 0.2 mm. The results show high amplitude at 500 frequency and small amplitude in the range of 900-1,000 Hz, which is nearly the natural frequency of the cutting tool. The experiment cutting with a spindle speed of 1,000 rpm and 0.2 mm depth of cut obtained intensive vibration signal amplitude approximately ± 0.05 m/s2 in the time domain compared with a depth of cut of 0.15 mm as shown in Fig. 10.
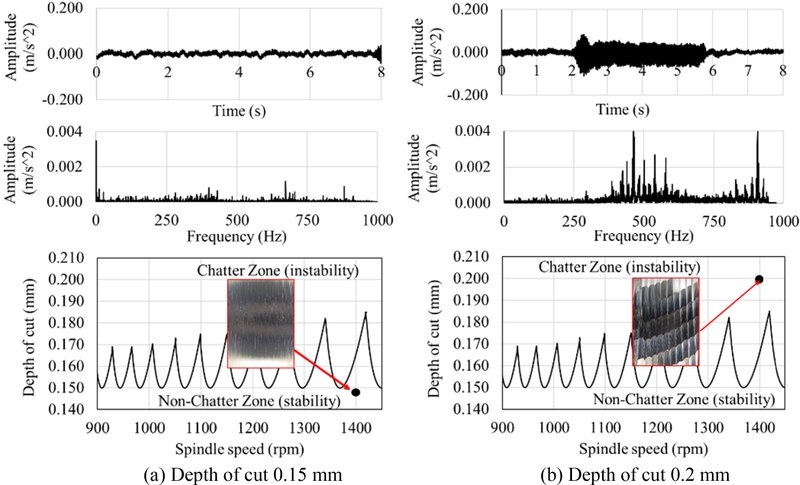
The experiment with a cutting depth of 0.15 mm produced a low amplitude vibration signal along the frequency domain, as illustrated in Fig. 10(a). However, the frequency domain of the experiment with a cutting depth of 0.2 mm exhibited 500 Hz with an elevated amplitude. The raised amplitude was approximately 950 Hz, which aligns with the inherent frequency of the cutting tool, as illustrated in Fig. 10(b). The investigation surface found the fine surface was obtained in the cutting with a depth of cut 0.15 mm and a wavy surface resulted from slight chatter in the depth of cut of 0.2 mm of turning, as shown in Figs. 10(a) and 10(b), respectively. The vibration signal acquired from the spindle speed experiment at 1,400 rpm, employing depths of cut of 0.15 and 0.2 mm, is illustrated in Fig. 10. The experiment with a cutting depth of 0.15 mm produced a low amplitude of vibration along the time in the time domain as clarified in Fig. 11(a). The acquired vibration data exhibited a consistent or uniform frequency domain and the smooth surface was obtained. The experiment conducted with a cutting depth of 0.2 mm yielded an intense amplitude of approximately ± 0.075 m/s2 in the time domain, as illustrated in Fig. 11(b).
The vibration data obtained displayed two distinct peaks in the frequency domain, at 450 and 905 Hz, which are in close proximity to the natural frequency of the cutting tool. The finished surface displayed a wavy texture accompanied by chattering fit to the turning parameters in the instability zone in the SLD graph. Fig. 9 Acquired vibration signal on experiment spindle speed 500 rpm
3.4 Chatter Frequency Analysis by using Propose Method
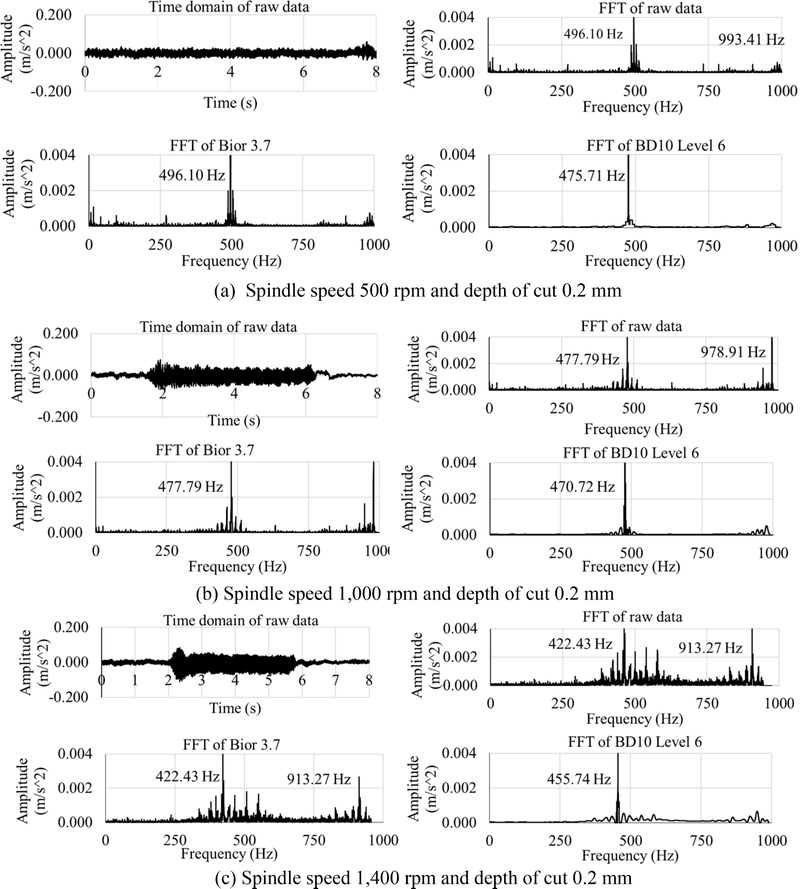
To analyze the chatter frequency, multiple-denoising methods, including Bior 3.7 of biorthogonal and the Daubechies method, were applied to reduce noise in the acquired data. The frequency domain results in Figs. 9(b), 10(b), and 11(b) at a frequency around 900 Hz which is the natural frequency of the cutting tool and mixed with the cutting vibration results. The Bior 3.7 biorthogonal method with 1 level and DB10 in the Daubechies method with six levels as mother wavelet were applied with a thresholding of 50% on each level. After using the Bior 3.7 method to denoise the acquired signal, the raw data in the time domain was filtered to eliminate some noise of the acquired signal. The Bior 3.7 signal feature for each experiment shown in Figs. 12(a)-12(c) decreased the amplitude and lightly intensified of signal. The Bior 3.7 signal feature for the experiment shown in Figs. 12(a)-12(c) decreased the amplitude and lightly intensified in the time domain, but it can efficiently represent signals with non-smooth features [30].
Since biorthogonal wavelets can be useful for applications to maintain certain characteristics during reconstruction, the FFT spectrum was a few signals lower than the raw data in the FFT domain [32]. Therefore, the frequency spectrum around 500 and 900 Hz was substantially reduced. After that, the DB10 in the Fig. 10 Acquired vibration signal on experiment spindle speed 1,000 rpm Fig. 11 Acquired vibration signal on experiment spindle speed 1,400 rpm Daubechies method with six levels was employed to denoise the cutting tool’s natural frequency at 900 Hz.
The proposed multiple-denoising method was able to reduce the amplitude of 900 Hz when the DB10 number of the level was increased. For each experiment in Fig. 12(a)-12(c), the amplitude of 900 Hz nearly reached zero at level six of denoising with the DB10 method. Several noise frequencies around 900 Hz were effectively eliminated. The analyzed results can be compared with high amplitude in the raw data in the FFT spectrum. The spectrum obtained from the denoising process using the DB10 six-level wavelet exhibits a smoother profile compared to the spectrum obtained using the Bior 3.7 wavelet [33].
The higher vanishing moments of DB10 presented in the results make it well-suited for applications [34]. The multiple-denoising method clearly shows chatter frequency in the range of 450-480 Hz for the experiments operated with a depth of cut 0.2 mm at spindle speeds of 500, 1,000, and 1,400 rpm. The frequency exhibits nearuniformity across all signal analyses from each experiment, as generating a chatter frequency at this state. The chatter frequency of this study is equivalent to the findings of Mohsen and Atiyeh [2] where the conversational noise frequency fell within the range of 420-480 Hz.
This study evaluates the performance of different signal filtering methods, including Bior 3.7, DB10 and a multi-denoise approach sequencing Bior 3.7 and DB10, compared to raw data using SNR and MSE. The results were summarized in Table 1.
DB10 generally performed better than Bior 3.7, especially at higher rotational speeds (1,000 and 1,400 rpm). This indicates that DB10 was more suitable for handling signals with higher noise levels. Bior 3.7 showed the weakest performance, particularly at 1,400 rpm, where SNR dropped significantly and MSE increased. The results revealed that Bior 3.7 was not suitable for higher noise Fig. 12 Chatter frequency analysis by using DWT with Bior 3.7 and DB10 levels or faster signal variations.
Multi-denoise was the most robust method, delivering the best performance across all rotational speeds. The proposed method demonstrably enhances signal quality compared to raw data. Consistently achieving the highest SNR and lowest MSE across all conditions tested, the multiple-denoising method outperformed individual wavelet techniques.
4. Conclusion
In this work, the DWT combined with Bior 3.7 and the DB10 method was presented to identify chatter frequency by reducing natural cutting tool noise and noise of free vibration frequency in the turning process. The natural frequency of the cutting tool and workpiece was 930 and 392 Hz when using the hammer impact test. The force vibration frequency from the lathe spindle speed had a small amplitude at 432 Hz. On the SLD graph, critical cutting depths of 0.15 and 0.2 mm were used to examine the turning process on the semi-automatic lathe with spindle speeds of 500, 1,000 and 1,400 rpm. The increased spindle speed activated intense force vibration amplitudes. The increased cutting depth shifted the cutting from the stable zone to the unstable zone, which generated chatter and a wavy surface in the finished turning part.
The multiple-denoising method was applied to analyze the chatter frequency in the acquired data. The Bior 3.7 and DB10 wavelet methods were used with different levels of thresholding to reduce noise and filter the raw data in the time and frequency domains. The Bior 3.7 method decreased the amplitude and intensity of the signal in the time domain, while the DB10 method effectively eliminated noise frequencies around 900 Hz. The denoising process using the DB10 wavelet resulted in a smooth frequency spectrum. The chatter frequency in the range of 450-480 Hz was observed in the experiments. This proposed multiple-denoising method is an effective approach to accurately examine chatter vibrations. These findings provide a strong foundation for further research and development in wavelet-based signal filtering. This research novel can be applied to digital twin technology for real-time online monitoring in machining processes and isolating the chatter vibration signal for predicting machining quality and performance.
REFERENCES
-
Al-Shayea, A., Abdullah, F. M., Noman, M. A., Kaid, H., Abouel Nasr, E., (2020), Studying and optimizing the effect of process parameters on machining vibration in turning process of aisi 1040 steel, Advances in Materials Science and Engineering, 2020(1), 5480614.
[https://doi.org/10.1155/2020/5480614]

-
Emami, M., Karimipour, A., (2021), Theoretical and experimental study of the chatter vibration in wet and mql machining conditions in turning process, Precision Engineering, 72, 41-58.
[https://doi.org/10.1016/j.precisioneng.2021.04.006]

-
Liu, H., He, Y., Mao, X., Li, B., Liu, X., (2017), Effects of cutting conditions on excitation and dynamic stiffness in milling, The International Journal of Advanced Manufacturing Technology, 91, 813-822.
[https://doi.org/10.1007/s00170-016-9809-4]

-
Shrivastava, Y., Singh, B., Sharma, A., (2018), Analysis of tool chatter in terms of chatter index and severity using a new adaptive signal processing technique, Experimental Techniques, 42, 141-153.
[https://doi.org/10.1007/s40799-017-0208-z]

-
Susanto, A., Yamada, K., Tanaka, R., Handoko, Y., Subhan, M. F., (2020), Chatter identification in turning process based on vibration analysis using hilbert-huang transform, Journal of Mechanical Engineering and Sciences, 14(2), 6856-6868.
[https://doi.org/10.15282/jmes.14.2.2020.25.0537]

-
Kounta, C. A. K. A., Arnaud, L., Kamsu-Foguem, B., Tangara, F., (2022), Review of ai-based methods for chatter detection in machining based on bibliometric analysis, The International Journal of Advanced Manufacturing Technology, 122(5), 2161-2186.
[https://doi.org/10.1007/s00170-022-10059-9]

-
Artale, G., Panzavecchia, N., Cosentino, V., Cataliotti, A., Ben- Romdhane, M., Benazza-Ben Yahia, A., Boscaino, V., Ben Othman, N., Ditta, V., Fiorino, M., (2023), Czt-based harmonic analysis in smart grid using low-cost electronic measurement boards, Energies, 16(10), 4063.
[https://doi.org/10.3390/en16104063]

- Shaker, A. N., (2022), Mathematical analysis wavelets characteristics and their applications, International Journal of Nonlinear Analysis and Applications, 13(1), 837-850.
-
Zuo, P., Ma, D., Chen, Y., (2022), Photonics-based short-time fourier transform without high-frequency electronic devices and equipment, IEEE Photonics Technology Letters, 35(2), 109-112.
[https://doi.org/10.1109/LPT.2022.3225547]

-
Yan, Z., Chao, P., Ma, J., Cheng, D., Liu, C., (2021), Discrete convolution wavelet transform of signal and its application on bev accident data analysis, Mechanical Systems and Signal Processing, 159, 107823.
[https://doi.org/10.1016/j.ymssp.2021.107823]

-
Dong, X., Tu, G., Wang, X., Chen, S., (2021), Real-time chatter detection via iterative vold-kalman filter and energy entropy, The International Journal of Advanced Manufacturing Technology, 116, 2003-2019.
[https://doi.org/10.1007/s00170-021-07509-1]

-
Bonda, A. G. Y., Nanda, B. K., Jonnalagadda, S., (2020), Vibration signature based stability studies in internal turning with a wavelet denoising preprocessor, Measurement, 154, 107520.
[https://doi.org/10.1016/j.measurement.2020.107520]

-
Brahimi, M., (2022), Biorthogonal nonstationary and daubechies wavelets: a comparative study, Advances in Mathematics: Scientific Journal, 11(7), 601-612.
[https://doi.org/10.37418/amsj.11.7.4]

-
Shrivastava, Y., Singh, B., (2021), Tool chatter prediction based on empirical mode decomposition and response surface methodology, Measurement, 173, 108585.
[https://doi.org/10.1016/j.measurement.2020.108585]

-
Ahmadi, K., (2017), Analytical investigation of machining chatter by considering the nonlinearity of process damping, Journal of Sound and Vibration, 393, 252-264.
[https://doi.org/10.1016/j.jsv.2017.01.006]

-
Glogowski, P., Rieger, M., Sun, J. B., Kuhlenkötter, B., (2016), Natural frequency analysis in the workspace of a six-axis industrial robot using design of experiments, Advanced Materials Research, 1140, 345-352.
[https://doi.org/10.4028/www.scientific.net/AMR.1140.345]

-
Karimipour, A., Emami, M., (2019), System identification and model predictive control of the chatter phenomenon in turning process, Advances in Science and Technology. Research Journal, 13(3), 217-228.
[https://doi.org/10.12913/22998624/111705]

-
Kosarac, A., Sikuljak, L., Salipurevic, M., Zeljkovic, M., (2020), Comparison of different mathematical models for prediction of self-excited vibrations occurrence in milling process, International Journal of Electrical Engineering and Computing, 3(2), 54-60.
[https://doi.org/10.7251/IJEEC1902054K]

-
Urbikain, G., Olvera, D., López de Lacalle, L. N., Beranoagirre, A., Elías-Zuñiga, A., (2019), Prediction methods and experimental techniques for chatter avoidance in turning systems: A review, Applied Sciences, 9(21), 4718.
[https://doi.org/10.3390/app9214718]

-
Mei, C., Sha, H., (2016), Analytical and experimental study of vibrations in simple spatial structures, Journal of Vibration and Control, 22(17), 3711-3735.
[https://doi.org/10.1177/1077546314565807]

-
Jasiewicz, M., Miądlicki, K., (2019), Implementation of an algorithm to prevent chatter vibration in a cnc system, Materials, 12(19), 3193.
[https://doi.org/10.3390/ma12193193]

-
Ibanez, A. I., Arrazola, P. J., Orskov, K. B., (2020), Workpiece material influence on stability lobe diagram, Procedia Manufacturing, 47, 479-486.
[https://doi.org/10.1016/j.promfg.2020.04.342]

- Kumar, A., Kumar, M., Singh, R., (2018), Chatter stability and tool wear prediction during orthogonal turning by considering sharp tool, International Journal of Applied Engineering Research, 13, 11069-11076.
-
Beri, B., Meszaros, G., Stepan, G., (2021), Machining of slender workpieces subjected to time-periodic axial force: Stability and chatter suppression, Journal of Sound and Vibration, 504, 116114.
[https://doi.org/10.1016/j.jsv.2021.116114]

-
Perrelli, M., Cosco, F., Gagliardi, F., Mundo, D., (2021), Inprocess chatter detection using signal analysis in frequency and time-frequency domain, Machines, 10(1), 24.
[https://doi.org/10.3390/machines10010024]

-
Srivastava, M., Anderson, C. L., Freed, J. H., (2016), A new wavelet denoising method for selecting decomposition levels and noise thresholds, IEEE Access, 4, 3862-3877.
[https://doi.org/10.1109/ACCESS.2016.2587581]

-
Chen, S.-W., Chen, Y.-H., (2015), Hardware design and implementation of a wavelet de-noising procedure for medical signal preprocessing, Sensors, 15(10), 26396-26414.
[https://doi.org/10.3390/s151026396]

-
Rahim, A. A. A., Abdullah, S., Singh, S. S. K., Nuawi, M. Z., (2020), Selection of the optimum decomposition level using the discrete wavelet transform for automobile suspension system, Journal of Mechanical Science and Technology, 34, 137-142.
[https://doi.org/10.1007/s12206-019-1213-1]

-
Kumar, S., Singh, B., (2019), Chatter prediction using merged wavelet denoising and anfis, Soft Computing, 23, 4439-4458.
[https://doi.org/10.1007/s00500-018-3099-8]

-
Ouyang, C., Cai, L., Liu, B., Zhang, T., (2023), An improved wavelet threshold denoising approach for surface electromyography signal, EURASIP Journal on Advances in Signal Processing, 2023(1), 108.
[https://doi.org/10.1186/s13634-023-01066-3]

-
Liu, Z., Feng, X., Dong, C., Jiao, M., (2023), Study on denoising method of photoionization detector based on wavelet packet transform, Chemosensors, 11(2), 146.
[https://doi.org/10.3390/chemosensors11020146]

-
Tiwari, R., Rekapalli, R., Tiwari, R., Rekapalli, R., (2020), Singular spectrum vs. Wavelet based denoising schemes in generalized inversion based seismic wavelet estimation, Modern Singular Spectral-Based Denoising and Filtering Techniques for 2D and 3D Reflection Seismic Data, 103-108.
[https://doi.org/10.1007/978-3-030-19304-1_9]

-
Abhishek, S., Veni, S., Narayanankutty, K., (2019), Biorthogonal wavelet filters for compressed sensing ecg reconstruction, Biomedical Signal Processing and Control, 47, 183-195.
[https://doi.org/10.1016/j.bspc.2018.08.011]

-
Li, Y., Lu, J., Wang, L., Yahagi, T., (2006), Removal of gaussian noise from degraded images in wavelet domain, IEEJ Transactions on Electronics, Information and Systems, 126(11), 1351-1358.
[https://doi.org/10.1541/ieejeiss.126.1351]


Doctoral Student in Graduate School, King Mongkut’s University of Technology North Bangkok, Bangkok. Her research interest is Mechanical Engineering Education.
E-mail: s6102017910081@email.kmutnb.ac.th

Associate Professor at Department of Teacher Training in Mechanical Engineering, Faculty of Technical Education, King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand. His research interest is Mechanical and Manufacturing Design, Machine Tool and Applied AI for Engineering.
E-mail: bandit.s@fte.kmutnb.ac.th