PET 필름의 로터리 다이 커팅에서 칼날 동작에 따른 응력-변형 및 커팅 힘의 유한요소해석 연구

1. 서론

자동차의 자율주행 및 친환경 전동화에 따라 주행정보, 차량 상태 및 엔터테인먼트 컨텐츠 등을 제공하는 클러스터(Cluster), CID (Center Information Display), 디지털 사이드 미러 등과 같은 디지털 자동차 디스플레이(Automotive Display)의 수요가 증가하고 있다[1]. 자동차 디스플레이 모듈 의 광학 부품으로서 백플레이트(Backplate), OCA (Optical Clear Adhesive) 필름, 광 확산필름 등 다양한 광기능성 필름이 사용되는데, 이들 폴리머 필름의 고정밀, 고속 절단 가공기술은 디스플레이 모듈의 생산성과 품질수준에 큰 비중을 차지한다[2-4].

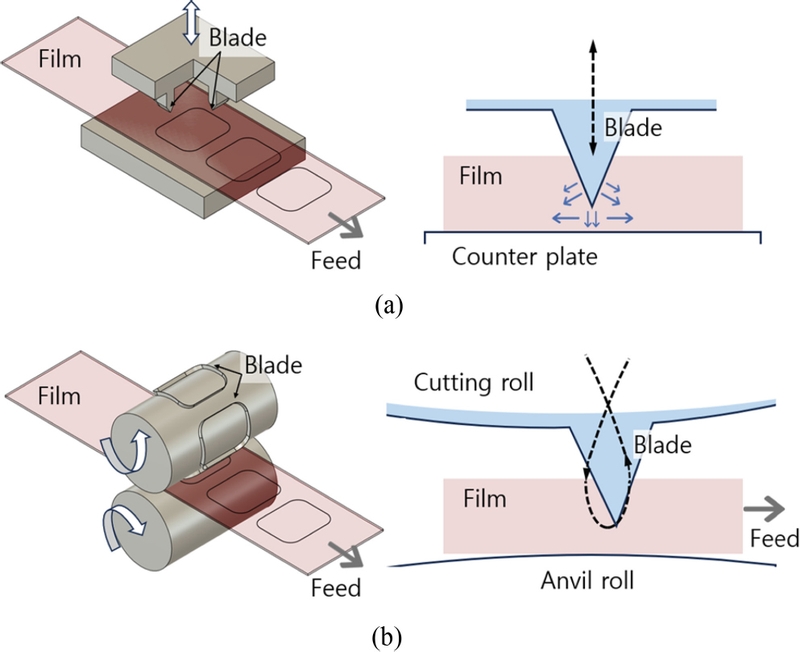
필름 재료를 임의의 형상으로 도려내는 가공기술로서 Fig. 1(a)에 나타낸 방법과 같이 쐐기(Wedge) 형상의 칼날(Blade)을 재료에 압입하는 다이 커팅(Die-cutting) 기술이 있다. 다이 커팅은 종래부터 각종 인쇄물의 절단공정에 사용되었는데, 최근 칼날의 고정밀 가공기술로 칼끝 폭이 수 μm 수준으로 예리(Sharp)해지고 칼날 표면에 기능성 코팅기술이 구현되어 디스플레이, 전자, 의료 부품용 난가공성 필름들의 정밀가공에도 적용되고 있다[5,6]. 특히, 생산성 증대의 요구에 따라, 전통적인 수직 타발 방식의 속도한계를 극복하기 위해 Fig. 1(b)와 같은 롤투롤(Roll-to-roll) 방식의 로터리 다이 커팅(Rotary Die-cutting)이 활용되고 있다 [7-9]. 로터리 커팅은 회전 다이에 의해 연속 가공되므로 고속· 대량생산에 적합하고, 커팅 롤러과 서포트(Support) 롤러 혹은 앤빌(Anvil) 사이의 간격을 정밀하게 조정하여 칼날의 압입 깊이를 조절할 수 있어 다층 복합 필름 가공에 더욱 적합하다[10-12].

Fig. 1

Schematic and blade trajectory of vertical (a) and rotary diecutting (b)

수직 다이 커팅은 칼날의 피가공재료로의 압입-개구(Opening)에 의한 모드 I 파단이다[13,14]. Fig. 1(a)의 우측 그림과 같이 칼날 선단 앞의 세로방향 압축과 가로방향 인장 변형이 파단 (Fracture)을 일으킨다. 수직 커팅은 페이퍼보드, 폴리카보네이트 (Polycarbonate), 감압 점착(Pressure Sensitive Adhesive) 필름에 대해 커팅 힘 및 응력-변형 특성과 연구되었고[15-17], 칼날의 예리함에 관련된 형상 변수(중심각도 및 선단 폭)가 최대응력과 크랙생성의 주요 영향 인자로 분석되었다[15,18,19].

로터리 다이 커팅은 필름의 진행방향에 대한 칼날의 방향에 따라 특성이 달라진다. 슬릿팅(Slitting)은 필름 웹(Web)의 폭을 줄이는 공정으로서, 칼날이 필름 진행방향과 항상 나란하므로 커팅 힘의 변화가 완만하고 가공힘도 수직 커팅에 비해 작다 [14,20-22]. 그러나 로터리 다이 커팅은 칼날 방향이 임의적이다. Fig. 1(b)의 우측 그림처럼 필름 진행방향에 대해 직교하는 칼날은 압입-퇴거가 수직 커팅처럼 단속적이며, 칼날 궤적은 필름에 대해 사이클로이드(Cycloid) 곡선으로 상대 운동한다. 로터리 다이 커팅에서 칼날-피가공 재료간 작용 메커니즘 이해는 필름 부재의 생산기술로서 매우 중요하다. 로터리 커팅은 롤투롤 방식의 복합적 시스템에 기반하므로 품질과 생산성을 유지하기 위해서 공정 중의 주요 인자의 영향을 파악할 필요가 있다. 특히 수직 커팅과 달리 필름의 공급 방향으로 커팅 힘이 발생하고 이로 인해 필름의 변형과 응력에 변화가 유발되기 쉽다. 그러나 칼날의 궤적을 고려한 로터리 다이 커팅의 역학적 거동에 관한 연구 보고는 현재까지 찾아보기 어렵다. 다양한 사례와 메커니즘 분석 연구가 행해진 수직 다이 커팅과 달리, 로터리 커팅의 경우 롤투롤 시스템 등 복잡한 장비가 필요함에도 불구하고 상세한 메커니즘 연구가 없어 개발현장에서는 각종 변수를 경험적 방법에 의존하는 문제가 있다.

본 연구에서는 로터리 다이 커팅 공정의 기본적 역학 거동을 파악하기 위하여, 칼날과 단층 필름의 2차원 해석모델에 기반한 유한요소해석을 수행하였다. 먼저 광학필름으로 매우 빈번히 사용되는 Polyethylene Terephthalate (PET) 필름의 인장시험을 통해 응력-변형율 특성을 측정하였다. 해석모델의 적정성 검증을 위해, 수직 다이 커팅시의 변위-힘을 측정하고 이를 모델링에 의한 수치해석 결과와 비교하였다. 로터리 커팅 과정의 응력과 힘 특성의 해석결과를 분석하고 칼날 선단 각도, 필름 장력, 필름 이송속도의 영향을 파악하고자 하였다.

2. 실험 및 유한요소해석 방법

2.1 재료와 실험 방법

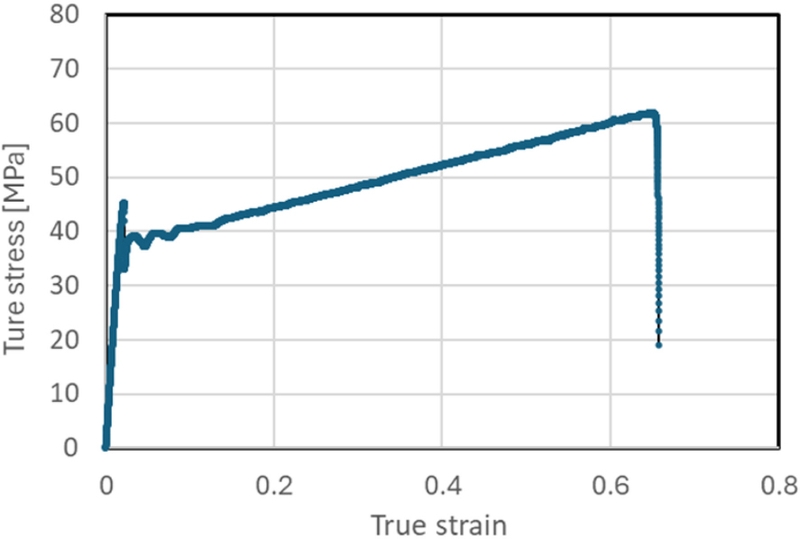
실험 및 해석의 대상 재료는 비결정성(Amorphous) PET 단층 필름(ρ = 1.38 g/cm³)이다. 만능재료시험기(Instron 3345)를 이용한 인장시험을 실시하여 해석에 적용할 기계적 물성치를 확보하였다(ASTM D882). 시편의 크기는 150 × 10 × 0.3 mm³이며 변형속도는 10 mm/min으로 하였고, 클립온(Clip-on) 신율계 (Instron 2630)을 이용하였다. 샘플은 5회 반복 측정하여 평균에 가까운 응력 선도를 채택하였고 그 결과를 Fig. 2에 나타내었다. 측정데이터로부터 탄성계수는 변형율 0-1% 구간에 대해 Secant 법에 의해 평가하였고, 항복강도는 0.2% 옵셋 기준을 적용하였으며 Poisson비는 참고문헌의 값을 이용하였다[17]. Table 1에 측정결과를 요약하였다.

Fig. 2

True stress-true strain curve of PET film

Table 1

Mechanical properties of PET

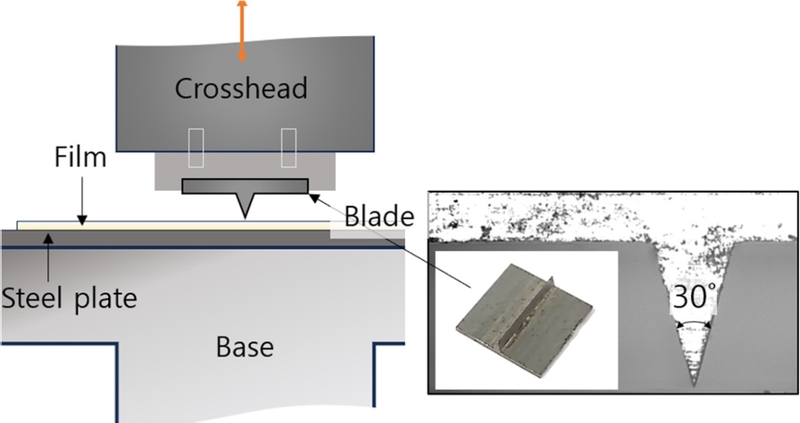
Fig. 3에 수직 다이 방식 실험장치의 개요를 나타내었다. 수직 다이 커팅 실험으로 인장시험 재료와 동일한 PET 필름의 커팅 힘-변위를 파악하여 해석모델을 검증하는데 활용하였다. 만능재료시험기(Instron 3345, USA) 크로스헤드에 칼날 다이를 장착하였고, PET 필름은 하측 베이스 상의 SCM440 플레이트에 두었다. 커팅용 다이는 SK5 재료로서 20 × 20 mm² 블록을 마이크로밀링 가공하여 1.4 mm 높이와 30^o의 선단각을 갖는 칼날을 제작하였다. 필름 상면에서 깊이 0.25 mm까지 칼날을 하강하는 동안 힘을 측정하였다.

Fig. 3

Experimental setup of vertical die cutting

2.2 유한요소해석 방법

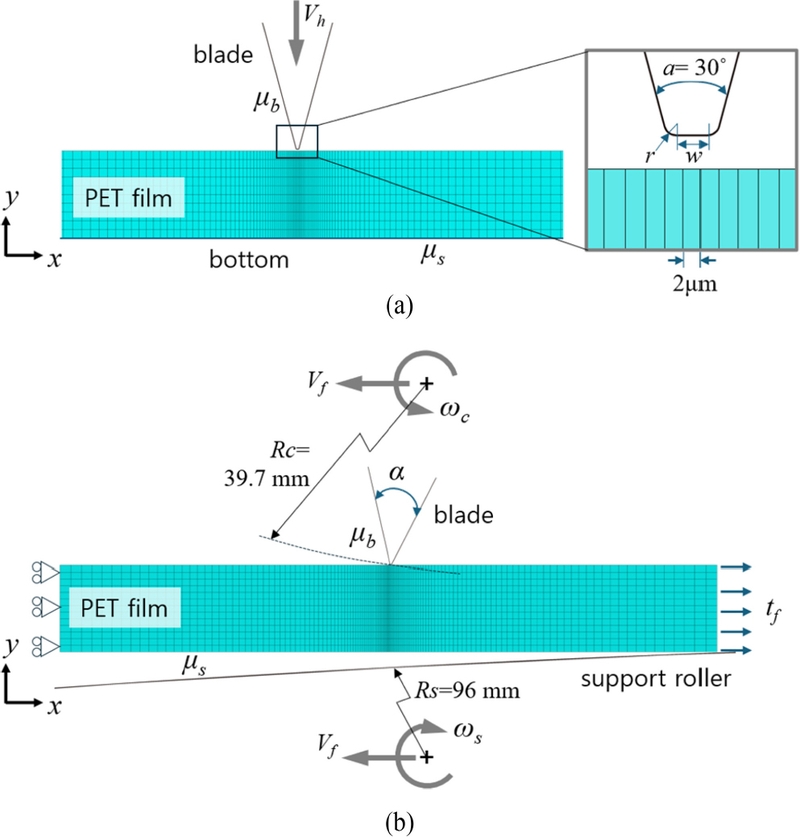
필름의 커팅 해석을 위해 Abaqus/Explicit를 이용하였고, 평 면응력을 가정하여 2차원 해석을 수행하였다. Fig. 4(a)에 수직 커팅 모델을 제시하였다. PET 필름은 Fig. 2의 실험 데이터를 바탕으로 탄소성 재료로 모델링하였고, 나머지는 모두 강체로 간주하였다. PET 필름은 길이 3 mm, 두께 0.3 mm로 설정하고, 2차원 평면응력을 위한 4절점 요소(Mesh)를 적용하였다. 필름은 중앙과 양단의 세 구간(Section)으로 나누어 해석하였으며, 계산의 효율성을 고려하여 필름 중앙부에서 요소의 가로길이를 2에서 20 μm까지 점진적으로 증가시켰다. 모든 요소의 세로길 이는 30 μm로 일정하게 설정하였다. 칼날에 인접한 요소에서 변형이 크게 발생하기 때문에 해석과정에서 요소 오류를 최소화하기 위해 중앙부 요소에는 적응형 메시(ALE Adaptive Mesh)를 적용하였다.

Fig. 4

Schematical representation of the FEA model for vertical die cutting (a) and rotary die cutting (b)

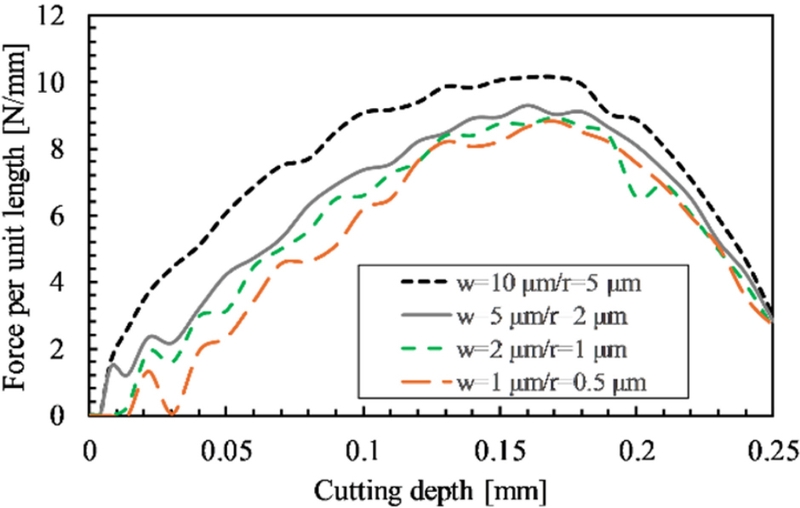
칼날 선단부는 그림과 같이 폭(w)과 모서리 반경(r)으로 모델링하였다. 선단부 치수는 실제를 정확히 반영해야하지만, 해석의 안정성과 계산 효율성에 크게 영향을 미치므로, 필름의 요소 분할 크기와 함께 신중히 고려해야 한다. 본 연구에서는 칼날의 폭/반경은 1/0.5, 2/1, 5/2, 10/5 μm으로 설정하여 계산결과를 먼저 비교한 후, 최적값을 선택하고자 하였다. 선단각(α)은 수직 커팅에서 실험에 사용한 실제 칼날의 각도와 동일하게 30^o로 고정하였다. 또한 칼날-필름, 필름-서포터 롤러 표면 사이에 쿨롱 (Coulmob) 마찰계수(μ_b, μ_s)는 0.1-0.5 범위에서 설정하고 실험 결과에 근접한 값을 선택하였다.

Fig. 4(b)에 로터리 커팅 모델을 나타내었다. 커팅 롤러와 서포트 롤러 각각 각속도 ω_c, ω_s와 수평이동속도 V_f = 100 mm/s를 부여하였으며, 필름에는 이송 장력(t_f)을 적용하였다. 칼날의 압입 과정에서 운동에너지가 충분히 낮아, 해석은 준정적(Quasi-static) 방식으로 수행되었으며 필름의 균열과 파단은 정의하지 않았다.

수직 커팅 과정에 대한 평면해석 계산 결과로서 칼날의 변위에 따른 작용력(=단위 길이당 커팅 힘) 그래프를 Fig. 5에 나타 내었다. 칼날이 필름을 압입시 응력과 접촉면적 증가와 함께 작용력이 증가하다가 연신한도 이후에 다시 감소하는 실제의 경향을 잘 나타내었다. 여기서 칼날의 폭과 반경이 작을수록 힘이 줄어들고, 동시에 접촉해석의 불안정성에 따른 떨림이 증가함을 알 수 있다. 커팅 힘 최대값 기준으로 칼날폭 1, 2, 5 μm에서의 결과가 유사하다고 보고 계산효율성을 위해 칼날의 폭 5 μm, 모서리 반경 2 μm으로 결정하였다.

Fig. 5

Calculation results for four blades with different widths and edge radii: cutting-force relationship in vertical cutting

3. 결과

3.1 수직 커팅

3.1.1 필름의 변형 및 응력 해석결과

Fig. 6은 수직 커팅시 칼날 깊이가 0.12와 0.24 mm일 때 필름의 최대 주변형율(Maximum Principal Strain) 벡터와 von-Mises 응력 분포를 나타낸다. Fig. 6(a)에서 칼날 바로 아래는 인장변형이, 칼날 좌우 측면과 주변부에서는 압축변형이 발생하며, 커팅 깊이 증가에 따라 칼날 아래 인장 변형이 더욱 증가함을 확인할 수 있다. 이러한 변형거동에 따라 Fig. 6(b)의 응력 분포에서는 칼날 아래 필름의 넥킹(Necking) 현상이 나타나며 이 부위에서 응력이 최대화되었다. 또한 변형 거동으로 인해 칼날 측면과 필름 사이에는 비접촉 틈새가 형성되며, 칼날의 측면 전단에 의해 필름 상면의 눌림(Rollover) 현상이 발생하는 것도 확인할 수 있었다.

Fig. 6

FEA results for vercal die Cutting (cutting depth: 0.12 mm on the left, 0.24 mm on the right)

3.1.2 커팅 힘-변위 관계 분석

Fig. 7에 만능재료시험기를 이용한 수직 커팅 실험에서 얻은 힘-변위 데이터와 해석결과로 얻은 힘-변위 데이터를 함께 도시 하였다. 여기서 힘은 평면 해석에 따른 단위 길이당 힘(Cutting Line Force)으로 표현되었다. 해석 결과는 마찰계수에 따른 차 이를 비교하여 분석하였다. Fig. 7(a)는 필름 바닥의 마찰계수를 고정(μ_s = 0.3)하고, 칼날의 마찰계수(μ_b)가 0.1-0.4일 때의 결과이다. 해석결과에서는 마찰계수가 증가함에 따라 기울기(힘/변위)가 커지고 최대 힘도 증가하는 경향이 뚜렷하게 관찰되었다.

Fig. 7

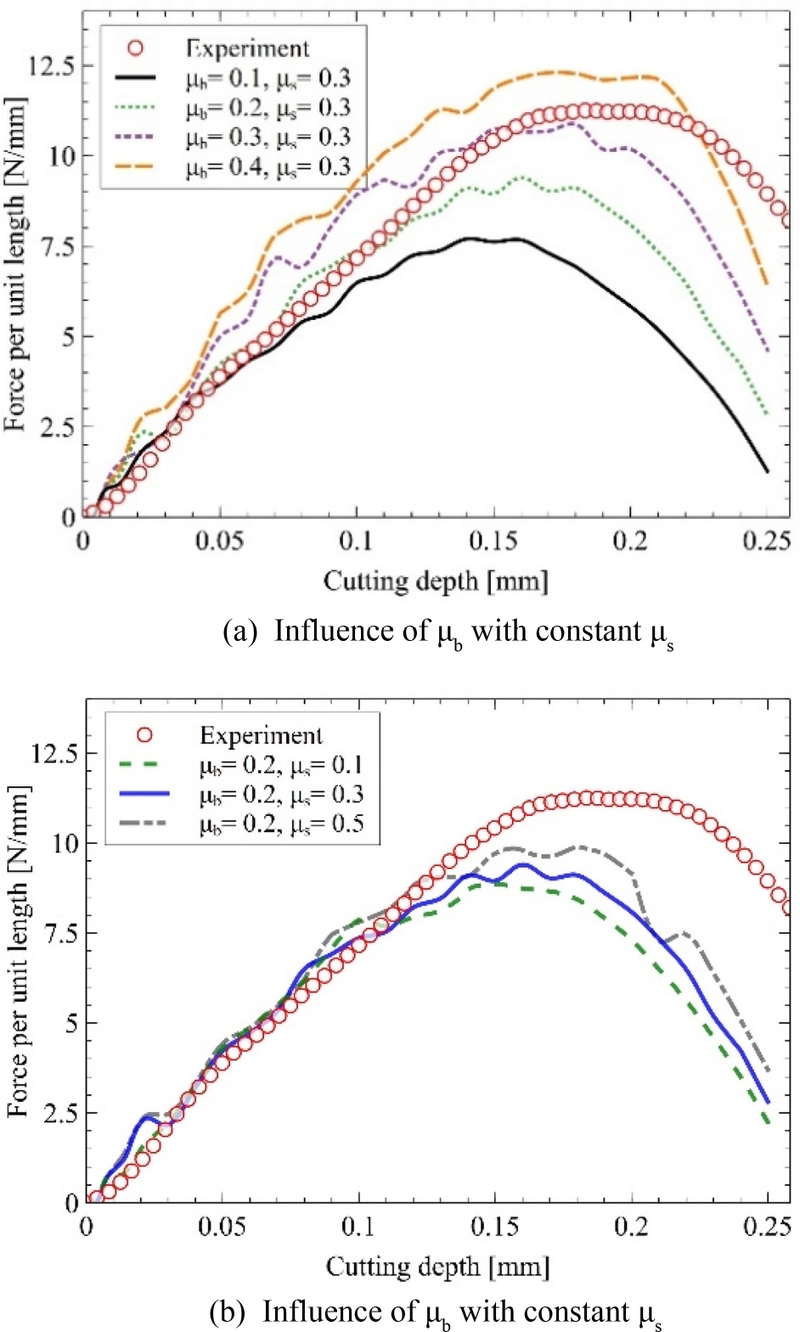
Comparison of experimental result of cutting line force with cutting depth and simulation results considering the effect of friction coefficient

실험에서는 해석결과에 비해 커팅 힘의 변곡이 지연되어 나타났다. 커팅 깊이 0.15 mm 미만에서 기울기를 기준으로 판단할 때, μ_b = 0.2가 실험 결과와 가장 유사한 값을 보였다.

Fig. 7(b)에서는 μ_s를 0.1, 0.3, 0.5로 했을 때의 결과를 도시하였으며, 바닥면의 마찰계수는 커팅 힘에 미치는 영향이 미미함을 알 수 있었다. 비록 실험 결과와 다소 오차가 존재하지만, 본 해석 모델은 실제 커팅 과정을 충분히 설명할 수 있는 수준으로 판단된다. 따라서 로터리 커팅 해석에서는 마찰계수를 μ_b = 0.2, μ_s = 0.3으로 설정하여 진행하였다.

3.2 로터리 커팅 해석

3.2.1 필름의 변형 및 응력해석 결과

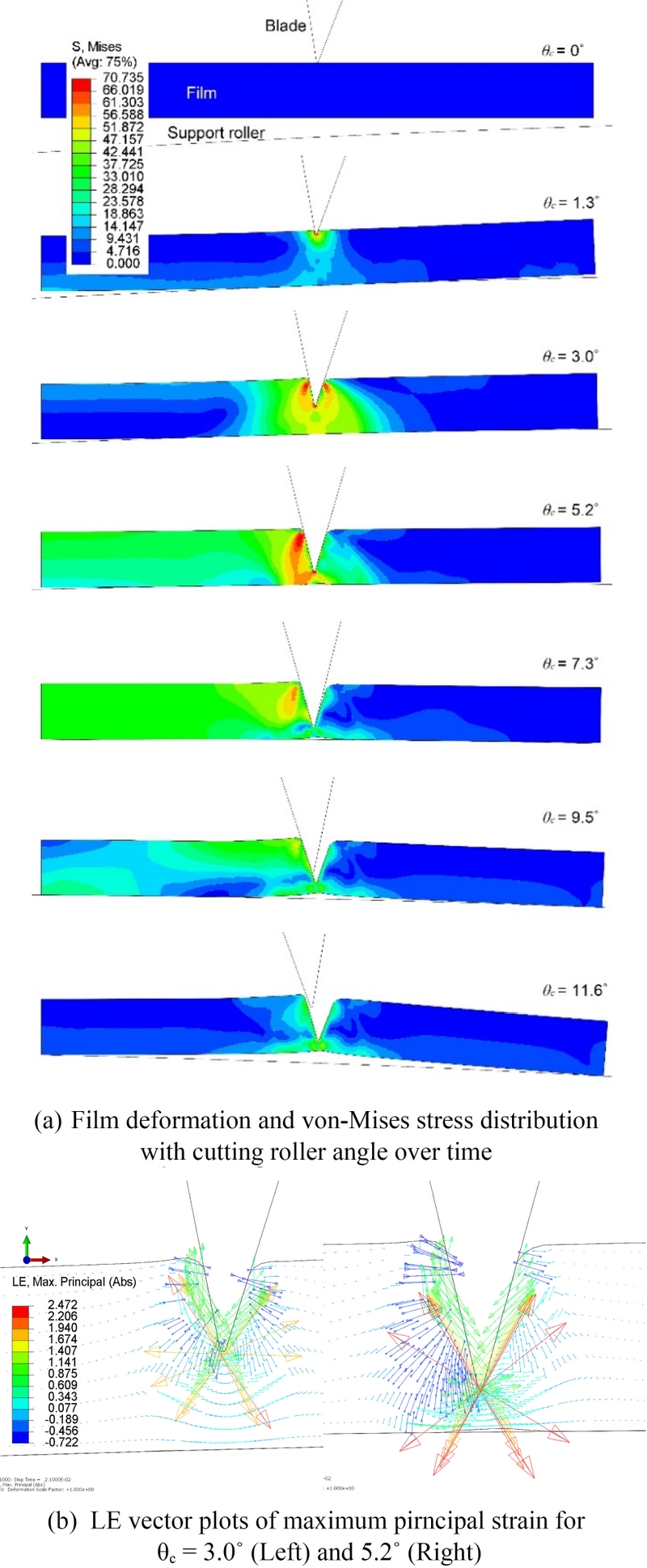
Fig. 8은 로터리 커팅시 선단각 30^o를 갖는 칼날의 회전각(θ_c)에 따른 von-Mises 응력 분포와 2개 회전각에서 주 변형율 분포를 나타낸 것이다. 필름의 장력(t_f)은 2 N/mm으로 설정하였다. θ_c = 1.3^o에서 필름은 서포트 롤러에 밀착되고 칼날이 필름을 파고들기 시작한다. 칼날 아래에서는 강한 인장응력이 발생하며, 이는 수직 커팅에서와 유사한 결과를 보인다. 그러나 θ_c = 5.2^o에서는 칼날 좌우에서 비대칭성이 두드러지는데, 오른쪽으로 진행하는 필름에 대해 칼날은 왼쪽 아래로 압입되면서 왼쪽에서 압축응력이 발달한다. 칼날은 반시계방향으로 자세를 바꾸고 (θ_c= 7.3^o), 오른쪽 위로 칼날이 퇴거하는 움직임이 관찰된다 (θ_c = 9.5^o, 11.6^o). 가공과정에서 필름의 장력이 모멘트를 유발하여 가공 홈이 가공홈이 더 벌어지며, 로터리 커팅의 특성을 나타낸다. 최대응력과 변형률 값은 수직 커팅과 큰 차이가 없으나, 필름 진행방향(X 방향)으로 발생하는 커팅 힘이 공정 품질에 중요한 영향을 미칠 수 있다. 이를 고려하여 주요한 영향 요인을 살펴보았다.

Fig. 8

FEA results for rotary die cutting (Tip angle 30o)

3.2.2 칼날 선단각도의 영향

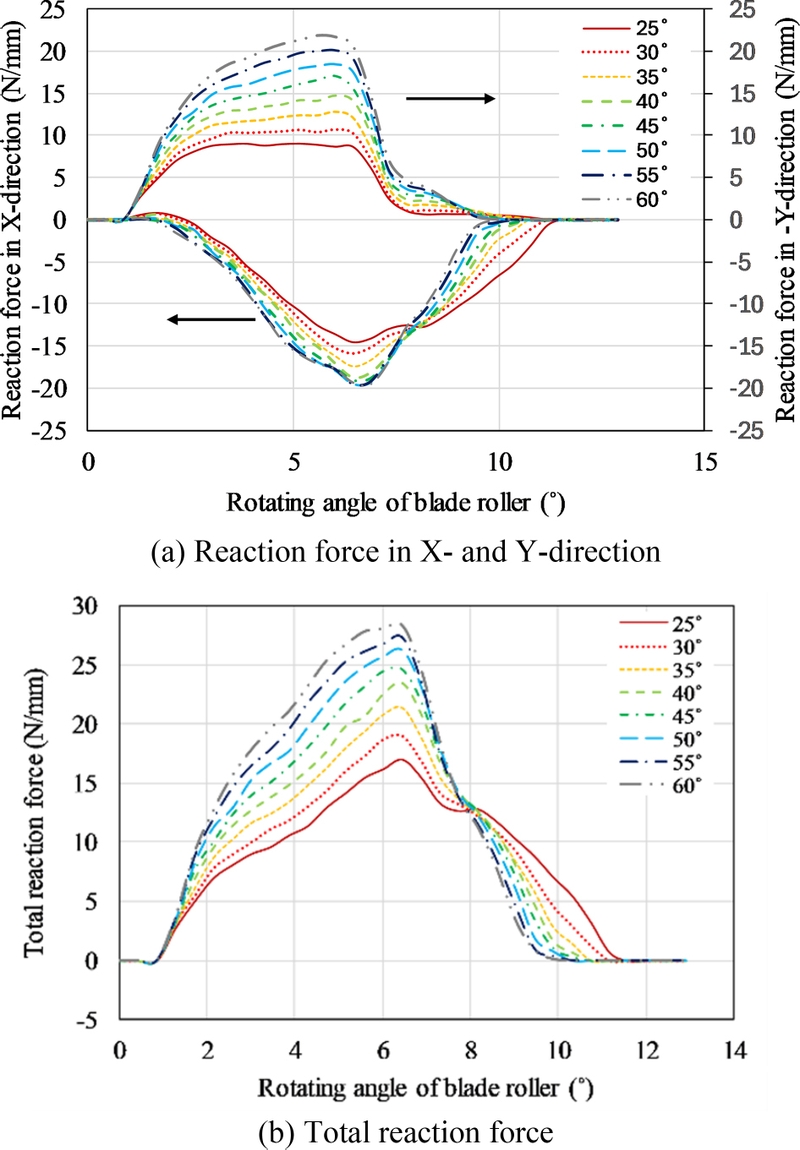
로터리 칼날의 선단각이 25^o에서 60^o까지 변화할 때, 커팅 롤러의 회전각도에 따른 X, Y 방향의 작용력(Reaction Force)을 계산하여 Fig. 9에 나타내었다. 여기서 작용력은 롤러의 중심의 반작용력으로서 커팅 힘으로 간주할 수 있다.

Fig. 9

Variation of reaction force with rotating angle of cutting roller at different blade tip angles

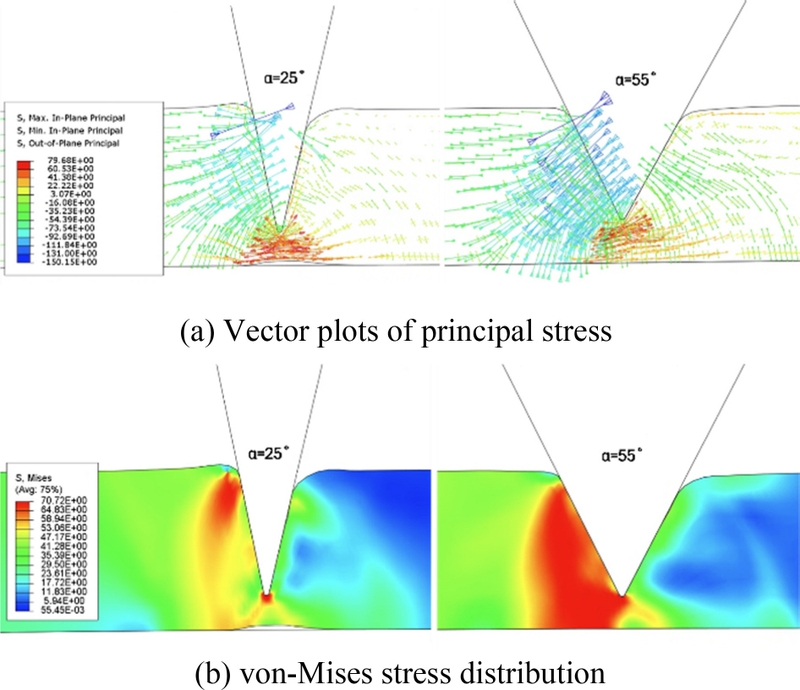
칼날의 압입이 시작되면 Y 방향 힘이 X 방향보다 먼저 증가한다. 선단각이 클수록 변형 저항이 커지므로, 25^o에서 9 N/mm에서 시작된 Y 방향 작용력 절대값이 60^o에서는 22 N/mm까지 증가하였다. X 방향 힘은 Y 방향보다 느리게 발달하며, 선단각이 작을수록 작용력이 감소하지만 작용 각도구간은 넓어지는 특징을 보인다. Fig. 9(b)에 나타난 총 작용력에서도 확인할 수 있듯, 선단각이 클수록 커팅 힘은 증가하지만 필름과의 접촉시간은 짧아진다. 선단각이 각각 25^o, 55^o인 칼날에 의한 필름의 주응력(Principal Stress) 벡터 플롯을 Figs. 10(a)에, von-Mises 응력분포를 10(b)에 나타내었다. 회전각은 5.6^o일 때로서 칼날이 최대깊이에 이를 때이다. 선단각이 작은 25^o에서 선단 하부의 인장 주응력이 더 크고 넥킹이 뚜렷히 발생하였다. 또한 칼날 측면의 압축응력은 좌측 필름 표면근처에 집중되고 필름의 소성흐름에 의한 표면융기가 관측되었다. 반면 선단각 55^o 경우에는 칼날 경사면의 압입에 의한 압축 주응력(최소 주응력)이 강하고 넓게 분포하며, 선단 하부의 인장 주응력은 25^o 선단각에 비해 작아 넥킹이 거의 일어나지 않았다.

Fig. 10

FEA results for rotary die cutting (Blade tip angle: 25o on the left, 55o on the right)

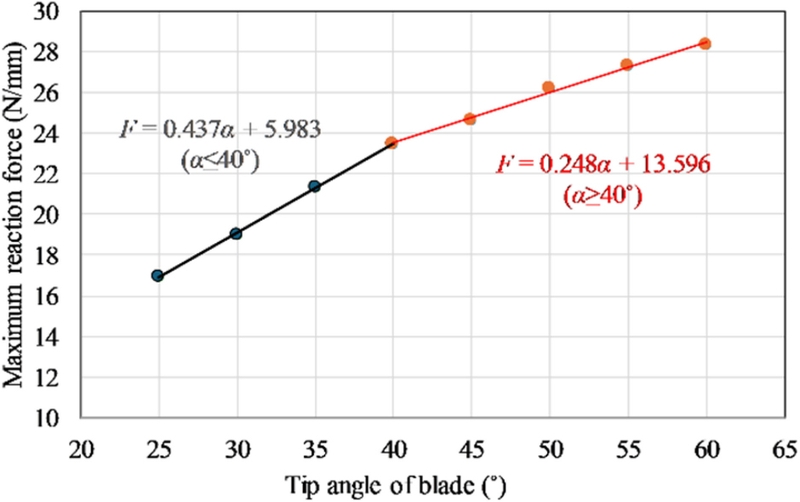
Figs. 11에 선단각에 따른 최대 커팅 힘(Maximum Reaction Force)을 9의 결과를 이용하여 나타내었다. 최대 힘은 선단각과 선형 비례관계에 있으나 선단각 약 40^o 부근에서 기울기의 변화를 확인할 수 있는데 이는 다음의 1차식으로 피팅할 수 있다.

Fig. 11

Variation of maximum reaction force as a function of tip angles of blade

$\[ F=0.437\alpha +5.983\left(\alpha \le {40}^{\circ }\right) \]$

(1)

$\[ F=0.248\alpha +13.60\left(\alpha \ge {40}^{\circ }\right) \]$

(2)

Fig. 10에 나타낸 것처럼, 선단각 증가에 따라 경사면 부근의 압축응력이 확대되고 접촉면이 증가하는데 40^o 부근부터 선단각의 민감도가 변화하는 것으로 판단된다.

선단각은 롤 시스템 설계에서 중요 인자이며 가공성과 수명 등을 추가로 고려할 필요가 있다. 이후 로터리 커팅 해석에서는 선단각을 40^o로 고정하였다.

3.2.3 로터리 커팅 공정인자의 영향

3.2.3.1 필름장력 변동

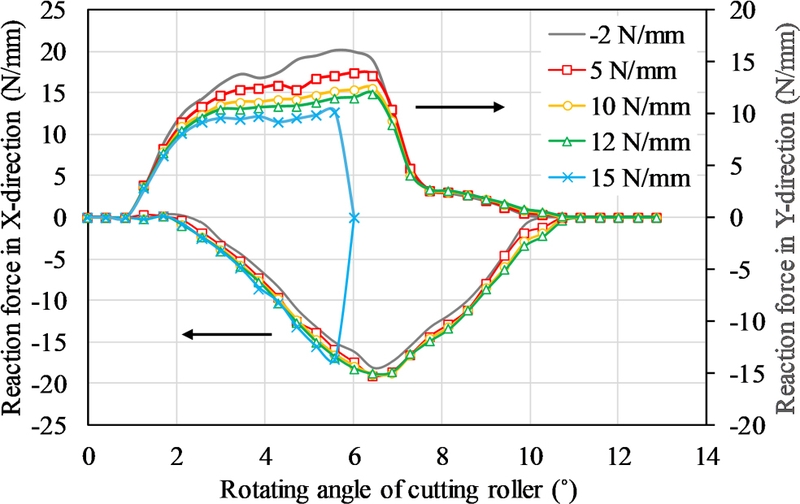
필름장력은 롤투롤 공정에서 주요 변동요인으로 작용하므로, 이에 따른 영향을 해석하였다. 단위 두께당 장력은 -2(압축)에서 15 N/mm(인장)까지 증가하는 조건을 설정하였다. Fig. 12에 장력 변화에 따른 작용력의 결과를 나타내었다.

Fig. 12

Variation of reaction force with rotating angle of cutting roller at different surface tractions

분석결과, X 방향 커팅 힘에는 장력의 영향이 매우 미미한 반면, Y 방향 커팅 하중은 장력이 증가할수록 감소하는 경향을 보였다. 이는 장력 증가로 인해 필름에 가해지는 Pre-stress가 압입 저항을 줄인 결과로 해석할 수 있다. 장력이 과도하게 높아질 경우(15 N/mm), 작용력이 낮아지면서 잔류 두께 부위에서 큰 변형이 발생하였다. 이로 인해 필름이 분리되면서 작용력이 0으로 되는 현상이 나타났다. 이러한 결과를 통해 장력 변화가 커팅 힘과 커팅 깊이 변화가 민감하게 작용한다는 것을 확인할 수 있었다.

3.2.3.2 필름 이송속도 변동

필름 이송속도는 필름 장력과 함께 롤투롤 공정의 주요 변동 요인으로 작용한다. 서포터 롤러의 표면선속 및 칼날 끝단의 회 전선속과 동일한 기준 필름속도(V_f) 100 mm/s에서 속도가 -0.8%에서 0.8%까지 변동할 때 반작용력의 변화를 Fig. 13에 나타내었다.

Fig. 13

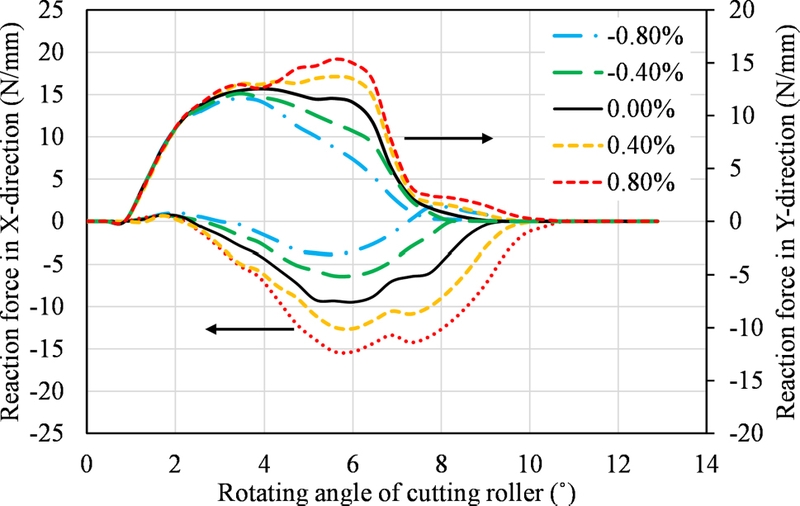
Variation of reaction force with rotating angle of cutting roller at different errors of film velocity

필름의 속도가 기준값보다 증가하면 힘의 X 방향 반작용력이 뚜렷히 증가하며, Y 방향 반작용력도 커팅 롤러 회전각도 4^o-7^o 회전각도 구간에서 증가한다. 반대로 필름속도가 감소하면 반작용력 역시 감소하는 경향을 보인다. 그러나 필름속도가 0.8% 수준으로 감소할 경우, 롤러 회전각도 8^o 부근에서 X 방향 힘이 음(-)에서 양(+)으로 역전되는 현상이 발생하므로 이는 공정상 바람직하지 않은 결과로 생각된다.

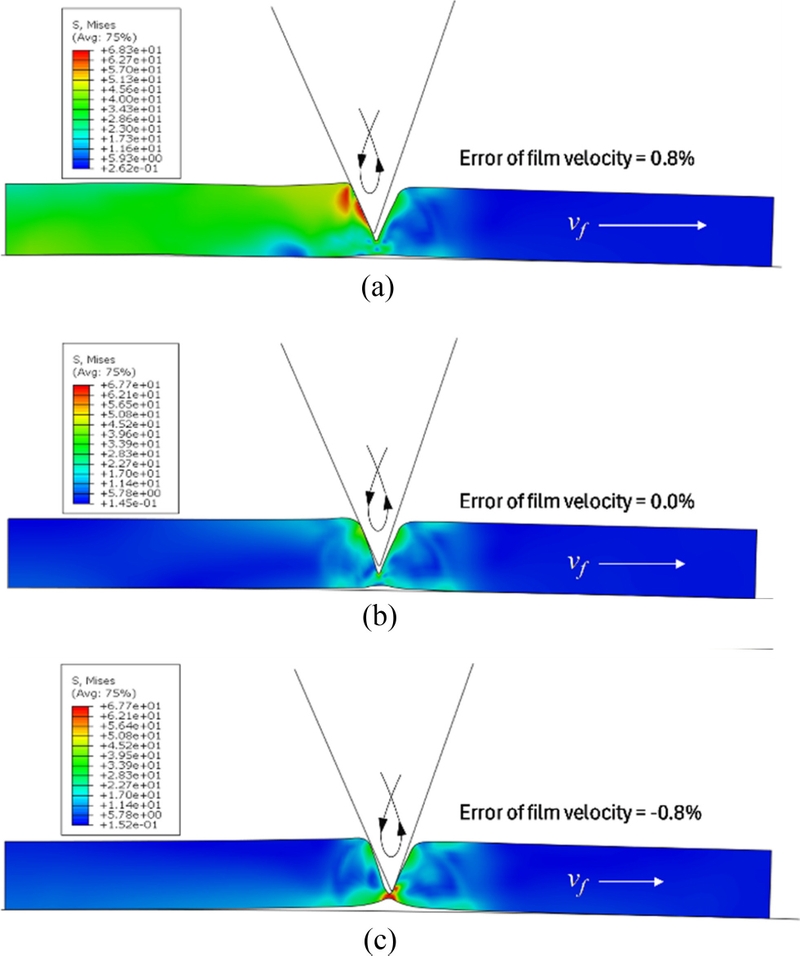
이러한 필름 속도에 따른 힘의 차이는 퇴거 중인 칼날 (커팅롤러 회전각도 8.6^o) 주변에서 발생하는 필름의 응력 분포 차이를 통해 확인할 수 있다. Fig. 14(a)는 필름 속도가 기준값보다 비해 빠를 때(필름속도오차 0.8%)를 나타내며, 칼날의 왼쪽에서 필름에 큰 응력이 발달되어 있음을 보여준다. 이는 칼날이 왼쪽 상단으로 퇴거하면서 필름에 밀착되어 X 방향의 힘이 크게 나타난 원인으로 해석된다.

Fig. 14

von-Mises stress distribution under film velocity errors of 0.8% (a), 0.0% (b), and -0.8% (c)

Fig. 14(b)는 기준속도로 필름이 이송될 때를 나타내며, 이 경 우 필름 왼쪽의 응력이 완화되어 힘이 감소한 모습을 확인할 수 있다. Fig. 14(c)는 필름 속도 오차가 -0.8%일 때로, 퇴거 중인 칼날 선단이 필름의 오른쪽 하단과 간섭되는 모습을 보여준다. 이 때문에 짧은 구간동안 (+)방향의 커팅롤러 반작용이 발생한다. 이러한 힘의 방향 전환은 커팅 공정 중에 동적 불안정성을 초래할 수 있는 요인으로 작용할 수 있다.

4. 결론

본 연구는 로터리 다이 커팅 공정에서 단층 PET 필름의 가공 과정에 대한 역학적 특성을 이해하기 위해 평면 모델을 기반으로 외연적 해석법을 적용하여 준정적 평면 응력 해석을 수행하였다. 로터리 커팅 모델링에 앞서, 수직 커팅 모델 해석을 통해 힘-변위 데이터를 실험 결과와 비교하였으며, 이를 기반으로 해석 모델의 타당성을 확인하였다. 적응형 메시를 설정하여 대변형 조건에서도 신뢰할 수 있는 결과를 얻었고, 해석결과의 안정성을 확인하였다. 해석 결과와 실험 결과의 근사성을 높이도록 칼날 표면과 필름 간의 마찰계수(μ_b = 0.2)와 서포트 롤러 표면과 필름 간의 마찰계수(μ_s = 0.3)를 설정하였다.

로터리 커팅 과정에서 필름의 변형 및 파단은 수직 커팅과 유사하게 길이방향 인장에 의해 지배되지만, 칼날 끝의 궤적에 의해 좌우 비대칭적 응력이 발생하고 필름 진행방향의 커팅 힘의 생성된다. 선단각에 따라 응력특성이 달라지는데, 작은 선단 각(25^o)의 경우 칼날 선단하부의 인장응력이 지배적인 반면, 큰 선단각(55^o)에서는 칼날 경사면에 의한 압축응력이 크게 발달하였다.

칼날의 선단각(α) 25^o-60^o 범위에서 선단각에 따른 최대 커팅힘은 선형적으로 변화하며, α = 40^o를 기준으로 그 기울기가 달라졌다.

단위 두께당 필름장력을 -2에서 15 N/mm까지 변동시킨 결과, 장력이 증가할수록 두께 방향 커팅 힘이 감소하였으나 길이 방향 힘에는 거의 영향을 미치지 않았다.

또한 필름과 칼날의 상대 속도 편차는 중요한 영향을 미쳤다. 기준 이송 속도에서는 칼날 좌우의 응력 편차가 작고, 퇴거 시 간섭이 없다. 반면, 이송 속도가 빨라지면 필름이 칼날을 밀어 두께 및 진행 방향 모두에서 커팅 힘이 증가하였다. 이송 속도가 기준 속도보다 0.8% 늦은 경우 칼날-재료간 접촉이 감소하여 두께 방향 커팅 힘이 기준 대비 50% 미만으로 감소하고 길이 방향 힘도 발생 후 즉시 감소하였다. 그러나 칼날 퇴거 과정에서 역방향 간섭이 발생하여 작용 하중의 방향이 변동될 가능성이 확인되었다. 현 조건에서는 기준 속도보다 약 0.4% 느린 속도가 절단 저항을 최소화하였다.

본 연구는 디스플레이 필름 등의 생산공정에서 품질과 생산성을 향상시키기 위한 목적으로 로터리 커팅 공정의 시뮬레이션 모델을 제시하였고, 칼날의 선단각, 장력, 속도와 같은 설계 및 공정 변수의 영향을 분석하였다. 이후에는 시뮬레이션 결과를 롤투롤 시스템 실제 장비에 적용하여 직접적인 커팅 힘의 측정 및 인자 평가 등 테스트 검증이 필요하다.

Acknowledgments

본 연구는 2022년 산업통상자원부의 기술개발사업(No. 1415185629) 및 교육부의 재원으로 한국연구재단의 지원(No. NRF-2018R1D1A1B07050525)을 받아 수행된 연구임.

REFERENCES

• Kim, D. W., Kim, S. W., Lee, G., Yoon, J., Kim, S., Hong, J.-H., Jo, S.-C., Jeong, U., (2023), Fabrication of practical deformable displays: Advances and challenges, Light: Science & Applications, 12(1), 61. [https://doi.org/10.1038/s41377-023-01089-3]
• Chae, Y., Chae, G., Youn, Y., Woo, S., Shin, S., Lee, J., (2018), Optimal design of thickness and Young’s modulus of multilayered foldable structure considering bending stress, neutral plane and delamination under 2.5 mm radius of curvature, International Journal of Precision Engineering and Manufacturing, 19, 1143-1154. [https://doi.org/10.1007/s12541-018-0135-7]
• Salmon, F., Everaerts, A., Campbell, C., Pennington, B., Erdogan-Haug, B., Caldwell, G., (2017), 64-1: Modeling the mechanical performance of a foldable display panel bonded by 3m optically clear adhesives, SID Symposium Digest of Technical Papers, 938-941. [https://doi.org/10.1002/sdtp.11796]
• Ha, M.-H., Choi, J.-K., Park, B.-M., Han, K.-Y., (2021), Highly flexible cover window using ultra-thin glass for foldable displays, Journal of Mechanical Science and Technology, 35, 661-668. [https://doi.org/10.1007/s12206-021-0126-y]
• Kim, M.-W., Ryu, K.-T., Kang, M.-C., (2013), Characteristics of tool wear and surface roughness using for hybrid lubrication in micro-milling process of flexible fine die, Journal of the Korean Society of Manufacturing Process Engineers, 12(6), 30-36. [https://doi.org/10.14775/ksmpe.2013.12.6.030]
• Ha, Y., Kim, M.-W., Kim, W.-B., (2023), A study on water contact angle and peel strength by anti-adhesion coating on die blade materials for adhesive film cutting, Tribology and Lubricants, 39(5), 190-196.
• Benedek, I., Feldstein, M. M., (2008), Technology of pressuresensitive adhesives and products, 1st edition, CRC Press. [https://doi.org/10.1201/9781420059410]
• Hoffmann, H., Schweitzer, M., Milberg, J., (1999), Rotary blanking, CIRP Annals, 48(1), 213-216. [https://doi.org/10.1016/S0007-8506(07)63168-0]
• Kirwan, M. J., (2012), Handbook of paper and paperboard packaging technology, John Wiley & Sons. [https://doi.org/10.1002/9781118470930]
• Liedert, C., Rannaste, L., Kokkonen, A., Huttunen, O.-H., Liedert, R., Hiltunen, J., Hakalahti, L., (2020), Roll-to-roll manufacturing of integrated immunodetection sensors, ACS sensors, 5(7), 2010-2017. [https://doi.org/10.1021/acssensors.0c00404]
• Jansson, E., Korhonen, A., Hietala, M., Kololuoma, T., (2020), Development of a full roll-to-roll manufacturing process of through-substrate vias with stretchable substrates enabling double-sided wearable electronics, The International Journal of Advanced Manufacturing Technology, 111, 3017-3027. [https://doi.org/10.1007/s00170-020-06324-4]
• Greener, J., Pearson, G., Cakmak, M., (2018), Roll-to-roll manufacturing: Process elements and recent advances, John Wiley & Sons. [https://doi.org/10.1002/9781119163824]
• Bollen, D., Deneir, J., Aernoudt, E., Muylle, W., (1989), Shear cutting of PET film, Journal of Mater Science, 24, 2957-2966. [https://doi.org/10.1007/BF02385653]
• Meehan, R. R., Burns, S., (1998), Mechanics of slitting and cutting webs, Experimental Mechanics, 38, 103-109. [https://doi.org/10.1007/BF02321652]
• Chaijit, S., Nagasawa, S., Fukuzawa, Y., Murayama, M., Katayama, I., (2006), Effect of tip profile on cutting processability of a trapezoidal cutting blade indented to an aluminum sheet, Journal of Mechanics of Materials and Structures, 1(8), 1301-1321. [https://doi.org/10.2140/jomms.2006.1.1301]
• Mitsomwang, P., Nagasawa, S., (2015), Effects of shearing parameters on cutting characteristics of polycarbonate sheet subjected to straight punch/die shearing, Journal of Materials Processing Technology, 220, 46-57. [https://doi.org/10.1016/j.jmatprotec.2015.01.007]
• Kaneko, S., Nagasawa, S., (2017), Estimation of wedge indentation resistance and plane compressive characteristics of acrylic PSA, Proceedings of the International Conference on Leading Edge Manufacturing in 21st century: LEM21 2017.9, 095. [https://doi.org/10.1299/jsmelem.2017.9.095]
• McCarthy, C. T., Annaidh, A. N., Gilchrist, M. D., (2010), On the sharpness of straight edge blades in cutting soft solids: Part II-analysis of blade geometry, Engineering Fracture Mechanics, 77(3), 437-451. [https://doi.org/10.1016/j.engfracmech.2009.10.003]
• McCarthy, C. T., Hussey, M., Gilchrist, M. D., (2007), On the sharpness of straight edge blades in cutting soft solids: Part Iindentation experiments, Engineering Fracture Mechanics, 74(14), 2205-2224. [https://doi.org/10.1016/j.engfracmech.2006.10.015]
• Popov, M., (2021), Prospects for the application of rotary cutting tools, Materials Today: Proceedings, 38, 1757-1759. [https://doi.org/10.1016/j.matpr.2020.08.254]
• Liu, C., Lu, H., Huang, Y., (2005), Dynamic steady-state stress field in a web during slitting, J. Appl. Mech., 72(2), 157-164. [https://doi.org/10.1115/1.1831298]
• Aggarwal, S., Bhushan, B., Katsube, N., (2005), Finite element analysis of the magnetic tape slitting process, Journal of materials processing technology, 166(2), 205-217. [https://doi.org/10.1016/j.jmatprotec.2004.08.014]