다구치 방법을 이용한 사출성형 미세유체 칩의 거시적/미시적 변형 거동에 대한 공정 변수의 영향 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This paper was presented at KSPE Autumn Conference in 2024
Abstract
Microfluidic chips have become a critical component in advanced applications such as biochemical analysis, medical diagnostics, drug development, and environmental monitoring because of their ability to precisely control fluid flow at the microscale. The functionality of these chips is highly dependent on the precision and dimensional stability of microchannel structures formed on them. While injection molding is an efficient method for a mass production of microfluidic chips, it is required to minimize undesirable deformation due to thermal and mechanical stresses, which can degrade the overall performance. This study investigated global (Macro-scale) and local (Micro-scale) deformation behaviors of injection-molded microfluidic chips. Effects of processing parameters, including mold temperature, melt temperature, filling time, and packing pressure, were investigated. The Taguchi-based design of experiments approach was employed to systematically analyze these effects and to determine optimal conditions to minimize deformation.
Keywords:
Injection molding, Microfluidic chip, Deformation behavior, Taguchi method, Processing parameter키워드:
사출성형, 미세유체 칩, 변형 거동, 다구치 방법, 공정 변수1. 서론
미세유체 칩(Microfluidic Chip)은 미세 유체역학을 기반으로 마이크로 스케일에서 유체의 흐름과 조작을 정밀하게 수행할 수 있는 소형 플랫폼이다[1]. 이 장치는 마이크로미터 크기의 채널과 구조가 집적된 형태로 제작되며, 물리, 화학, 생물학 등 다양한 분야에서 광범위하게 활용되고 있다[2,3]. 미세유체 칩은 유체의 흐름, 혼합, 분리, 분석 등의 과정을 정밀하게 수행할 수 있어, 질병 진단, 약물 개발, 환경 모니터링, 세포 연구 등 여러 응용 분야에서 중요한 역할을 한다[4,5]. 소형화, 경제성, 높은 정밀도, 신속한 처리 속도 등의 장점으로 기존의 대규모 실험장비를 대체할 수 있는 기술로 주목받고 있다[6]. 이러한 기술적 우수성 덕분에 랩-온-어-칩(Lab-on-a-chip)이라는 개념으로 발전하였으며, 이를 통해 단일 플랫폼에서 실험실 수준의 다양한 기능을 통합적으로 구현할 수 있다[7,8].
사출성형(Injection Molding) 공정은 미세유체 칩의 대량 생산과 정밀 제조를 실현하는 데 있어 핵심적인 역할을 한다. 이 공정은 열가소성 플라스틱을 금형(Mold)에 주입한 뒤 냉각과 고화 과정을 거쳐 원하는 형태의 제품을 제작하는 방식으로, 복잡한 구조를 정밀하게 구현할 수 있는 기술로 널리 인정받고 있다[9]. 사출성형은 대량 생산과 효율성 측면에서 뛰어난 장점을 제공하는 반면, 치수 안정성과 성능에 직접적인 영향을 미칠 수 있는 변형 문제가 발생할 수 있다[10]. 특히 미세유체 칩의 경우, 마이크로 채널의 정밀한 구조와 칩의 기능이 밀접하게 연관되어 있어 변형 문제는 제품 성능에 치명적인 영향을 줄 수 있다.
이와 같은 변형 문제를 해결하기 위해 다양한 연구가 진행되어 왔다. Chu 등은 인몰드 본딩(In-mold Bonding) 공정에서 열과 압력으로 발생하는 마이크로 채널 변형을 연구하여, 접합 온도와 압력을 조정하여 열팽창과 잔류응력을 감소시키고 구조적 정확성을 유지할 수 있음을 입증하였다[11]. Wang 등은 이형(Demolding) 공정에서 금형 인서트 설계와 표면 처리가 변형에 미치는 영향을 분석하여, 금형 표면 코팅과 냉각 시간 최적화를 통해 복제 품질을 향상시킬 수 있음을 보고하였다[12]. 또한, Attia 등은 미세 사출성형(Micro-injection Molding) 과정에서 재료의 유동성과 냉각 수축으로 인한 변형 문제를 해결하기 위해유동 시뮬레이션과 실험을 병행하여 사출 온도, 압력, 냉각 조건을 최적화하는 방법을 제안하였다[13]. 이러한 연구들은 공정단계별 변형 제어를 위한 유용한 데이터를 제공하였으나, 변형 메커니즘을 정량적으로 규명하고 공정 변수 변화가 변형에 미치는 영향을 체계적으로 분석한 사례는 여전히 부족하다.
본 연구는 이와 같은 한계를 보완하고자, 사출성형 공정을 통해 제조된 미세유체 칩에서 발생하는 변형 문제를 거시적(Macro) 및 미시적(Micro) 관점에서 함께 평가하고, 변형을 최소화하기 위한 최적의 공정 변수를 도출하는 데 초점을 맞추었다. 이는 변형 문제가 미세유체 칩의 전체적인 구조만이 아니라 마이크로 채널의 세부 기능에 미치는 영향을 종합적으로 이해하기 위함이다. 다구치 방법(Taguchi Method)을 활용하여 사출성형 공정 변수가 미세유체 칩의 각 변형에 미치는 영향을 체계적으로 분석하고, 변형을 최소화하기 위한 최적의 공정 변수를 도출함으로써 미세유체 칩의 제품 품질을 향상시키는 방안을 제시하였다.
2. 변형 해석 방법
2.1 미세유체 칩 모델
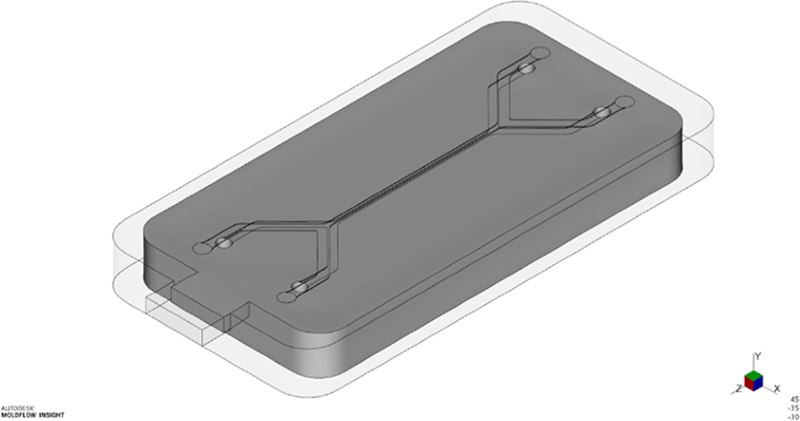
본 연구에서는 실제 사출성형 공정을 통해 제작된 미세유체 칩을 대상으로 변형 분석을 수행하였다. Fig. 1은 변형 분석의 주요 대상으로 선정된 미세유체 칩의 실제 사진을 보여준다. 이를 바탕으로, 사출성형 공정 중 발생하는 변형을 분석하기 위해 Fig. 2와 같이 미세유체 칩의 형상을 3D 모델로 설계하였다. 칩의 전체적인 치수는 길이 30 mm, 너비 15 mm, 두께 3 mm이며, 표면에는 깊이 0.04 mm인 Y형 교차 구조의 마이크로 채널이 설계되어 있다. 이때 게이트는 해석 모델에 포함하였으나, 스프루(Sprue) 및 러너(Runner)는 설계에서 제외하였다.
2.2 유한요소 설정
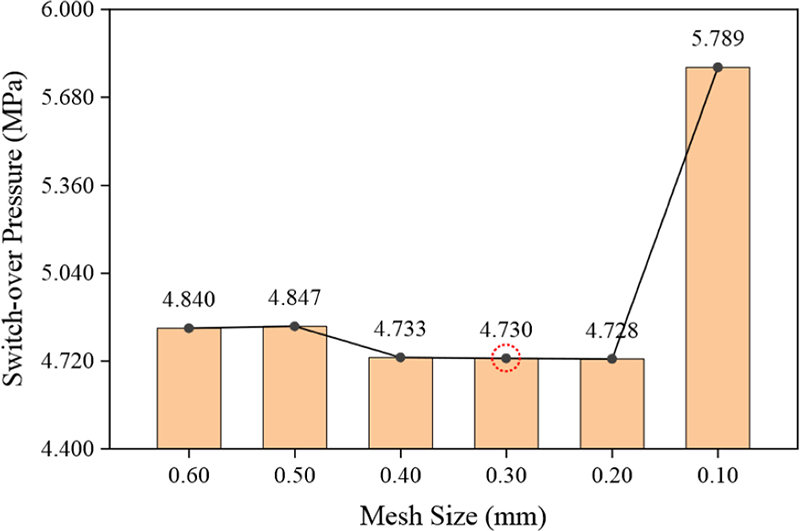
본 연구에서는 미세유체 칩의 변형을 분석하기 위해서 Moldflow Plastic Insight (MPI)를 사용하여 사출성형 해석을 진행하였다. 유한요소 해석 수행을 위해 메쉬 수렴성 테스트(Mesh Convergence)를 통해 적절한 메쉬 크기(Mesh Size)를 결정하였다. 실제 사출성형에 이용된 범용 폴리카보네이트(Generic Polycarbonate)의 권장 성형 조건을 기준으로 금형 온도(Mold Temperature)는 95oC, 용융 온도(Melt Temperature)는300oC로 설정하였고, 충전 시간(Filling Time)은 기본값인 1 s로 설정하여 테스트 공정 조건을 구성하였다. 이후 메쉬 크기를 0.60에서 0.10 mm까지 조정하며 보압 절환 압력(Switch-over Pressure)을 측정하였다.
Fig. 3과 같이, 메쉬 크기가 0.40에서 0.20 mm로 변하는 과정에서는 압력이 서서히 감소하며 수렴하는 경향을 보였다. 그러나 메쉬 크기를 0.10 mm로 설정한 경우, 압력이 급격하게 증가하는 현상이 관찰되다. 이는 과도하게 세밀한 메쉬 설정으로 인해 계산 과정에서 수치적 불안정성이 발생한 것으로 판단된다. 이러한 결과를 바탕으로, 계산 효율성과 결과의 신뢰성을 고려하여 메쉬 크기를 0.30 mm로 설정하였다.
최종적으로, Fig. 4와 같은 절점(Node) 수 89,286개, 요소(Element) 수 474,972개로 구성된 3차원 유한요소 모델을 구축하였다. 또한, 게이트 입구에 위치한 83개의 절점에 사출 주입구를 설정하여 캐비티 내 유동 해석의 안정성과 정확성을 확보하였다.
2.3 공정 변수 설정
본 연구에서는 미세유체 칩의 사출성형 품질과 특성에 영향을 미치는 주요 공정 변수로 충전 시간, 금형 온도, 용융 온도, 보압 압력(Packing Pressure)을 선정하였으며, Table 1과 같이 4요인 3수준의 공정 변수표를 구성하였다.
충전 시간(A)의 범위는 성형 품질에 미치는 영향을 고려하여 0.1-0.5 s로 설정하였다. 금형 온도(B)와 용융 온도(C)는 연구에서 가정한 범용 폴리카보네이트 소재의 권장 성형 온도 범위를 기준으로 각각 70-120oC, 280-320oC로 설정하였다. 보압 압력(D)은 공정 변수 조합에 따라 변하는 사출 압력에 대해서 최소한의 보압 효과를 보장하기 위해, 보압 절환 압력을 기준으로 하는 백분율 값인 100-200%로 설정하였다.
다른 공정 변수 중 보압 시간(Packing Time)의 경우, 기초 해석을 통하여 보압 시간이 6 s 이상일 경우 질량 변화가 발생하지 않음을 확인하였다. 따라서 본 해석에서는 보압 시간을 6 s로 고정하였다. 냉각 시간(Cooling Time)의 경우 별도의 냉각 시스템이 없으므로, 기본값인 15 s를 유지하여 해석을 진행하였다.
2.4 실험설계 및 보압 절환 압력 해석
다구치 방법은 제품 품질 향상 및 공정 최적화를 위해 널리 사용되는 통계적 기법으로[14], 실험의 효율성을 높이고 변동을 최소화하기 위한 강건 설계(Robust Design) 개념을 기반으로 한다. 제어요인(Control Factors)이 응답 변수(Response Variable)에 미치는 영향을 평가하여 최적 조건을 도출하며, 신호 대 잡음비(Signal-to-noise Ratio, S/N Ratio)를 활용해 품질 특성을 정량적으로 분석하는 것이 특징이다. 또한, 실험 횟수를 최소화하면서도 요인들의 영향을 체계적으로 평가할 수 있도록 직교배열표(Orthogonal Array)를 적용한다. 본 연구에서는 가장 많이 사용되는 L9(34) 직교배열표를 활용하여 공정 조건 조합을 구성하고, 사출성형 시뮬레이션을 수행하였다.
보압 절환 압력(Ps)은 사출성형 과정에서 충전이 99%에 도달하는 시점에 측정된 충전 단계에서 보압 단계로 전환되는 순간의 주입구에서의 압력이다. A(충전 시간), B(금형 온도), C(용융온도)를 변수로 설정하여 L9(34) 직교배열을 기반으로 유동 해석을 진행하였으며, 보압 절환 압력의 범위는 4.822-22.412 MPa로 나타났다. 최종적으로, 측정된 보압 절환 압력을 바탕으로 최소한의 보압 효과를 보장하는 D(보압 압력)를 산출하였으며, Table 2의 공정변수 조합을 이후 진행될 변형 해석에 활용하였다.
실험과 달리 수치 해석은 동일한 공정조건에서 항상 일정한 결과를 도출하므로, 일반적인 다구치 방법과는 달리 반응 값 자체를 활용하고 신호 대 잡음비는 따로 계산하지 않았다. 또한 4요인 3수준 공정변수에 L9(34) 직교배열을 적용하면 표본이 9개로 제한되므로, 분산분석(ANOVA)에서 공정 변수 간 상호작용은 포함하지 않았다.
2.5 변형 측정
본 연구에서는 미세유체 칩의 변형을 거시적 관점과 미시적 관점으로 나누어 분석하였다. 거시적 변형은 미세유체 칩의 전체적인 외형의 변형으로, 미시적 변형은 미세유체 칩 표면에 형성된 마이크로 채널의 변형으로 정의하고 각각에 적합한 평가 기준을 설정하였다.
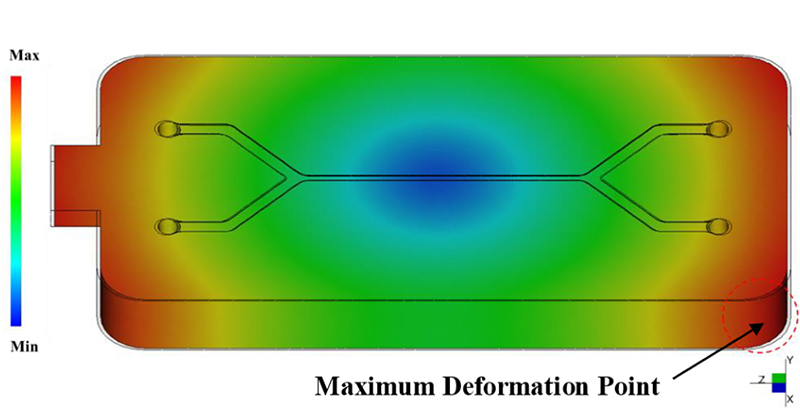
거시적 변형 평가는 칩에서 최대 변형이 발생하는 지점을 측정하는 방식으로 진행하였다. Fig. 5에 나타난 바와 같이 게이트로부터 가장 먼 모서리 중심부에서 최대 변형이 관찰되었으며, 이는 9가지 설계 조건 모두에서 일관된 결과를 보였다.
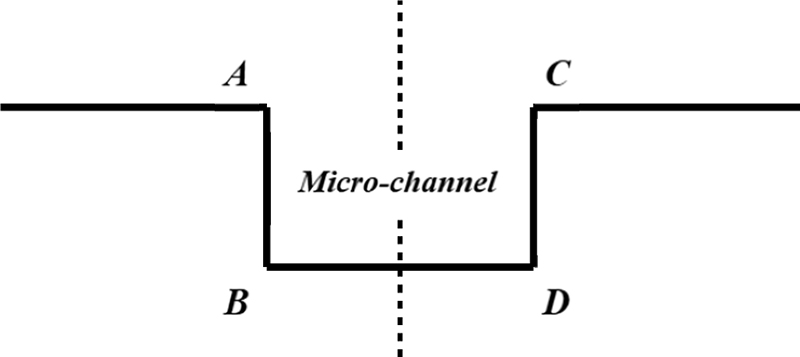
마이크로 채널의 미시적 변형 분석은 너비 0.3 mm의 중심부 채널을 대상으로 수행되었으며, 채널 단면을 사각형으로 가정하였다. 채널의 네 모서리의 점은 Fig. 6과 같이 각각 A, B, C, D로 명명하고, 채널의 길이 방향으로 일정 간격으로 정의된 8개의 지점에서 변형 양상을 평가하였다(Fig. 7). 마이크로 채널 변형의 정량적 분석을 위해서 부피 변형률(Volumetric Deformation Ratio)을 사용하였다. 마이크로 채널과 같은 육면체의 부피를 계산하기 위하여 다음식과 같이 각 위치의 8개 좌표점을 4개씩 조합하여 사면체 6개로 나누는 방식을 적용한다[15].
| (1) |
| (2) |
점 Pi(xi, yi, zi), Pj(xj, yj, zj), Pl(xl, yl, zl)은 사면체를 구성하는 각 꼭짓점 들의 3차원 좌표이며, V는 사면체의 부피를 나타낸다. 이때 1번과 2번 위치, 2번과 3번 위치처럼 인접한 위치들의 8점을 기반으로 모든 부피를 계산할 경우, 계산 과정이 매우 복잡해진다는 단점이 있다. 이러한 문제를 해결하기 위해, 채널 중심부를 기준으로 양끝 위치에 해당하는 1과 8번 측정 위치에서 8개 점(A1, B1,C1,D1,A8,B8,C8,D8)점을 활용하여 마이크로 채널의 부피를 계산하였다.
| (3) |
| (4) |
| (5) |
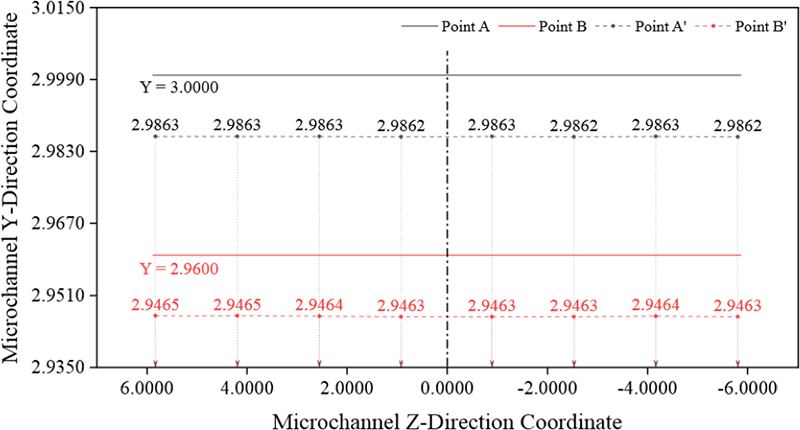
부피 변형률 (εV)을 사용한 해석 방법의 타당성 검증을 위해, 기준 조건(모든 공정변수가 2수준)에서 마이크로 채널 단면의 점 A와 B 지점의 Y, Z 좌표 변화를 측정하였다. Fig. 8의 측정결과에서 Z 좌표 위치에 따른 Y 좌표 변동이 대략 0.0001에서 0.0002 정도로 나타났다. 이는 μm 단위로 환산하더라도 미미한 수준에 해당하며, 해석 결과에 큰 영향을 미치지 않는 것으로 생각된다. 따라서 이러한 접근 방식이 계산을 단순화하고 시간 소요를 줄이면서 분석에 적합한 것으로 판단하였다.
3. 변형 해석 결과
3.1 거시적 변형 해석
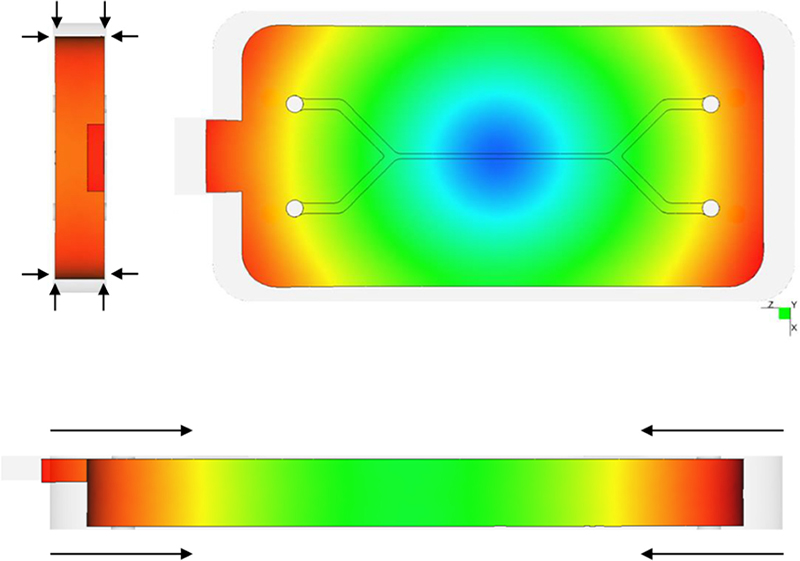
Fig. 9에 나타난 바와 같이, 미세유체 칩은 사출성형 후 전체적으로 초기 형상을 유지하면서 칩의 중심부를 향해 수축하는 변형경향을 보였다. 이 과정에서 휨 변형은 거의 발생하지 않았으며, X, Y, Z 세 방향 모두에서 수축이 관찰되었다. 사출성형에서 용융된 플라스틱 수지(Resin)는 금형에 주입된 후 냉각 및 고화 과정에서 부피가 줄어든다. 그러나 위치에 따라 냉각 속도가 균일하지 않기 때문에 변형이 일정한 방향성을 띠게 된다. 일반적으로 플라스틱은 온도가 낮아질수록 수축하는 특성을 가지며, 이 과정에서 외부와 내부의 냉각 속도 차이가 변형의 원인이 된다.
냉각은 금형과 맞닿은 외부에서 먼저 시작되며, 표면이 빠르게 고화됨에 따라 외부층이 먼저 수축한다. 반면, 내부는 상대적으로 늦게 냉각되면서 더 많은 수축이 진행된다. 하지만 외부는 이미 고화된 상태이므로 내부의 수축을 충분히 보상할 수 없으며, 결과적으로 내부 물질이 중심부 방향으로 끌려가면서 변형이 발생하게 된다.
Fig. 10에서 확인할 수 있듯이, 변형은 Z 방향(길이)에서 가장 크게 나타났으며, 그 다음으로 X 방향(너비), Y 방향(두께) 순으로 진행되었다. 이는 일반적인 사출성형 플라스틱 부품에서 흔히 관찰되는 변형 특성과 일치하며, 냉각 과정에서의 응력 분포에 영향을 받는다. 특히 Z 방향에서는 유동 경로가 가장 길어 온도 변화가 복잡하게 이루어지며, 유동 끝단에서는 상대적으로 낮은 온도에서 고화가 진행된다. 이로 인해 잔류응력이 축적되면서 Z 방향의 변형이 더욱 두드러지게 나타난다. 또한, 치수가 큰 방향일수록 냉각 시간 차이가 커지고 내부 응력 분포가 불균형해지면서 변형이 더욱 강조되는 경향을 보인다[16].
이와 같은 변형 패턴은 공정 변수에 따라 변형량의 차이는 있었으나, 실험에 사용된 9가지 설계 조건 모두에서 일관되게 나타났다.
Table 3의 거시적 변형 시뮬레이션 결과, 최대 변형값은 0.1702 mm, 최소 변형은 0.1506 mm로 확인되었다. 이를 바탕으로 변형을 최소화할 수 있는 최적의 공정 변수 조합을 도출하기 위해 다구치 방법의 절차에 따라 주효과도(Main Effect Plot) 분석과 분산분석을 진행하였으며, 각 공정 변수의 영향과 기여도를 평가하였다.
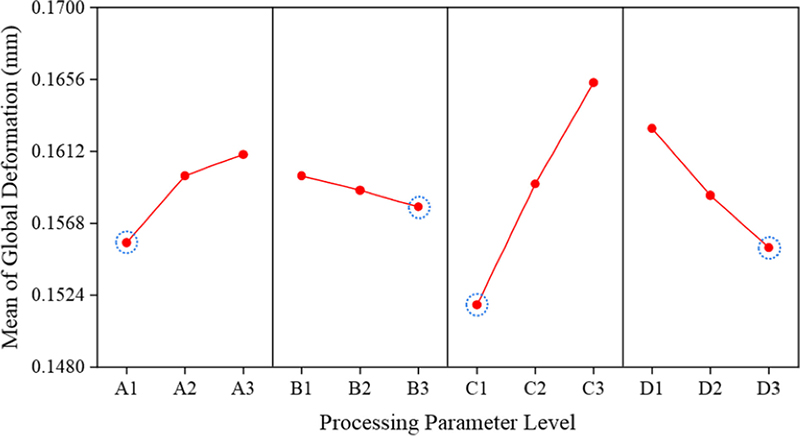
Fig. 11의 주효과도 분석 결과, C(용융 온도)가 가장 큰 영향을 미치는 변수로 나타났으며, 그 뒤를 이어 D(보압 압력), A(충전시간), B(금형 온도) 순으로 변형에 미치는 영향이 큰 것으로 확인되었다.
용융 온도(C)는 사출성형 공정에서 수지의 유동성과 응고 속도를 결정하는 가장 중요한 요소 중 하나로, 그 변화에 따라 제품의 수축률과 내부 응력이 크게 달라진다고 알려져 있다. 용융 온도의 수준이 낮을수록 변형이 감소하는 경향을 보였으며, 이는 용융 온도가 낮을 경우, 수지가 금형 내부에서 빠르게 응고하여 수축 시간이 단축되고 내부 응력이 균일하게 형성되어 변형이 억제되기 때문으로 해석된다. 그러나 용융 온도가 지나치게 낮으면 충전 불량 등의 문제가 발생할 수 있으므로, 변형 최소화를 위해 적절한 온도 조절이 필요하다.
보압 압력(D)은 증가할수록 변형이 감소하는 경향을 보였다. 이는 보압 압력이 높을수록 수지가 금형 벽면에 더욱 강하게 밀착되어 수축이 효과적으로 억제되기 때문으로 해석된다. 기존 연구에서도 보압 압력이 불충분할 경우, 재료 밀도가 균일하게 유지되지 않아 비대칭적인 수축이 발생하며, 이로 인해 제품 변형이 증가하는 경향이 보고된 바 있다[17]. 다만, 보압 압력이 과도하게 높아지면 내부 응력이 증가하여 오히려 제품의 품질에 부정적인 영향을 미칠 수 있으므로, 최적의 보압 압력 범위를 설정하는 것이 중요하다.
충전 시간(A)은 낮은 수준에서 변형이 감소하는 경향을 보였으며, 이는 재료가 금형 내에서 흐를 시간이 줄어들면서 내부응력의 비대칭적 분포가 완화되기 때문으로 해석된다. 반대로, 충전 시간이 길어질 경우 수지의 흐름이 불균일해지고, 특정 부위에서 과도한 응력이 발생하여 제품의 치수 정밀도가 저하될 수 있다고 보고된 바 있다[18]. 그러나 충전 시간이 너무 짧으면 충전이 불완전하게 이루어져 제품 내부에 결함이 발생할 가능성이 있으므로, 충전 시간을 적절하게 설정해야 한다.
금형 온도(B)가 높은 수준일수록 변형이 감소하는 경향을 보였으나, 다른 공정 변수들과 비교했을 때 변형에 미치는 영향은 상대적으로 적었다. 이는 금형 온도가 일정 수준 이상으로 설정되면 냉각 속도가 안정화되면서 수축 억제 효과가 포화 상태에 도달하여, 추가적인 온도 증가가 변형 저감에 미치는 영향이 크지 않기 때문으로 해석된다. 금형 온도가 너무 낮으면 불균일한 냉각으로 인해 수축 변형이 증가하지만, 일정 온도 이상에서는 변형 감소 효과가 저하된다고 보고된 바 있다[19].
분산분석 결과(Table 4)에 따르면, 용융 온도는 기여도가 67.39%로 가장 지배적인 영향을 미치는 변수로 확인되었다. 보압 압력의 기여도는 19.32%로, 변형 최소화에 있어 중요한 보조적 역할을 하는 것으로 나타났다. 충전 시간은 기여도가 11.84%로, 보압 압력의 절반 정도의 영향을 미쳤다. 반면, 금형온도는 기여도가 1.45%에 불과하여 거시적 변형 거동에 거의 영향을 미치지 않는 것으로 확인되었다. 이러한 분석 결과를 바탕으로 거시적 변형을 최소화하는 최적의 공정 변수 조합은 A1-B3-C1-D3으로 도출되었다. 해당 조합은 기존 초기 설계에 포함되지 않은 새로운 변수 조합으로 변형량은 0.1387 mm로 나타났다. 이는 기존 최대 변형값(0.1702 mm) 대비 18.51% 감소한 수준이며, 기존 최소 변형값(0.1506 mm)과 비교해도 7.9% 감소하여 변형 최소화 목표를 성공적으로 달성하였다.
3.2 미시적 변형 해석
마이크로 채널의 미시적 변형 전후의 좌표 분석 결과, 점 A, B, C, D는 모두 기본적으로 미세유체 칩의 중심 방향으로 이동하는 경향을 보였다. 특히 X 좌표에서 A와 C 지점의 변위가 B와 D 지점보다 더 크게 나타났으며, 이로 인해 단면이 Fig. 12와 같이 사다리꼴 형태로 변형되었다.
Y 좌표에서는 모든 지점이 하향 이동하는 경향이 관찰되는데, 이는 마이크로 채널이 칩의 중심선보다 상부에 위치하는 구조적 특성과 관련이 있다. 마이크로 채널의 깊이는 0.04 mm, 칩 전체 두께는 3mm로 설정되었으므로, 채널은 칩 중심선(1.5 mm)보다 위쪽에 존재한다. 사출 성형 공정에서 칩이 전반적으로 수축할 때, 상부에 위치한 채널은 중심선을 향해 움직이며, 이로 인해 Y 좌표 방향으로 하향 변위가 발생한다. 이와 같은 현상은칩 내부에서 균일하지 못한 온도 분포가 발생하고, 냉각 과정에서 수축량이 겉면과 내부가 다르게 나타나기 때문에 더욱 뚜렷하게 나타난다.
Z 좌표에서의 변위는 네 지점 모두에서 거의 동일한 수준을 보였고, 이에 따라 단면 전체가 평행하게 이동한 것으로 분석되었다. 이는 미세유체 칩의 냉각 시스템이 별도로 설정되지 않았고, 메쉬 구조가 Z 방향으로 대칭적이었기 때문으로 해석된다. 이는 사출 성형 과정에서 재료의 흐름이 Z 방향으로 균일하게 이루어졌음을 의미하며, 결과적으로 단면 전체가 동일한 방향으로 평행하게 이동하는 변형 거동을 초래하였다.
결과적으로, 위와 같은 미시적 변형 특성은 사출 성형 중 발생하는 온도 분포, 응력 분포, 그리고 채널의 구조적 위치 등이 복합적으로 상호 작용하여 나타나는 결과로 해석된다. 사출 성형 중 생기는 잔류응력은 마이크로 채널의 위치와 깊이에 따라 불균형적으로 형성되고, 이를 기반으로 채널 영역의 수축률이 주변 영역과 상이해진다. 또한 사출 압력과 보압 압력, 금형 온도, 냉각 속도 등 공정 변수들은 채널 부위에 걸리는 응력 분포와 열 전달(Heat Transfer)을 좌우하여, 마이크로 채널 단면의 변형양상을 결정하는 주요 요인이 된다.
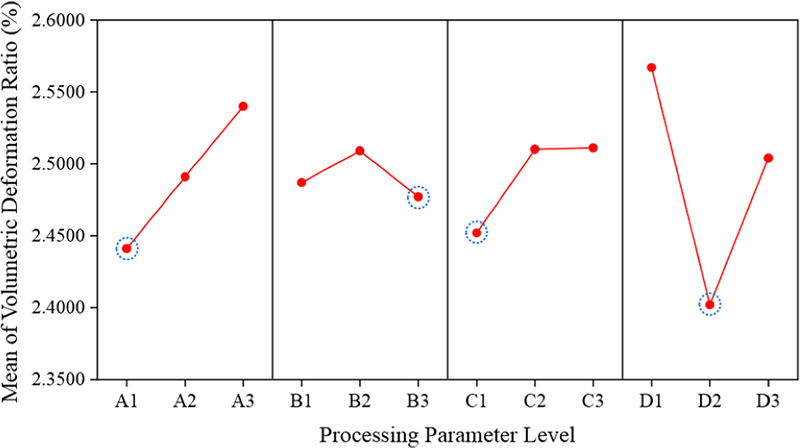
변형 전 마이크로 채널의 육면체 부피는 0.1410 mm3로 계산되었으며, 변형 후 부피는 4면체 6개의 부피 합으로 계산하였다. 이후 Table 5에 정리된 바와 같이 부피 변형률을 도출하였다. Fig. 13의 주효과도 분석 결과를 보면, 그래프의 기울기가 거시적 변형 결과를 전반적으로 반영하는 가운데 일부 공정 변수에서 상이한 특성을 보이는 것을 확인하였다. 충전 시간과 용융온도의 경우, 낮은 수준에서 변형이 감소되는 경향이 거시적 변형 결과와 유사한 것으로 나타났다.
금형 온도의 경우, 그래프 기울기가 증가하다가 다시 낮아지는 형태로 나타났으며, 중간 수준에서 변형이 최대가 되는 특징을 보인다. 이러한 비선형적 변화는 금형 온도가 일정 범위를 넘어가면 더 이상 냉각 효과가 지배적이지 않고, 대신 재료의 점도 변화나 유동성 개선이 주요 변수로 작용하기 때문으로 볼 수 있다. 결과적으로 중간 수준에서 금형 온도가 변형이 최대가 되었지만, 낮은 수준과 높은 수준만 비교하면 거시적 변형과 큰 차이를 보이지 않는다.
보압 압력에서는 기울기가 먼저 감소한 뒤 다시 증가하여, 중간 수준에서 변형량이 가장 낮게 나타나는 경향이 관찰된다. 이는 금형 온도와 달리 변형 최솟값이 중간 수준에서 나타나므로, 단순히 낮은 수준과 높은 수준을 비교하기 어렵다. 보압 압력이 과도하게 높으면 사출품 내부에 과다한 응력 축적이 발생할 수 있으며, 지나치게 낮으면 충분한 보압 작용이 이루어지지 않아 수축 공정의 균일성이 저해될 가능성이 크다. 이러한 결과는 주어진 공정 변수 범위에 의해 나타났을 가능성이 있으나, 마이크로 채널 변형을 최소화하기 위해서는 보압 압력의 적정값을 세밀하게 설정할 필요가 있다.
Table 6의 분석 결과에 따르면, 미시적 변형에 가장 큰 영향을 미치는 인자는 D(보압 압력)으로 기여도가 63.91%로 나타났으며, A(충전 시간)은 22.80%의 기여도로 두 번째로 큰 영향을 미치는 변수로 확인되었다. 이는 보압 압력이 마이크로 채널과 같은 미시적 변형을 제어하는 데 핵심적인 역할을 하며, 충전 시간 또한 변형의 발생에 중요한 영향을 미친다는 것을 보여준다.
이 결과는 마이크로 채널 구조가 매우 작은 잔류응력 변화에도 민감하게 반응하기 때문에, 보압 압력이 마이크로 채널의 형상 안정성과 잔류응력 제어에 결정적인 역할을 한다는 점과 일치한다[20]. 보압 압력은 보압 절환 압력과 밀접하게 연관되어 있으며, 이는 사출 압력과도 깊은 관계가 있다. 따라서 보압 압력과 관련된 충전 시간도 중요한 요소로 작용하며, 보압 압력과 충전 시간이 서로 상호 보완적으로 작용하는 결과를 나타낸다.
C(용융 온도)와 D(금형 온도)는 각각 10.84%와 2.44%의 기여도를 보여 상대적으로 낮은 영향력을 보였다. 미시적 변형에서 용융 온도의 기여도는 거시적 변형에 비해 상대적으로 감소한다. 이는 용융 온도가 물질의 유동성에 영향을 주긴 하지만, 미세 구조에서의 잔류응력 분포에는 보압 압력에 비해 덜 민감하다는 점을 의미한다. 금형 온도 역시 변형에 간접적으로 작용하는 변수로서, 주어진 조건 하에서는 변화 폭이 제한적이다. 다만 매우 정밀한 마이크로 채널 구조인 경우 국부 냉각 속도 및 응력 분포가 미세하게 달라질 수 있어, 필요에 따라 충전 시간 및 보압 압력과 함께 고려하여 조정하는 방안이 유효할 것으로 보인다[21].
미시적 변형의 최적 공정 변수 조합은 A1-B3-C1-D2로 나타났으며, 시뮬레이션 검증 결과, 이 조합에서의 부피 변형률은 2.2332%로 측정되었다. 이는 기존 최댓값인 2.6213% 대비 0.3881% 감소한 수치이며, 최솟값인 2.3492%와 비교했을 때도 0.1160% 더 감소하였다.
3.3 변형 최적화 검증
앞선 다구치 방법을 사용한 분석을 통해 거시적 변형과 미시적 변형을 각각 최소화하는 최적 공정변수 조합을 도출하였으며, 이를 통해 미세유체 칩 성형 시 변형이 응력과 밀접하게 연결되어 있음을 확인하였다. 그러나 이와 같은 최적 조건을 적용하더라도, 사출성형 공정 과정에서 발생하는 잔류응력(Residual Stress)이 재료의 항복응력을 초과할 경우 치명적인 치수 안정성 저하와 구조적 손상이 발생할 수 있다[25]. 이에 따라 도출된 최적 조건에서의 잔류응력을 분석하여, 실제 성형 과정에서 안전한 범위 내에 있는지 검증하고자 하였다.
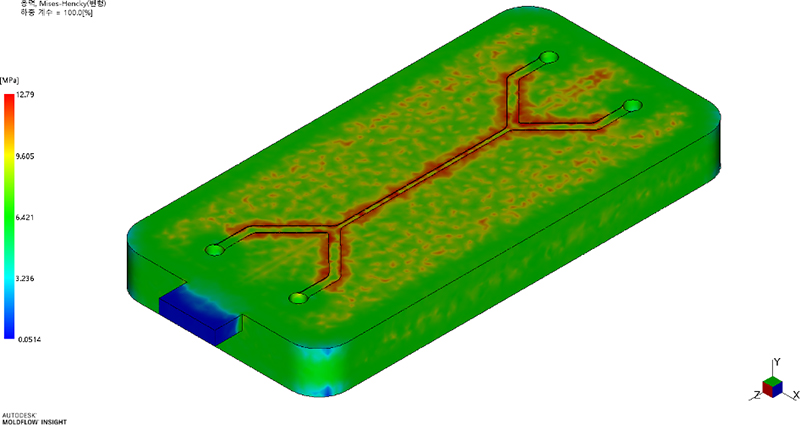
Table 7과 Fig. 14에 제시된 결과를 살펴보면, 잔류응력은 주로 마이크로 채널 주변에 집중되어 나타난다. 기준 조건(A2-B2-C2-D2)에서의 잔류응력 최대값은 12.790 MPa로, 폴리카보네이트의 항복응력(약 60 MPa)의 1/3 이하 수준임을 확인하였다. 이는 기준 조건이 재료 물성 범위 내에서 충분히 안전하게 성형될 수 있음을 시사한다. 거시적 변형 최소화 조건(A1-B3-C1-D3)을 적용했을 때는 잔류응력이 9.798 MPa로 나타나 기준 조건 대비 23.39% 감소하였으며, 마이크로 채널 변형 최소화 조건(A1-B3-C1-D2)에서는 9.230 MPa까지 낮아져 기준 조건보다 27.83% 감소하는 것으로 확인되었다.
결과적으로, 미시적 변형 최소화를 위한 조건이 거시적 변형 최소화 조건보다 잔류응력을 더 효과적으로 줄이는 것으로 나타났다. 이는 마이크로 채널의 변형을 감소시키는 최적화 접근이 성형 과정에서의 비대칭적 응력을 보다 균일하게 분산시켜 구조적 안정성과 정확도를 높일 수 있음을 의미한다. 미세유체 칩에서는 마이크로 채널의 구조적 정확도가 전체 성능에 직결되므로, 이러한 점을 고려할 때 마이크로 채널의 변형 최소화 조건(A1-B3-C1-D2)이 성능 향상 및 안정성 확보에 더욱 적합하다고 할 수 있다.
4. 결론
본 연구에서는 사출성형 미세유체 칩의 거시적 및 미시적 변형거동을 이해하고 공정 변수의 영향을 확인하기 위한 모델링 및 해석적 연구를 수행하였다. 이를 위하여 다구치방법을 사용하여 주요 공정변수들의 영향을 분석하고 변형을 최소화하는 공정변수 조합을 도출하였다. 이를 통하여 다음과 같은 주요 결과를 확인할 수 있었다.
- (1) 거시적 변형 해석 결과, 칩은 균일한 형상을 유지하면서 중심부를 기준으로 수축 변형이 발생하여 일반적인 사출성형제품에서 나타나는 경향과 유사한 결과를 보였다.
- (2) 주어진 공정 변수 범위에서 용융온도는 거시적 변형에 가장 큰 영향을 미치는 변수이며 67.39%의 높은 기여도를 갖는다. 용융 온도가 높아질수록 수지의 유동성이 증가하여 충전과 압축 단계에서 보다 균일한 응력 분포를 형성함으로써 변형이 감소하였다. 최적 공정조건은 A1-B3-C1-D3이고, 이때의 변형량은 0.1387 mm로 기존 시뮬레이션 데이터 대비 7.9-18.51%의 변형 감소를 달성하였다.
- (3) 미시적 변형 해석에서는 채널 단면이 사다리꼴 형태로 변화하며 평행 이동하는 양상이 관찰되었고, 채널 중심선에 가까워질수록 변형량이 감소하는 경향을 보였다.
- (4) 미시적 변형의 최적 공정 조건은 A1-B3-C1-D2로 부피 변형률이 2.2332%로 나타났으며, 기존 시뮬레이션 데이터 대비 0.1160-0.3881% 추가 감소를 확인하였다. 또한 보압 압력과 이에 직결되는 충전 시간은 마이크로 채널의 구조적 특성상 잔류응력 및 변형 결과에 큰 영향을 미치는 요인으로 분석되었다.
- (5) 금형 온도가 거시적 변형 및 마이크로 채널 변형에 미치는 영향은 각각 1.45%, 2.44%로 다른 공정 변수에 비해 기여도가 매우 낮았다.
- (6) 미시적 변형을 최소화하는 A1-B3-C1-D2 조건이 잔류응력을 더욱 효율적으로 줄여 구조적 안정성과 정확도를 높이는데 유리함을 확인하였다.
Acknowledgments
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. RS-2024-00357288).
REFERENCES
-
Ziółkowska, K., Stelmachowska, A., Kwapiszewski, R., Chudy, M., Dybko, A., (2013), Long-term three-dimensional cell culture and anticancer drug activity evaluation in a microfluidic chip, Biosensors and Bioelectronics, 40(1), 68-74.
[https://doi.org/10.1016/j.bios.2012.06.017]

-
Wu, J., He, Z., Chen, Q., Lin, J. M., (2016), Biochemical analysis on microfluidic chips, TrAC Trends in Analytical Chemistry, 80, 213-231.
[https://doi.org/10.1016/j.trac.2016.03.013]

-
Ren, K., Zhou, J., Wu, H., (2013), Materials for microfluidic chip fabrication, Accounts of Chemical Research, 46(11), 2396-2406.
[https://doi.org/10.1021/ar300314s]

-
Wang, X., Liu, Z., Fan, F., Hou, Ya., Yang, H., Meng, X., Zhang, Y., Ren, F., (2019), Microfluidic chip and its application in autophagy detection, TrAC Trends in Analytical Chemistry, 117, 300-315.
[https://doi.org/10.1016/j.trac.2019.05.043]

-
Fan, X. Y., Deng, Z. F., Yan, Y. Y., Shypko, A., Orel, V. E., Orel, V. B., Ivanova, D., Pilarsky, C., Tang, J., Chen, Z. S., Zhang, J. Y., (2022), Application of microfluidic chips in anticancer drug screening, Bosnian Journal of Basic Medical Sciences, 22(3), 302-314.
[https://doi.org/10.17305/bjbms.2021.6484]

-
Gao, H., Yan, C., Wu, W., Li, J., (2020), Application of microfluidic chip technology in food safety sensing, Sensors, 20(6), 1792.
[https://doi.org/10.3390/s20061792]

-
Guo, L., Feng, J., Fang, Z., Xu, J., Lu, X., (2015), Application of microfluidic “lab-on-a-chip” for the detection of mycotoxins in foods, Trends in Food Science & Technology, 46(2), 252-263.
[https://doi.org/10.1016/j.tifs.2015.09.005]

-
Özyurt, C., Uludağ, İ., İnce, B., Sezgintürk, M. K., (2023), Labon-a-chip systems for cancer biomarker diagnosis, Journal of Pharmaceutical and Biomedical Analysis, 226, 115266.
[https://doi.org/10.1016/j.jpba.2023.115266]

-
Su, C.-W., Su, W.-J., Cheng, F.-J., Liou, G.-Y., Hwang, S.-J., Peng, H.-S., Chu, H.-Y., (2022), Optimization process parameters and adaptive quality monitoring injection molding process for materials with different viscosity, Polymer Testing, 109, 107526.
[https://doi.org/10.1016/j.polymertesting.2022.107526]

-
Lan, X., Li, C., Yang, L., Xue, C., (2018), Deformation analysis and improvement method of the Ni-P mold core in the injection molding process, International Journal of Advanced Manufacturing Technology, 99, 2659-2668.
[https://doi.org/10.1007/s00170-018-2584-7]

-
Chu, C.-P., Jiang, B.-Y., Weng, C., Jiang, F.-Z., (2014), Microchannel deformation of polymer chip in in-mold bonding, International Polymer Processing, 29(2), 245-251.
[https://doi.org/10.3139/217.2845]

-
Wang Y, Weng C, Fei Z, Sun H, Jiang B., (2024), Enhancing structural replication of microfluidic chips: Parameter optimization and mold insert modification, Polymer Engineering & Science, 64(5), 2082-2095.
[https://doi.org/10.1002/pen.26675]

-
Attia, U. M., Marson, S., Alcock, J. R., (2009), Micro-injection moulding of polymer microfluidic devices, Microfluidics and Nanofluidics, 7, 1-28.
[https://doi.org/10.1007/s10404-009-0421-x]

-
Moayyedian, M., Abhary, K., Marian, R., (2018), Optimization of injection molding process based on fuzzy quality evaluation and Taguchi experimental design, CIRP Journal of Manufacturing Science and Technology, 21, 150-160.
[https://doi.org/10.1016/j.cirpj.2017.12.001]

-
Duczek, S., Duvigneau, F., Gabbert, U., (2016), The finite cell method for tetrahedral meshes, Finite Elements in Analysis and Design, 121, 18-32.
[https://doi.org/10.1016/j.finel.2016.07.004]

-
Azdast, T., Hasanzadeh, R., (2019), Experimental assessment and optimization of shrinkage behavior of injection molded polycarbonate parts, Materials Research Express, 6(11), 115334.
[https://doi.org/10.1088/2053-1591/ab4b19]

-
Otieno, S. O., Mwema, F. M., Mharakurwa, E. T., Jen, T. C., (2024), Fuzzy assessment of process parameter interactions on warpage defect modeling in plastic injection molding, International Journal on Interactive Design and Manufacturing, 1-14.
[https://doi.org/10.1007/s12008-024-02081-w]

-
Zhao, J., Cheng, G., (2016), An innovative surrogate-based searching method for reducing warpage and cycle time in injection molding, Advances in Polymer Technology, 35(3), 288-297.
[https://doi.org/10.1002/adv.21554]

-
Momeni, V., Hufnagl, M., Shahroodi, Z., Gonzalez-Gutierrez, J., Schuschnigg, S., Kukla, C., Holzer, C., (2023), Research progress on low-pressure powder injection molding, Materials, 16(1), 379.
[https://doi.org/10.3390/ma16010379]

-
Weng, C., Sun, H., Lai, J., Liu, J., Zhai, Z., (2021), Experimental investigation and molecular dynamics simulations of the effect of processing parameters on the filling quality of injection-molded micropillars, Polymer Engineering & Science, 61(10), 2427-2436.
[https://doi.org/10.1002/pen.25768]

-
Nian, S. C., Wu, C. Y., Huang, M. S., (2015), Warpage control of thin-walled injection molding using local mold temperatures, International Communications in Heat and Mass Transfer, 61, 102-110.
[https://doi.org/10.1016/j.icheatmasstransfer.2014.12.008]


M.S. candidate in the School of Mechanical Engineering, Chonnam National University. His research interest is polymer injection molding.
E-mail: parkji9694@gmail.com

Professor in the School of Mechanical Engineering, Chonnam National University. His research interests include multiscale polymer processing molding technologies and advanced nanocomposites.
E-mail: b.lee@chonnam.ac.kr