초고강도강 성형공정에서 소재산포에 의한 스프링백 경향

2.1 성형 CAE 조건

본 논문에서 고려한 제품은 Fig. 1에 도시한 차량용 프론트 루프 레일(Front Roof Rail)로 제품의 치수는 약 1128 mm × 174 mm × 62mm이다. 사용된 블랭크 소재는 인장강도 1 GPa급 초고강도강판인 SPFC980Y이며, 두께는 1 mm이다. 강판의 기계적 물성은 인장시험을 통하여 구하였으며, Table 1에 도시한 바와 같다. 블랭크의 항복거동을 모사하기 위하여 Hill의 평면 이방성을 고려한 1948 모델⁴을 사용하였고, 등방 경화모델(Isotropic Hardening Model)을 적용하였다. 블랭크의 형상 및 변형거동은 B-L-T (Beltschko-Lin-Tsay) 쉘요소⁵를 이용하여 모델링하였으며, 금형은 강체로 가정하였다.

Fig. 1

Shape of the front roof rail member

Table 1

Mechanical properties of SPFC980Y obtained from the tensile test

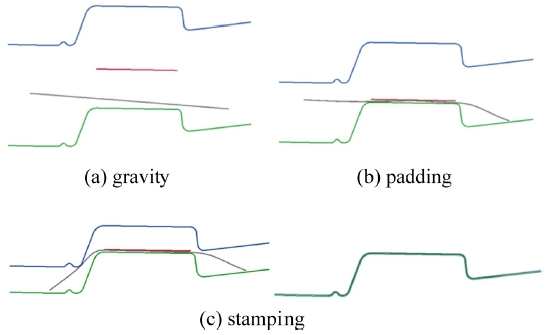
성형용 금형은 Fig. 2와 같이 다이, 패드, 펀치의 3개 부품로 구성되어 있으며, Fig. 3에 도시한 바와 같이 패드에 패딩력을 부과하여 블랭크를 고정한 후 상형이 하강하여 플랜지 부를 성형하는 방식으로 진행된다. 패딩력은 일정값인 224 kN을 부과하였으며, 상형의 하강속도는 1 m/s로 가하였다. 성형 CAE는 제1공정인 폼(Form) 타입 성형만을 대상으로 실시하였다. 하사점에서 블랭크 요소와 상하형 금형 간의 과도한 접촉에 의한 스프링백의 과소평가를 방지하기 위해 하사점 0.5 mm 전 까지 성형을 실시하고 스프링백 해석을 실시하였다. 성형 CAE는 상용 유한요소 프로그램인 Auto Form R6⁶를 이용하여 수행하였다.

Fig. 2

Finite element model of the stamping analysis

Fig. 3

Finite element model of the stamping analysis

2.2 성형 CAE 결과

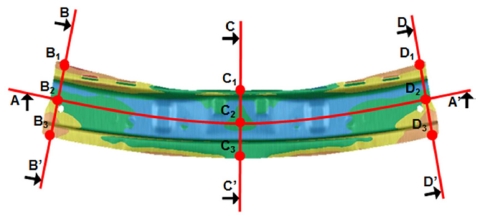
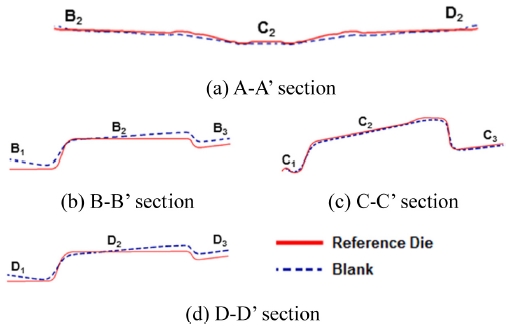
이상의 조건으로 해석을 실시한 후 스프링백 결과를 정량화하기 위하여 Fig. 4와 같이 길이 방향 스프링백 양(Camber)을 측정하기 위한 A-A’ 단면과 폭방향 스프링백을 측정하기 위한 B-B’, C-C’, D-D’ 단면을 설정하였다. 또한, 추후 스프링백 산포를 정량화하기 위한 측정점으로 폭방향 측정 단면에서 B₁-D₃로 명명한 9개의 지점을 설정하였다. 각 측정단면 및 측정점에서 금형면 기준으로 높이(z) 방향의 탄성 회복양을 측정하여 스프링백 정량화를 실시하였다. Fig. 5와 Table 2에 도시한 바와 같이 단면 A-A’에서 길이 방향 스프링백은 최대 1.15 mm가 발생하였으며, 단면 B-B’와 D-D’에서 최대 5.1 mm의 스프링백이 발생하고 있음을 확인하였다.

Fig. 4

Measurement sections and points for the quantification of the springback amounts

Fig. 5

Springback tendency in each section from the analysis results

Table 2

Amounts of springback in the measurement points

3.1 신뢰성 기반 최적화 기법

제 2절에서 수행한 성형공정 CAE는 소재 물성과 공정변수가 고정값으로 입력되어 해석의 결과도 고정값으로 도출되는 결정론적 해석방법(Deterministic CAE)으로 실제 성형 시에 발생하는 변수 산포 등의 외란 인자를 고려할 수 없다. 산포를 고려하기 위해서는 확률통계적 기법을 활용하여야 한다. 본 논문에서는 소재 물성과 공정변수의 산포에 의한 스프링백의 산포 경향을 정량화하기 위하여 신뢰성 기반 최적화 기법을 사용하였다. 본 기법은 입력변수의 불확실성을 고려하여 도출한 성능이 사용자가 원하는 수준의 수율을 만족하도록 하는 최적설계 기법이다.

3.2 산포분석 해석 조건

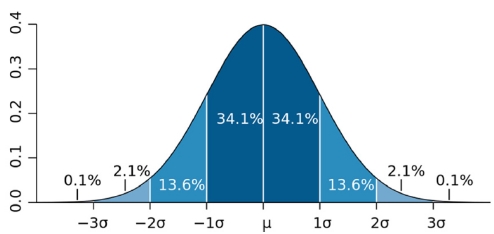
신뢰성 기반 최적화 기법을 적용하기 위하여 입력변수 중 산포를 고려할 대상을 선정하였다. 소재 물성에 관련된 변수는 블랭크 소재의 두께(t)와 인장강도(UTS) 및 항복강도(YS)이며, 공정변수는 쿨롱 마찰계수(μ)와 패딩력(PF)이다. 각 변수들의 산포 범위는 Fig. 6에 도시한 바와 같이 3 시그마(3-Sigma) 규칙⁷을 통해 부과하였다. 인장강도, 항복강도, 패딩력의 산포는 평균값 대비 10%를 부과하였으며, 두께 산포는 2%를 부과하였다. 실제 공정에서 제어가 가장 어려운 마찰계수의 산포량은 15%를 부과하였다. 각 변수에 부과한 평균값에 대한 최대 산포량을 Table 3에 도시하였다.

Fig. 6

Probability distribution of the design variable with the 3-sigma principle

Table 3

Amount of scattering for the design variables

선정된 5개의 공정변수들이 산포를 가질 때 제품의 스프링백에 많은 영향을 미치는 산포인자와 범위를 도출하고 산포 영향에 대한 스프링백 분포 결과를 정량화 하였다. 신뢰성 기반 최적화 기법은 상용 프로그램인 Auto Form-Sigma⁶를 이용하여 적용하였다. 결과값인 스프링백 양은 Fig. 4에 도시한 9개의 측정점에서 금형 형상 기준 높이방향의 탄성 회복량을 측정하여 활용하였다. 산포를 고려한 설계변수를 활용하여 96회의 성형해석을 실시하였으며, 성형해석에서 얻은 스프링백 값으로 메타 모델(Metal Model)을 구성하여 스프링백 산포량 예측에 활용한다.

3.3 스프링백 산포 기여도

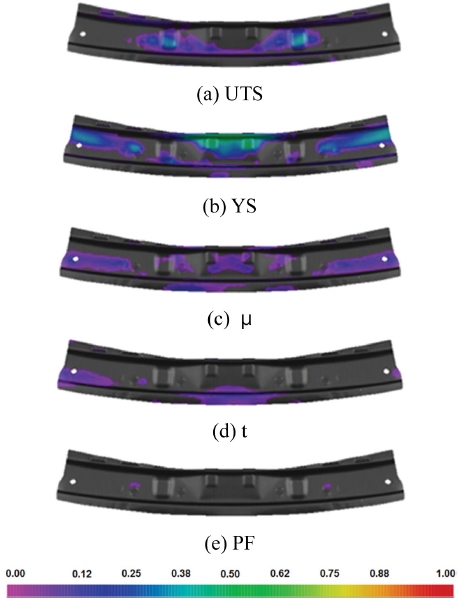
신뢰성 기반 최적화 기법을 활용하여 설계변수의 산포가 성형공정에서의 스프링백에 미치는 영향도를 분석하였다. 모든 변수의 산포를 고려한 경우 성형된 제품 위치에서의 각 설계변수가 스프링백에 미치는 영향도는 Fig. 7과 같다. 스프링백에 가장 큰 영향을 보인 변수는 항복강도, 인장강도, 마찰계수, 블랭크 두께 순으로 나타났고 패딩력의 영향은 미미하였다. 폼 성형 방식의 경우 굽힘변형이 주요 변형모드이므로 접촉과 마찰 등의 산포 보다는 소재 강도의 산포가 스프링백 산포 발생에 가장 중요한 인자로 볼 수 있다.

Fig. 7

Distribution of the contribution amounts of the design variables on the springback amounts

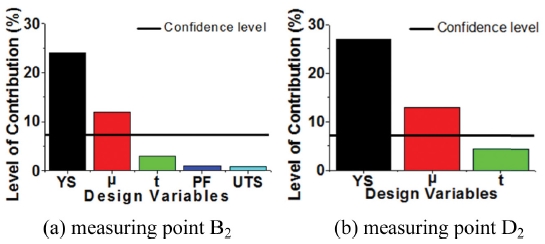
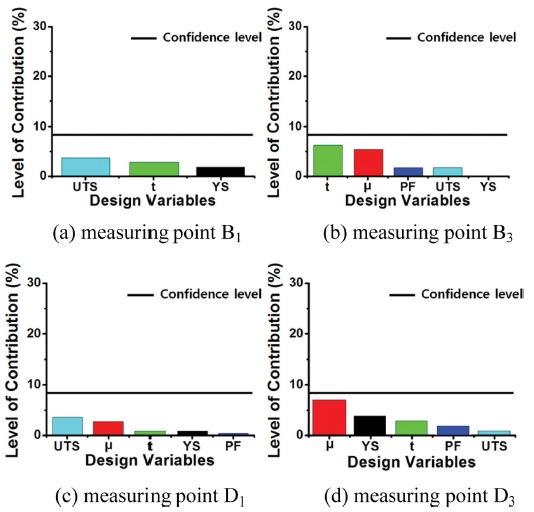
Fig. 8에 부품 길이방향 스프링백인 캠버(Camber) 양에 미치는 설계변수 기여도를 분석하였다. 측정점 B₂와 D₂에서 모든 설계변수 기여도의 합은 각각 40.9%와 44.3%로 나타나 유의성이 있음을 보였으며, 유의성이 있는 판단기준인 신뢰수준(Confidence Level)은 약 7%로 그보다 큰 값을 가지는 항복강도와 마찰계수가 스프링백 및 산포에 미치는 영향이 큼을 확인할 수 있었다. 두 측정점 모두 항복강도의 기여도가 25% 이상으로 나와 타 설계변수에 비하여 매우 큰 산포 기여도를 보였다. Fig. 9에 폭방향 스프링백 양에 미치는 변수 기여도를 분석하기 위하여 측정점 B₁, B₃, D₁, D₃에서의 기여도를 비교하였다. 캠버량과는 다르게 각 설계변수의 기여도가 크게 나오지 않았다.

Fig. 8

Contribution of design variable on the sprigback amount (camber)

Fig. 9

Contribution of design variable on the sprigback amount

3.4 스프링백 산포 정량화

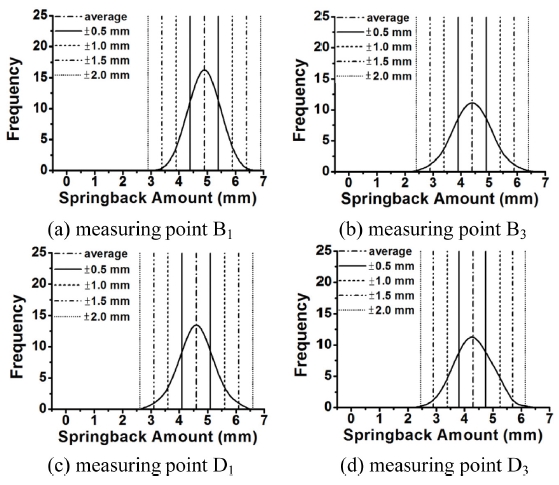
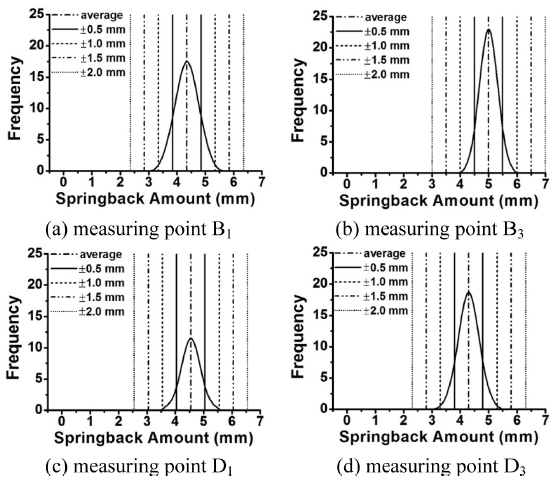
스프링백 양이 크게 나타나는 4개의 측정점 B₁, B₃, D₁, D₃에 대하여 항복강도가 스프링백에 미치는 영향을 정량화하였다. 먼저 5개의 설계변수의 산포영향을 고려한 분석을 수행한 결과를 Fig. 10과 Table 4에 도시하였다. 발생된 스프링백 평균값에서 ±0.5 mm의 공차범위를 만족하는 확률이 49.5% - 65.3%로 나타났다. 이는 결정론적인 해석에서 얻어지는 평균 스프링백 값에서 공차 1 mm를 벗어날 확률이 50% 정도가 됨을 의미하며, 일반 프레스 부품의 합격기준을 상회하는 수치를 보일 수도 있음을 보여준다. 스프링백 산포에 가장 큰 영향을 미치는 항복강도의 산포 영향을 정량화하기 위하여 항복강도의 산포를 고려하지 않고 산포분석을 실시하였다. Fig. 11과 Table 5에 도시한 바와 같이 스프링백 평균값에서 ±0.5 mm의 공차범위를 만족하는 확률이 80% - 90.2%로 나타남을 알 수 있다. 항복강도의 산포를 고려하였을 경우 표준편차가 0.571 - 0.701로 나오나 항복강도의 산포를 무시한 경우 0.316 - 0.407로 나타났다. 이는 항복강도에 의한 산포경향 증가가 매우 크다는 것을 확인시켜 준다. 일반적으로 성형금형 제작 및 양산 현장에서 블랭크 소재의 인장강도를 중점적으로 관리하는 데 반하여 산포의 관점에서는 항복강도의 관리가 매우 중요함을 의미한다.

Fig. 10

Probability plot considering scatters of the design variabless

Table 4

Probability distribution considering scatters of the design variables

Fig. 11

Probability plot considering scatters of the design variables except the yield strength (YS)

Table 5

Probability distribution considering scatters of the design variables except yield strength (YS)