외란관측기를 이용한 비선형 자기부상 시스템의 제어 성능 향상

1. 서론

자기부상 기술은 비접촉, 조용한 운전, 고효율 등의 장점을 가지고 있어 다양한 적용처에 사용되고 있다. 대표적으로 자기부상열차가 있고 자기 베어링도 분자 펌프와 칠러 등에 사용되고 있다[1,2].

자기부상 시스템(Magnetic Levitation System, MLS)은 전압을 통해 코일의 전류를 조절하고 자기력을 발생시켜 대상체의 위치를 제어하는 비선형 시스템이다[3]. 실제 MLS에 대상체 질량 등 시스템의 변화나 외란으로 인해 진동이 발생하거나 명령 추종 성능이 저하될 수 있어 제어 성능을 향상시키는 기술이 필요하다.

외란 관측기(Disturbance Observer, DOB)는 간단한 구조로 외란을 효과적으로 제거해줄 수 있다[4-6]. 하지만, MLS을 이용한 외란 제거와 명령 추종 성능 향상에 실험적 연구는 아직 많지 않고 대부분 상태공간 모델을 기반으로 연구하였다[7,8].

이 논문은 DOB를 이용한 MLS의 제어 성능 향상을 연구하였다. 먼저 MLS의 수학모델을 소개하고 주파수 응답 측정을 통하여 검증하였다. 물리 모델 기반으로 DOB를 설계하고 설계 변수에 따른 제어 성능 변화를 확인하였다. 또한, PID 제어로 부상된 MLS에 DOB를 적용하여 대상체 질량 및 외란 주파수 변화에 따른 외란 제거와 명령 추종 성능을 확인하였다. 마지막으로 폐루프 주파수 응답 측정을 통해서 DOB의 외란 제거 및 명령 추종 성능 향상 이유와 그 한계를 설명하였다.

2. 시스템 모델링

2.1 MLS

MLS는 대상체 (쇠공) 위치를 측정하고 전자석 코일 전압을 조절하여 부상시키는 비선형 시스템이다. MATLAB/Simulink와 연동하여 200 Hz 샘플링(Sampling) 주파수로 실시간 제어와 모니터링이 가능하다. Fig. 1에 사용한 MLS와 개략 모델을 나타냈다.

Fig. 1

MLS [9] (Adapted from Ref. 9 on the basis of webpage)

2.2 모델링

Eqs. (1)부터 (4)에 MLS의 비선형 수학 모델을 나타냈다. u는 전자석 코일 전압, m은 쇠공 질량, g는 중력 가속도, x₁은 쇠공 위치, x₂는 쇠공 속도, x₃은 전류, F_em은 전자기력, F_emP1은 코일 인덕턴스, F_emP2는 전자기력 관련 계수, k_i는 전류-전압의 정적 이득, f_i는 전자석 코일의 시상수이다.

$\[ {\dot{x}}_1=x_2 \]$

(1)

$\[ {\dot{x}}_2=-\frac{F_{em}}{m}+g \]$

(2)

$\[ {\dot{x}}_3=\frac{1}{f_i}\left(k_{i}u+c_i-x_3\right) \]$

(3)

$\[ F_{em}=x_3^2\frac{F_{em P1}}{F_{em P2}}exp\left(-\frac{x_1}{F_{em P2}}\right) \]$

(4)

위의 비선형 모델을 평형점 x₁ = 0.01 m에서 선형화하여 Eq. (5)에 나타냈다. A는 상태 형렬, B는 입력 행렬, C는 출력 행렬이다. MLS의 파라미터는 Table 1에 나타냈다.

$\[ \dot{x}=Ax+Bu,y=Cx \]$

(5)

Here, $$ A=\left[\begin{array}{ccc}0& 1& 0\\ a_{\mathrm{2,1}}& 0& a_{\mathrm{2,3}}\\ 0& 0& a_{\mathrm{3,3}}\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ b_3\end{array}\right],C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$$, $$ a_{\mathrm{2,1}}=\frac{x_{30}^2}{m}\frac{F_{em P1}}{F_{em P2}^2}\mathit{exp}\left(-\frac{x_{10}}{F_{em P2}}\right)$$, $$ a_{\mathrm{2,3}}=\frac{2x_{30}}{m}\frac{F_{em P1}}{F_{em P2}}exp\left(-\frac{x_{10}}{F_{emP2}}\right)$$, $$ a_{\mathrm{3,3}}=-f_i^{-1},\text{ and }{b}_3=k_i{f}_i^{-1}$$.

Table 1

Parameters of MLS

2.3 모델 검증

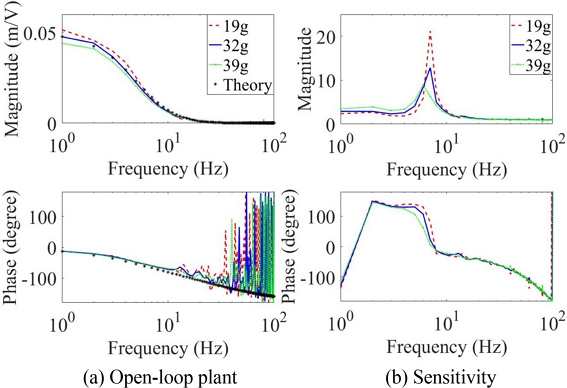
PID 위치 제어를 수행하면서 다중정현파(Multisine) 신호를 MLS에 부가하여 개루프와 폐루프 주파수 응답 측정을 하고 결과는 Fig. 2에 나타냈다. 우선 대상체 질량 변동에도 안정한 부상이 가능하도록 시행 착오를 통해 PID 제어 이득을 조절하였다. 질량을 19, 32, 39 g으로 변화시키면서 측정한 주파수 응답과 선형 이론 모델의 주파수 응답을 Fig. 2(a)에 나타냈다. 동작점에서 모델링의 정확도가 높고 대상체 질량 변화에 따라 1 Hz에서 주파수 응답 크기는 0.0476에서 0.0515 m/V로 약 8.19% 변화하였다. PID 제어로 부상시킨 대상체 질량 변화에 따른 민감도 함수를 측정하여 Fig. 2(b)에 나타냈다. 대상체 질량이 감소함에 따라 민감도함수의 최대값이 커져서 안정성이 줄어든다. 일반적으로 샘플링 주파수가 낮으면 자기부상 제어 성능이 떨어진다. 이 연구의 샘플링 주파수가 200 Hz로 낮아 대상체의 질량이 가벼움에도 변위 제어 절점 주파수가 7 Hz 정도로 낮고 제거 가능한 외란 주파수도 절점 주파수를 넘지 못한다.

Fig. 2

Open-loop frequency responses and closed-loop sensitivity functions of the MLS of different mass

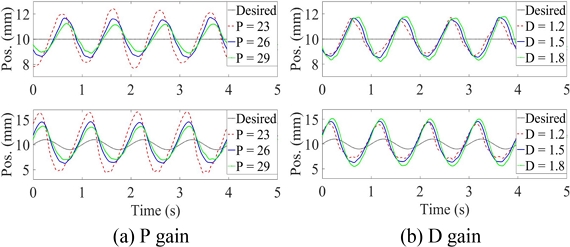
0.001 V 진폭의 정현파 외란과 0.01 m 진폭의 정현파 입력을 사용해 PID 제어기로 부상된 MLS의 외란 제거와 명령 추종 성능을 실험하여 Fig. 3에 나타냈다. Fig. 3(a)와 같이 비례 이득(P)이 증가할수록 외란 제거 성능과 명령 추종 성능이 향상된다. Fig. 3(b)를 보면 미분 이득(D)이 감소할수록 외란 제거 성능과 명령 추종 성능이 향상된다. 비례 이득이 증가시키고 미분 이득을 감소시키면 명령 추종 성능이 향상되나 MLS의 안정성이 나빠져 제어 이득 조절에 한계가 있다[10].

Fig. 3

Control performances of the MLS W/O DOB in cases of different PID gains (upper: disturbance rejection and lower: command following)

3. DOB

3.1 DOB 설계

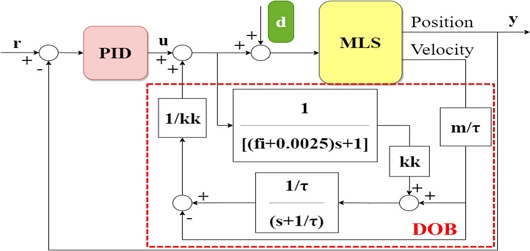
DOB는 기본적으로 동적 시스템의 외란을 추정하여 제거하며 DOB가 적용된 제어 시스템의 개략도를 Fig. 4에 나타냈다. 사용한 제어 시스템은 제어기(PID), 필터, 실제 플랜트(MLS)로 구성된다. 그리고 r, u, y는 각각 기준입력, 제어입력, 출력이며 d는 외란이다. kk는 전자석 구동기의 전압-힘 이득으로 Eq. (6)과 같다[11].

$\[ kk=m\times a_{\mathrm{2,3}}\times k_i \]$

(6)

Fig. 4

Schematic of the Simulink realtime block diagram of the MLS with DOB

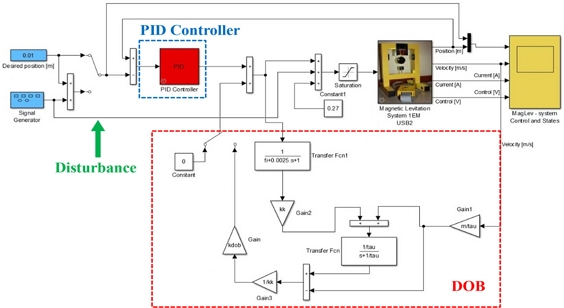
Fig. 5는 속도 피드백을 받는 DOB가 적용된 실제 제어 시스템의 블록 선도이다.

Fig. 5

Simulink realtime block diagram of the MLS with DOB

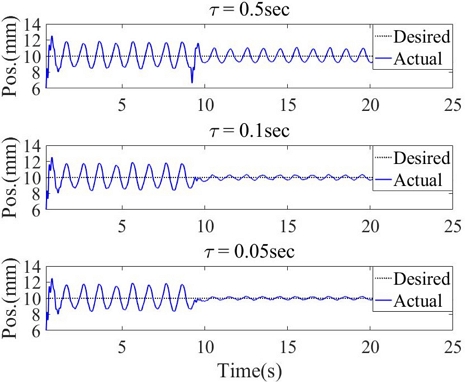
쇠공 질량 32 g, 외란 주파수 1 Hz일 때, 필터 시정수인 τ 변화에 따른 외란 제거 성능을 Fig. 6과 Table 2에 나타냈다. τ가 작아질수록 외란 제거 성능이 향상된다.

Fig. 6

Disturbance rejection of the MLS with DOB of different τ

Table 2

Disturbance rejection of the MLS with DOB of different τ

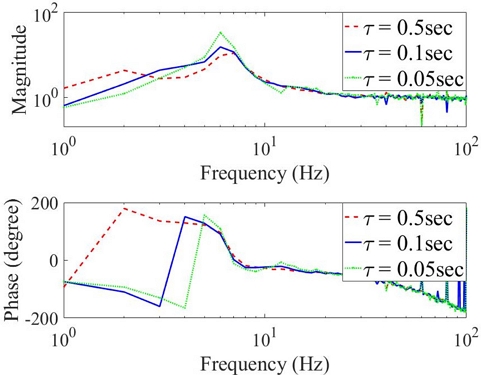
필터의 시정수 τ를 변화(0.5, 0.1, 0.05 sec)시키면서 실제 MLS의 폐루프 민감도 함수를 측정하여 Fig. 7에 나타냈다. τ가 감소하면 저주파 대역의 외란 제거 성능이 향상되지만 민감도 함수 최대값이 증가하여 안정성이 나빠진다.

Fig. 7

Sensitivity function of the MLS with DOB of different τ

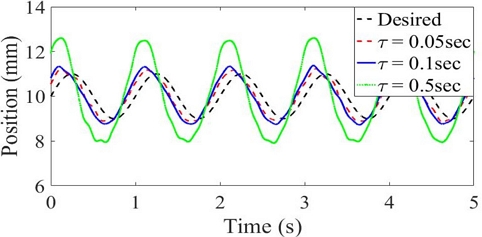
Q 필터의 시정수인 τ를 변화시키며 명령 추종 실험을 수행한 결과를 Fig. 8에 나타냈다. Q 필터의 시정수인 τ가 작을수록 명령 입력을 잘 추종한다.

Fig. 8

Command following of MLS with DOB of different τ

4. 실험

4.1 외란 제거 실험

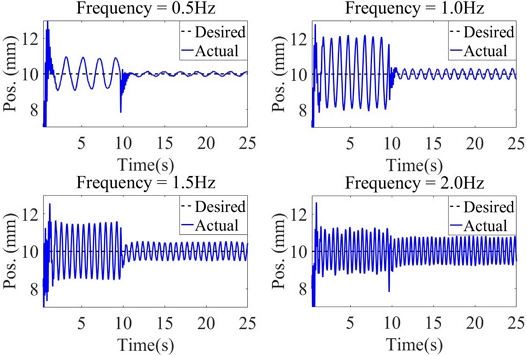
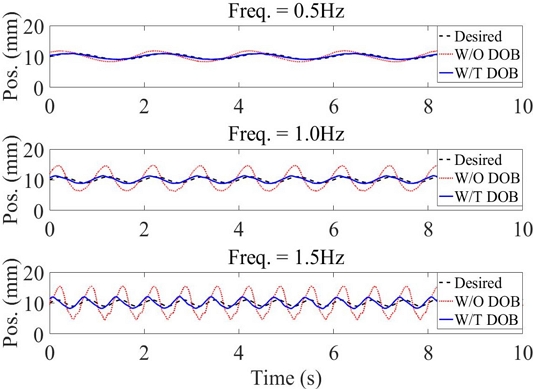
쇠공의 공칭 질량이 32 g이고 정현파 외란이 0.01 V(약 0.0184 N)일 때 외란 주파수 변화에 따른 외란 제거 응답을 Fig. 9와 Table 3에 나타냈다. 저주파 외란이 DOB로 잘 제거되지만 외란 주파수가 높아질수록 외란 제거 성능이 저하되었다. Table 3 과 같이 외란 주파수가 0.5 Hz일 때 약 83.6%, 주파수가 1 Hz 일 때 약 84.5%, 주파수가 1.5 Hz일 때 약 65.3%, 주파수가 2 Hz일 때 약 34.5%, 평균 67.0%로 제거되었다.

Fig. 9

Disturbance rejection of the MLS with DOB against different disturbance frequencies

Table 3

Disturbance rejection of the MLS against different frequencies

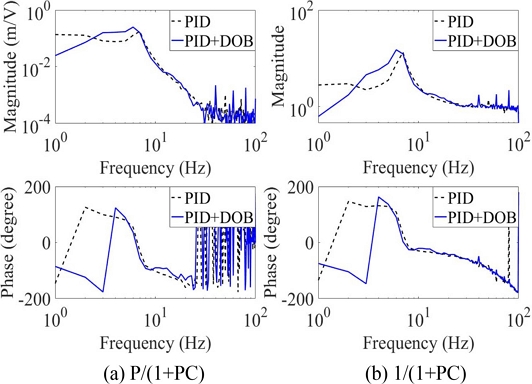
PID만 사용할 때와 PID 및 DOB를 같이 사용할 때의 MLS 폐루프 주파수 응답 측정한 결과는 Fig. 10(a)에 나타냈다. PID만 사용할 때보다 DOB를 같이 사용할 때 1-2.4 Hz 범위에서 외란 제거 성능이 향상되지만 2.4 HZ 이상의 주파수에서는 외란 제거 성능이 저하된다.

Fig. 10

Close-loop frequency responses of the MLS W/O and W/T DOB

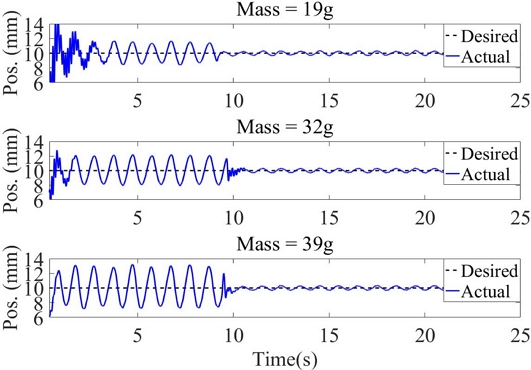
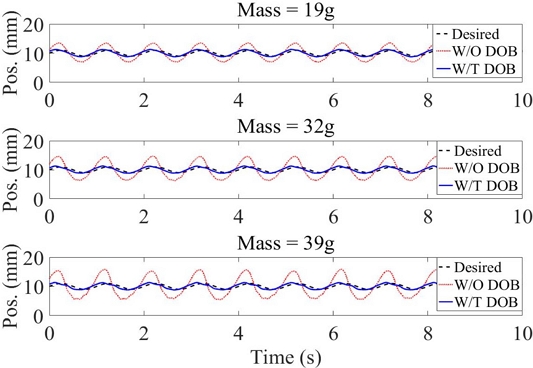
Fig. 11과 Table 4에 주파수가 1.0 Hz일 때 쇠공의 질량을 바꾸며 외란 제거 성능을 실험했다. 질량이 증가할수록 시스템 응답이 느려져 외란 제거 성능이 향상되었다. Table 4와 같이 외란 주파수가 1.0 Hz일 경우 쇠공 질량이 19 g일 때 약 79.9%, 질량이 32 g일 때 약 85.0%, 질량이 39 g일 때 약 90.3%, 평균 85.1%로 제거되었다.

Fig. 11

Disturbance rejection of the MLS of different masses W/T DOB

Table 4

Disturbance rejection of the MLS of different masses W/T DOB

4.2 명령 추종 실험

주파수 진폭이 0.001 m인 정현파 입력에 대한 명령 추종 실험을 수행했다. 쇠공의 질량이 32 g일 때 주파수 증가에 따른 명령추종 성능을 Fig. 12와 Table 5에 나타냈다. Table 5와 같이 DOB를 사용할 때 명령추종 성능이 평균 60.7% 향상되었다. 여기서 증폭비(Amp. Ratio)는 명령 응답과 명령의 비율이다.

Fig. 12

Command following of the MLS with DOB for different command frequencies (mass = 32 g)

Table 5

Command following of the MLS with DOB for different command frequencies (mass = 32 g)

주파수를 고정하고 쇠공의 질량 변화에 따른 명령 추종 실험을 수행하여 Fig. 13과 Table 6에 나타냈다. DOB를 사용하면 명령 추종 성능이 평균 68.6% 향상되며 질량이 증가할수록 응답이 느려져 더욱 향상되었다.

Fig. 13

Command following of the MLS of different masses W/T DOB (@1 Hz)

Table 6

Command following of the MLS of different masses W/T DOB (@1 Hz)

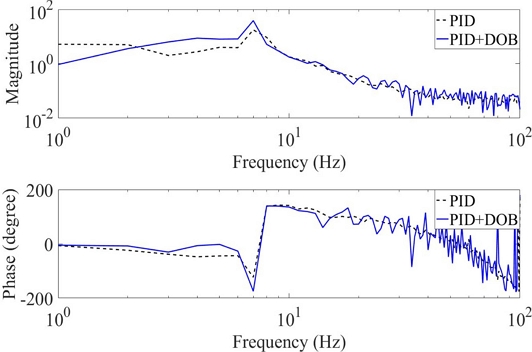
PID 제어기만 사용한 경우 PID 및 DOB를 함께 사용한 경우에 대해 상보 민감도 함수(PC/(1+PC))의 측정 결과를 Fig. 14에 나타냈다. 주파수가 2.2 Hz 이하에서 PID만 사용할 때보다 PID 및 DOB 같이 사용할 때 명령 추종 성능이 향상된다.

Fig. 14

Complementary sensitivity functions of the MLS W/O and W/T DOB

5. 결론

이 논문은 DOB를 이용한 MLS의 제어 성능 향상을 연구하였다. 물리 모델 기반으로 DOB를 설계하고 설계 변수 조절에 따른 제어 성능 변화를 확인하였다. DOB를 통해서 주파수가 2 Hz 이하에서 외란 제거 및 명령 추종 성능이 향상되었다. 외란 제거 성능은 평균 76.1%, 명령 추종 성능이 평균 64.7%로 향상되었다. 폐루프 주파수 응답 측정을 통하여 DOB의 성능 향상과 그 한계를 확인하였다. 향후 제어 시스템의 샘플링 주파수를 높이고 전류 제어를 포함한 MLS에 DOB를 적용하는 연구를 수행할 예정이다.

Acknowledgments

This paper was presented at KSPE Autumn Conference 2022

이 논문은 한국 에너지 기술평가원의 “수열 냉·난방 및 재생열 하이브리드 시스템 기술개발 및 실증”의 지원을 받아 연구되었음(No. 20208901010010, 2020).

REFERENCES

• Yang, Z.-J., Miyazaki, K., Kanae, S., Wada, K., (2004), Robust position control of a magnetic levitation system via dynamic surface control technique, IEEE Transactions on Industrial Electronics, 51(1), 26-34. [https://doi.org/10.1109/TIE.2003.822095]
• Yoo, S. J., Kim, S., Cho, K.-H., Ahn, H.-J., (2021), Data-driven self-sensing technique for active magnetic bearing, International Journal of Precision Engineering and Manufacturing, 22(6), 1031-1038. [https://doi.org/10.1007/s12541-021-00525-x]
• Balko, P., Rosinová, D., (2017), Modeling of magnetic levitation system, Proceedings of the 2017 International Conference on Process Control (PC), 252-257. [https://doi.org/10.1109/PC.2017.7976222]
• Radke, A., Gao, Z., (2006), A survey of state and disturbance observers for practitioners, Proceedings of the 2006 American Control Conference, 6. [https://doi.org/10.1109/ACC.2006.1657545]
• Shim, H., Park, G., Joo, Y., Back, J., Jo, N. H., (2016), Yet another tutorial of disturbance observer: Robust stabilization and recovery of nominal performance, Control Theory and Technology, 14(3), 237-249. [https://doi.org/10.1007/s11768-016-6006-9]
• Yamato, S., Nakanishi, K., Suzuki, N., Kakinuma, Y., (2021), Development of automatic chatter suppression system in parallel milling by real-time spindle speed control with observer-based chatter monitoring, International Journal of Precision Engineering and Manufacturing, 22, 227-240. [https://doi.org/10.1007/s12541-021-00469-2]
• Kang, N.-S., Jo, N.-H., (2013), A study on the controller design for EMS system using disturbance observer, The Transactions of the Korean Institute of Electrical Engineers, 62(9), 1264-1269. [https://doi.org/10.5370/KIEE.2013.62.9.1264]
• Jo, N.-H., (2022), A study on a reduced-order disturbance observer controller for nonlinear electro-magnetic suspension systems, Transactions of the Korean Institute of Electrical Engineers, 71(1), 196-202. [https://doi.org/10.5370/KIEE.2022.71.1.196]
• INTECO, Magnetic Levitation Systems. https://www.inteco.com.pl/products/magnetic-levitation-systems/
• White, M. T., Tomizuka, M., Smith, C., (2000), Improved track following in magnetic disk drives using a disturbance observer, IEEE/ASME Transactions on Mechatronics, 5(1), 3-11. [https://doi.org/10.1109/3516.828584]
• Kobayashi, H., Katsura, S., Ohnishi, K., (2007), An analysis of parameter variations of disturbance observer for motion control, IEEE Transactions on Industrial Electronics, 54(6), 3413-3421. [https://doi.org/10.1109/TIE.2007.905948]