코일전류 계산 및 AISI 1552 상변태를 고려한 주차기어의 고주파 열처리 시뮬레이션
1경상국립대학교 대학원 기계항공공학부Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study performed high-frequency heat treatment experiments and simulations of the park gear of an automobile transmission. The heating temperature and hardening depth were measured during high-frequency heat treatment. Moreover, by applying the resonance RCL circuit, the current value of the coil during high-frequency heat treatment, the electromagnetic and heat transfer material properties dependent on the temperature, and the phase transformation function were all applied to the simulation. In the high-frequency heat treatment experiment, the heating temperature was 977.4oC and the 1st direction hardening depth was 1.5 mm, the 2nd direction hardening depth was 3 mm, and the 3rd direction hardening depth was 2.5 mm, and the reliability was verified by comparing the simulation heating temperature of 1,097oC and the 1st direction predicted hardening depth of 1.6 mm, the 2nd direction predicted hardening depth of 2.8 mm, and the 3rd direction predicted hardening depth of 2.7 mm. The error rate of the heating temperature results was 12.2% whereas that of the hardening depth results was 7.1%.
Keywords:
High-frequency heat treatment, Park gear, Resonance RLC circuit, Electromagnetic analysis, Heat transfer analysis, Metal phase transformation키워드:
고주파 열처리, 주차기어, 공진 RLC 회로, 전자기장 해석, 열전달 해석, 상변태 해석1. 서론
열처리 산업의 가장 큰 문제인 에너지 문제 해결을 위해 효율 향상, 품질 고도화 및 환경오염물질 발생 최소화, CO2(이산화탄소) 배출 감소 등 열처리 공정의 청정화 기술에 대한 관심이 증가하고 있다. 고주파 열처리는 기존의 가스 및 기름 등을 이용한 기존 열처리 방식과 다르게 전기를 이용하여 열에너지를 만들기 때문에 친환경적이고 경제적인 장점을 가지고 있다. 이러한 장점으로 인해 국부 경화 열처리 기술로 많이 사용되고 있다.
고주파 열처리는 코일의 형상, 가열물의 형상 및 재질, 주파수의 세기, 입력 전력, 가열시간 및 냉각시간 등 여러 가지 변수에 의해서 품질이 결정된다. 현재 이러한 변수는 숙련된 작업자의 경험에 의존하여 결정하고 실행착오를 거쳐서 제품을 생산한다. 이러한 불필요한 손실을 줄이기 위하여 유한요소해석을 적용한 연구가 1970년대 이래 다양하게 진행되어 왔다. Han et al. [1]은 용접 된 파이프에 860-1,150 Hz의 주파수로 유도가열 시뮬레이션으로 공정변수를 최적화하였고 Li et al. [2]은 고주파 열처리 중 시뮬레이션을 사용하여 볼스크류의 공정변수를 최적화하였다. Lee et al. [3]은 AISI 4140 환봉을 고주파 유도가열 후 온도측정 실험 결과와 유한요소해석 결과를 비교하였으며, Oh et al. [4]은 유한요소해석을 통하여 유도가열 코일의 반경, 간격 등의 설계인자에 따라 온도분포를 계산하였다. Ji et al. [5]은 고주파 유도가열을 이용한 기어 제조를 위한 압연공정을 설계하기 위해 유한요소해석을 사용하였다. 또한 Tak et al. [6]은 유도가열로 대상물을 가열하여 성형성을 향상시키는 연구를 하였다. Tong et al. [7]은 JIS-SCM440의 원통형 부품에 대하여 전자기장-열전달 해석으로 가열 온도 및 냉각 온도를 계산하고 온도에 따른 상변태를 고려한 유한요소해석을 수행하였다. Choi et al. [8-10]은 스프라켓을 고주파 열처리 후 유한요소해석결과와 경화 깊이를 실험으로 측정하여 결과를 비교하였으며, AISI 1045 환봉의 고주파 열처리 과정 중 입력전류를 유한요소해석에 입력하고 가열, 냉각해석으로 얻은 온도와 상변태 결과와 실험 결과로 얻은 경화영역을 비교하였다.
다양한 변수와 관련된 많은 선행 연구들이 존재하지만, 자기장 세기와 연관된 코일 전류에 대한 연구는 전무한 실정이다. 따라서 본 논문에서는 코일 전류 및 상변태를 고려한 고주파 열처리 시뮬레이션 방법을 제안하고자 한다. 이는 공진 RLC 회로를 사용하여 구한 코일 전류와 전자기-열전달-상변태를 적용한 고주파 열처리 시뮬레이션을 다음과 같이 검증하였다.
2. 주차기어의 고주파 열처리
주차기어는 자동차의 트랜스미션에서 동력 전달을 못하도록 잠금 역할을 담당하고 있다. 이 기어의 표면은 높은 피로수명과 내마모성을 가져야 하기에 고주파 열처리로 표면을 경화한다.
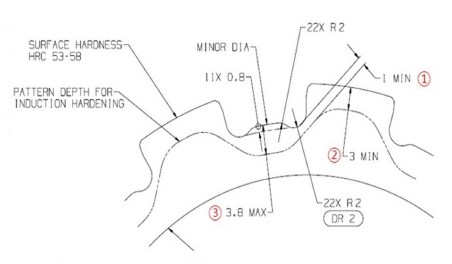
주차기어의 고주파 열처리 실험에 사용된 장비는 Table 1에 정리하였다. 고주파 열처리 시 실험 조건은 20 kHz 주파수, DC203 V 입력전압, DC 409 A 입력전류로 총 83 kW의 입력전력으로 4.5초간 가열 후 8초간 냉각수를 분무하여 냉각시킨다. 고주파 열처리 후 요구되는 경화 깊이는 Fig. 1과 같으며 1번 방향의 요구 경화 깊이는 1 mm, 2번 방향은 3 mm, 3번 방향은 3.8 mm이다. 고주파 열처리는 탄소강을 A1 변태점 온도 이상으로 가열 후 Ms (Martensite Transformation Start) 이하로 급랭하는 과정이다. 탄소 함유량 0.5-0.55%의 AISI 1552의 A1 변태점 온도는 727oC이며 Ms 온도는 223oC이다[11]. 주차기어의 고주파열처리 시 최대 가열 온도는 적외선온도계를 사용하여 5회 측정을 하였으며 측정결과는 Fig. 2와 같으며 평균 가열온도는 977.4oC이다. 최대 가열 온도 측정 결과 A1 변태점 온도 이상 가열된 것을 확인할 수 있다. 고주파 열처리가 된 주차기어를 3%의 나이탈 부식액을 사용하여 에칭(Etching)하여 경화 패턴을 확인 후 경화 깊이를 측정하였다. HV 450을 기준[12]으로 1, 2, 3의 방향으로 마이크로 비커스 경도계로 경화 깊이를 측정하였다. 측정 시 300 g의 하중으로 12초동안 압자를 누르고 시편표면에 생긴 압흔의 표면적을 계산하여 경도를 산출한다. 산출된 경도를 Table 2에 나타내었다. 측정결과 1번 방향의 경화 깊이는 1.5 mm, 2번 방향의 경화 깊이는 3 mm, 3번 방향의 경화 깊이는 2.5 mm임을 확인하였다.
3. 고주파 열처리 시 코일 전류 계산
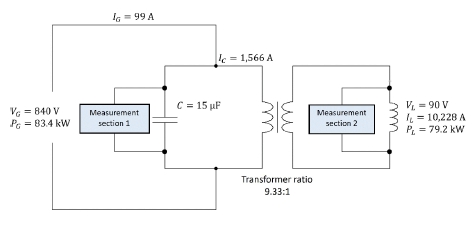
주차기어의 고주파 열처리 시뮬레이션을 위하여 가열 시 코일에 흐르는 전류 값을 알아야 한다. 고주파의 높은 전류는 직접 측정할 수 없기에 전압을 측정하여 공진 RLC 회로에 적용하여 계산한다. Fig. 3(a)와 같이 고주파 유도가열 시스템의 공진탱크(Resonance Tank)의 커패시터(측정부위 1)와 Fig. 3(b)의 코일 (측정부위 2)에서 전압 및 주파수를 오실로스코프를 사용하여 측정하였다. 측정부위 1에서의 전압 및 주파수는 Table 3에서 표시한 것과 같이 AC 840 V, 19.77 kHz이다. 측정부위 2에서의 전압 및 주파수는 AC 90 V, 19.82 kHz의 측정결과를 얻었다. 코일에 흐르는 전류를 계산하기 위해 고주파 유도가열 시스템의 공진탱크를 병렬 공진 RLC 회로에 적용하였다. 입력전압, 전류, 전력, 주파수와 커패시터 용량 15 μF을 적용하여 병렬 공진RLC 회로를 계산[13]하기 위해서는 저항, 인덕턴스를 알아야 한다. 식(1)을 통하여 인덕턴스 L을 구한 뒤 공진탱크의 전체저항 전류를 식(2)와 같이 계산한다. 옴(Ohm)의 법칙을 사용하여 식(3)과 같이 저항을 계산한다. 커패시터에 흐르는 전류를 계산하기 위하여 식(4)와 같이 품질계수(Q-factor) 또는 식(5)와 같이 커페시터 리액턴스를 먼저 구한다. 식(6)을 통하여 커패시터의 전류를 계산할 수 있다. 변압기의 전송비는 식(7)과 같이 커패시터의 전압과 코일에서의 전압을 사용하여 계산한다. 고주파 유도가열 시스템의 전송 효율은 75%이고 변압기 및 리드 손실은 5%이므로 총 효율은 70%이다[11]. 식(8)과 같이 코일에 흐르는 전류는 10,228 A를 계산하였고 Fig. 4에 고주파 유도가열 시스템의 공진탱크의 병렬 공진 RLC 회로에 계산한 결과를 표시하였다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |

Measurement results for the alternating current voltage and frequency in measurement sections 1 and 2
4. 주가기어의 고주파 열처리 시뮬레이션
4.1 전자기장 수학적 모델
고주파 열처리 시뮬레이션을 수행하기 위해서는 먼저 전자기수학적 모델이 필요하다. 전자기장의 계산은 일반적으로 맥스웰방정식을 기본으로 한다. 전자기 특성의 고유 방정식은 다음 식(13)부터 식(15)와 같이 나타낼 수 있으며, 여기서 B는 자속밀도이고 H는 자기장 강도이다. D 및 E는 전속 밀도 및 전자기장강도를 나타내고 J는 전류 밀도를 나타낸다. 보고된 연구에서 교류전류 주파수는 1 MHz 미만일 때 변위전류 ∂D/∂t는 준 정적 근사를 이용한 전도 전류밀도에 비해 무시될 수 있다[14]. ε, μ 및 σ는 유전율, 투자율 및 전기전도도이며 온도에 따라 비선형적으로 변하는 특성이 있다.
| (9) |
| (10) |
| (11) |
전자기장 계산에서 가열된 부분의 와전류 영역과 비와전류영역으로 구성된다. 변수의 양을 줄이고 맥스웰 방정식을 단순화하기 위해 Sadeghipour et al. [15]에 의해 제안된 자기 벡터전위 A와 전기 스칼라 전위 j를 도입 후 쿨롱 게이지(Coulomb Gauge) [16]를 적용한 시간 조화 조건의 와전류 영역 지배 방정식은 식(12), 식(13)과 같이 나타낸다.
| (12) |
| (13) |
4.2 열전달 수학적 모델
전자기장 계산에서 계산된 열에너지 전달에는 푸리에 편미분방정식이 사용되며 식(14)와 같이 표시한다. λ는 열전도도, ρ밀도, c는 비열, Q는 와전류 열을 포함한 내부 열원이다. 가열 대상물 및 주변과 대상물 표면 사이의 열전달은 식(15)와 같이 설명할 수 있다. 여기서 ∂T/∂n은 표면의 온도구배, Tc는 주위온도, h는 식(16), 식(17)과 같이 대류계수 hk 및 열 복사 hs를 포함한 총 열전달 계수이다. σ0는 스테판-볼츠만(Stefan-Boltzmann) 상수이며, εr는 방사율, F*는 열복사의 각각 인자이다.
| (14) |
| (15) |
| (16) |
| (17) |
4.3 상변태 수학적 모델
오스테나이트화 같은 확산 변태에는 미분 공식이 일반적으로 사용된다. 유도가열 시 탄소강의 오스테나이트화는 리브론드-드보(Leblond-Deaux) 모델[17-22]을 사용한다. 온도에 따라 새로운 상변태 및 성장은 식(18)과 같이 나타낸다. 여기서 P는 상분율, t는 시간, T는 온도, 는 평형상태의 상분율을 나타내고 TR은 시간 지연과 온도의 함수로 사용된다. 상변태는 금속 내부에서 발생하고 각각의 발생률은 다른 상변태에 의존한다. 온도와 냉각속도의 함수 TR을 식(19)와 같이 표현이 가능하고 냉각 속도에 따른 상변태에 대한 변수 F, F’를 도입하고 F = F'라고 가정하면 식(20)과 같이 상의 변태율을 계산한다.
| (18) |
| (19) |
| (20) |
마르텐사이트 상변태의 경우 냉각되는 시점의 온도에 의존적으로 반응하며, 코이스티넨-마르부르크(Koistinen-Marburger)의 모델에 기초하여 식(21)과 같이 계산한다[24-27]. 여기서 Pm은 냉각에 의한 상변태 가능 분율이며, Ms와 b는 상변태 시작온도와 변태율을 나타낸다.
| (21) |
4.4 고주파 열처리 시뮬레이션
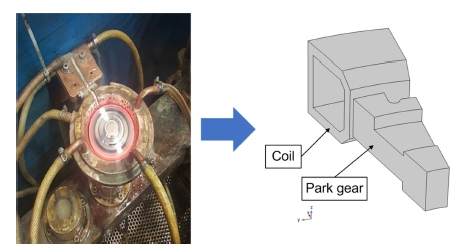
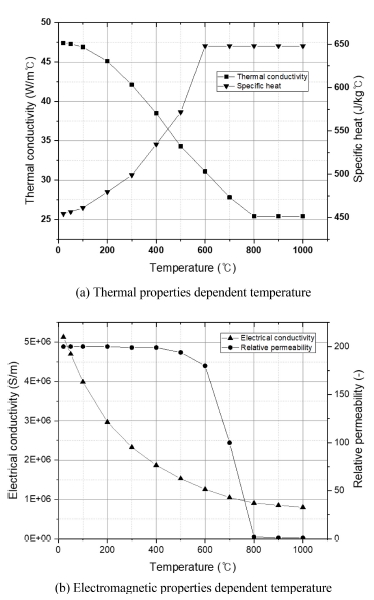
병렬 공진 RLC 회로로 계산된 전류를 검증하기 위하여 Fig. 5와 같이 1/11 축대칭 형상으로 주차기어와 코일을 모델링하였다. 상용 유한요소 해석 프로그램인 COMSOL Multiphysics로 209,471개의 전자기-열전달-상변태 사면체 요소를 사용하였고 시뮬레이션 프로세스는 Fig. 6에 나타냈다. 자기장에 의해 생성되는 와전류는 유도 가열 중에 생성된다. 와전류에 의해 줄열이 발생하여 온도가 상승하게 되며 온도가 A1 변태점 이상으로 가열되면 탄소강의 경우 상변태가 발생하여 페라이트에서 오스테나이트 조직으로 상변태되고 냉각 과정에서 온도가 A1 변태점에서 Ms 온도로 급격히 냉각되면 오스테나이트에서 마르텐사이트로 다시 상변태한다. 온도에 따른 탄소 함유량 0.5-0.55% AISI 1552의 열 및 전자기 특성 곡선[14]을 보여주며 Fig. 7(a)는 온도에 따른 열전도율 및 비열, Fig. 7(b)는 온도에 따른 상대 투자율 및 전기전도도를 나타낸다. AISI 1552 탄소강이 강자성체에서 상자성체로 변하는 전이온도인 퀴리 온도는 약 770oC이다[4]. Fig. 7(b)에서 유도가열 중에 온도가 퀴리 온도를 초과하면 강자성 특성이 손실되며 상변태로 인한 투자율 변화의 영향은 무시할 수 있다[14]. 고주파 열처리 중 상변태는 온도에 따라 달라지게 되며 오스테나이트에서 페라이트, 펄라이트 및 베이나이트 상변태는 리브론드-드보 모델을 사용한다. 페라이트에서 오스테나이트 상변태를 설명하는 온도 종속 함수는 Table 4에 나타냈다. 페라이트에서 형성되는 오스테나이트 분율의 시간 변태율은 식(22)와 같고 오스테나이트 상태에서 냉각되면 여러 상의 형태로 될 수 있다. Table 5는 오스테나이트-베이나이트 온도의 함수를 나타내고, Table 6은 오스테나이트-베이나이트 온도속도의 함수를 나타낸다. 오스테나이트에서 형성된 베이나이트 분획 시간 변태율은 식(23)과 같다[22]. 오스테나이트의 확산 상변태와 달리 마르텐사이트의 상변태는 분포하며, 형성된 마르텐 사이트의 비율은 코이스티넨-마르부르크 모델에 의해 주어진 Ms 온도 이하로의 과냉각에 비례한다. 마르텐사이트 변태율은 식(24)와 같으며 Table 7에 나타냈다[23].
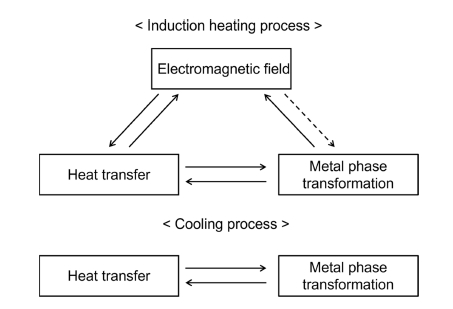
High-frequency heat treatment simulation process: The dashed line does not couple during the simulation
| (22) |
| (23) |
| (24) |
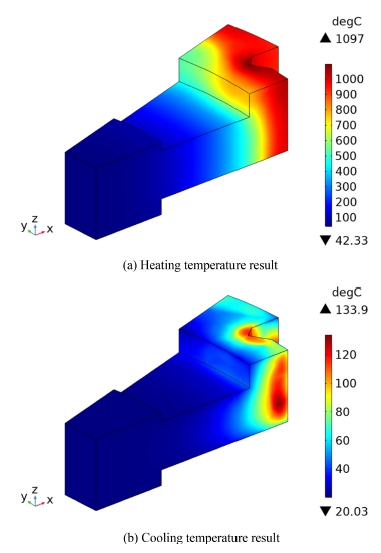
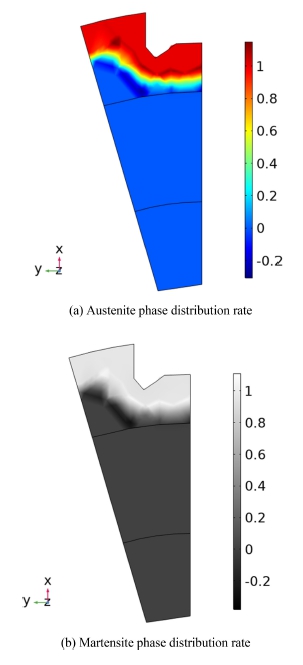
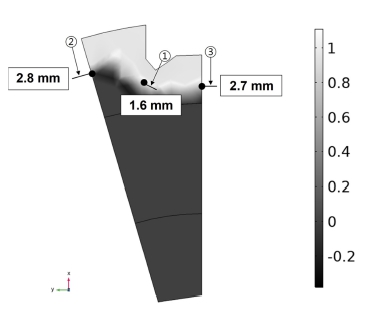
주차기어를 20 kHz에서 10,228 A의 고주파 전류로 4.5초 동안 가열했을 때 가열 중 도달한 최대 온도는 Fig. 8(a)와 같이 1,097oC이며 가열 후 8초 간 에델바우어(Edelbauer) 등[28]의 물 분무 열 전달 계수를 참조하여 냉각 결과는 Fig. 8(b)와 같이 최대 온도 133.9oC이다. 탄소 함유량 0.5-0.55%의 AISI 1552의 A1 변태점 온도인 727oC 이상 가열되어 페이라트에서 오스테나이트로 상변태가 시작됨을 확인할 수 있다. 가열 후 냉각되는 동안 오스테나이트 상이 Ms 온도 223oC 이하로 냉각되어 마르텐사이트로 상변태될 것을 예측할 수 있다. Fig. 9(a)는 4.5초 동안 가열 했을 때 주차기어의 상변태 분포를 나태낸다. A1 변태점 온도 이상 가열되었기에 페라이트에서 오스테나이트로 상변태 된 것을 확인할 수 있다. Fig. 9(b)는 가열 후 8초간 냉각 후 주차기어의 상변태 분포를 나타낸다. 물 분무로 인해 급격히 Ms 온도 이하로 냉각되어 오스테나이트에서 마르텐사이트로 상변태가 된 것을 확인할 수 있다. 주차기어의 경화 깊이를 예측하기 위하여 Fig. 10과 같이 마르텐사이트 분포도에서 예측 경화 깊이를 측정하였으며 1번 방향의 예측 경화 깊이는 1.6 mm, 2번 방향의 예측 경화 깊이는 2.8 mm, 3번 방향의 예측 경화 깊이는 2.7 mm으로 예측했다.
5. 주차기어 고주파 열처리 결과 비교 검증
주차기어의 고주파 열처리 온도 측정 실험과 시뮬레이션 결과를 비교 검증하였다. Fig. 2와 같이 고주파 열처리 시 측정된 평균 온도는 977.4oC였으며, 시뮬레이션 된 최대 가열온도는 Fig. 8(a)와 같이 1,097oC로 11%의 오차가 발생하였다. 그리고 Table 2과 Fig 10의 경화 깊이 측정 결과와 시뮬레이션에 의한 예측 경화 깊이를 비교 결과 1번 방향의 경화 깊이는 1.5 mm, 예측 경화 깊이는 1.6 mm로 오차 6.3%이다. 2번 방향의 경화깊이는 3 mm, 예측 경화 깊이는 2.8 mm로 오차 6.7%이다. 3번 방향의 경화 깊이는 2.5 mm, 예측 경화 깊이는 2.7 mm로 오차 7.4%의 결과를 도출했다. 실험과 시뮬레이션 비교 결과 1, 2, 3번 방향 경화 깊이 오차가 10% 미만인 결과를 통하여 병렬 공진 RLC 회로로 유도가열 시 코일에 흐르는 전류를 올바르게 계산 후 시뮬레이션 되었다는 것을 검증했다.
6. 결론
병렬 공진 RLC 회로와 전자기-열전달-상변태를 이용한 고주파 열처리 시뮬레이션을 AISI 1552 주차기어에 적용했다. 고주파 열처리 시 공진 탱크의 커패시터 용량, 커패시터의 전압, 코일 전압, 주파수, 가열시간, 냉각시간, 가열 온도 및 경화 깊이를 분석하였다. 측정된 커패시터 용량, 커패시터 및 코일의 전압, 주파수를 병렬 공진 RLC 회로를 이용하여 최종적으로 코일에 흐르는 전류를 계산하였다. 온도에 따른 전기적, 열전달 물성치 및 온도에 따른 상변태 함수 및 냉각계수를 적용하여 고주파 열처리 시뮬레이션을 수행하였다. 시뮬레이션의 가열 온도, 냉각 온도, 상변태 분포를 분석하여 예상 경화 깊이를 도출하였다. 시뮬레이션 결과 가열 온도는 87.8%의 정확도, 경화 깊이는 92.9%의 정확도로 산출하였다. 주차기어의 고주파 열처리 연구결과를 통하여 정립된 고주파 유도가열 및 고주파 열처리 시뮬레이션의 신뢰성을 확인하였다.
1) 고주파 유도가열 장치의 저항, 커패시터 용량, 인덕터의 값에 따라 가열 대상물에 침투 전류 깊이와 전류세기가 변하는 특성을 이용하여 공진 RLC 회로에 적용하여 코일 전류 계산이 가능하다.
2) AISI 1552 고주파 유도가열 시 상온에서 650oC까지 도달하는데 2초, 650oC에서 최종 가열 온도까지 도달하는데 2.5초로 가열 효율이 낮아지는 현상이 발생한다. 이는 중탄소강이 600-650oC일 때 자성체에서 비자성체로 변하는 과정에서 투자율이 급격히 낮아지기 때문이다(Fig. 7(b) 참조).
3) 오스테나이트 조직에서 마르텐사이트 조직으로 상변태가 발생하기 위해서는 Ms 온도까지 10초 이내에 냉각되어야 한다. 이를 위하여 물 분사 냉각계수뿐만 아니라 상황에 맞는 냉각계수가 필요하다.
4) 고주파 열처리는 탄소강의 조직을 마르텐사이트 조직으로 상변태 시켜 표면경도와 내피로성, 내마모성을 향상시키는 열처리이다. 이를 시뮬레이션하기 위해서는 온도에 따라 페라이스에서 오스테나이트, 오스테나이트에서 베이나이트 또는 마르텐사이트 상변태를 계산할 수 있는 함수가 필요하다.
본 논문에서 제안된 코일 전류 및 AISI 1552 상변태를 고려한 고주파 열처리 시뮬레이션을 적용하여 다양한 제품의 데이터베이스 구축을 통하여 작업자의 경험과 시행착오로 인한 고주파 열처리 공정을 대체하고, 최적의 작업조건 도출 및 기술개발에 기여할 수 있을 것이라 기대한다.
Acknowledgments
이 논문은 2022년도 교육부의 재원으로 한국연구재단 기초연구사업의 지원을 받아 수행된 연구임(No.2020R1F1A1065983).
REFERENCES
-
Han, Y., Yu, E., Zhang, H., Huang, D., (2013), Numerical analysis on the medium-frequency induction heat treatment of welded pipe, Applied Thermal Engineering, 51(1-2), 212-217.
[https://doi.org/10.1016/j.applthermaleng.2012.08.032]

-
Li, H., He, L., Gai, K., Jiang, R., Zhang, C., Li, M., (2015), Numerical simulation and experimental investigation on the induction hardening of a ball screw, Materials & Design, 87, 863-876.
[https://doi.org/10.1016/j.matdes.2015.08.094]

- Lee, I., Tak, S., Pack, I., Lee, S., (2017), Comparative study on numerical analysis using co-simulation and experimental results for high frequency induction heating on SCM440 round bar, Journal of Aerospace System Engineering, 11(3), 1-7.
-
Oh, D.-W., Kim, T. H., Do, K. H., Park, J. M., Lee, J., (2013), Design and sensitivity analysis of design factors for induction heating system, Journal of the Korean Society for Heat Treatment, 26(5), 233-240.
[https://doi.org/10.12656/jksht.2013.26.5.233]

-
Ji, H., Wang, B., Fu, X., (2017), Study on the induction heating of the workpiece before gear rolling process, AIP Conference Proceedings, 1896(1), 567120010.
[https://doi.org/10.1063/1.5008148]

-
Tak, S.-M., Kang, H.-B., Baek, I.-S., Lee, S.-S., (2019), Improved workability using preheating in the electromagnetic forming process, Journal of Mechanical Science and Technology, 33(6), 2809-2815.
[https://doi.org/10.1007/s12206-019-0527-3]

-
Tong, D., Gu, J., Totten, G. E., (2017), Numerical simulation of induction hardening of a cylindrical part based on multi-physics coupling, Modelling and Simulation in Materials Science and Engineering, 25(3), 035009.
[https://doi.org/10.1088/1361-651X/aa5f7c]

-
Choi, J.-K., Park, K.-S., Lee, S.-S., (2018), Predicting the hardening depth of a sprocket by finite element analysis and its experimental validation for an induction hardening process, Journal of Mechanical Science and Technology, 32(3), 1235-1241.
[https://doi.org/10.1007/s12206-018-0227-4]

-
Choi, J.-K., Park, K.-S., Lee, S.-S., (2018), Prediction of high-frequency induction hardening depth of an AISI 1045 specimen by finite element analysis and experiments, International Journal of Precision Engineering and Manufacturing, 19(12), 1821-1827.
[https://doi.org/10.1007/s12541-018-0210-0]

-
Choi, J., Lee, S., (2020), High-frequency heat treatment of AISI 1045 specimens and current calculations of the induction heating coil using metal phase transformation simulations, Metals, 10(11), 1484.
[https://doi.org/10.3390/met10111484]

-
Rudnev, V., Loveless, D., Cook, R. L., (2017). Handbook of induction heating, Routledge.
[https://doi.org/10.1201/9781315117485]

- KS D 0027, (2002), Methods of measuring case depth for steel hardened by flame or induction hardening process. https://standard.go.kr/KSCI/standardIntro/getStandardSearchView.do
- Electronics Tutorials, Parallel resonance circuit. https://www.electronics-tutorials.ws/accircuits/parallel-resonance.html/
-
Di Luozzo, N., Fontana, M., Arcondo, B., (2012), Modelling of induction heating of carbon steel tubes: Mathematical analysis, numerical simulation and validation, Journal of Alloys and Compounds, 536, S564-S568.
[https://doi.org/10.1016/j.jallcom.2011.12.084]

-
Sadeghipour, K., Dopkin, J., Li, K., (1996), A computer aided finite element/experimental analysis of induction heating process of steel, Computers in Industry, 28(3), 195-205.
[https://doi.org/10.1016/0166-3615(95)00072-0]

-
Power, E. A., Zienau, S., (1959), Coulomb gauge in non-relativistic quantum electro-dynamics and the shape of spectral lines, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 251(999), 427-454.
[https://doi.org/10.1098/rsta.1959.0008]

-
Mondelin, A., Rech, J., Feulvarch, E., Coret, M., (2014), Characterisation of surface martensite-austenite transformation during finish turning of an AISI S15500 stainless steel, International Journal of Machining and Machinability of Materials 7, 15(1-2), 101-121.
[https://doi.org/10.1504/IJMMM.2014.059190]

-
Leblond, J.-B., Devaux, J., Devaux, J., (1989), Mathematical modelling of transformation plasticity in steels I: Case of ideal-plastic phases, International Journal of Plasticity, 5(6), 551-572.
[https://doi.org/10.1016/0749-6419(89)90001-6]

-
Leblond, J.-B., (1989), Mathematical modelling of transformation plasticity in steels II: coupling with strain hardening phenomena, International Journal of Plasticity, 5(6), 573-591.
[https://doi.org/10.1016/0749-6419(89)90002-8]

-
Leblond, J.-B., Mottet, G., Devaux, J., (1986), A theoretical and numerical approach to the plastic behaviour of steels during phase transformations-I. Derivation of general relations, Journal of the Mechanics and Physics of Solids, 34(4), 395-409.
[https://doi.org/10.1016/0022-5096(86)90009-8]

-
Leblond, J.-B., Mottet, G., Devaux, J., (1986), A theoretical and numerical approach to the plastic behaviour of steels during phase transformations-II. Study of classical plasticity for ideal-plastic phases, Journal of the Mechanics and Physics of Solids, 34(4), 411-432.
[https://doi.org/10.1016/0022-5096(86)90010-4]

-
Leblond, J., Devaux, J., (1984), A new kinetic model for anisothermal metallurgical transformations in steels including effect of austenite grain size, Acta Metallurgica, 32(1), 137-146.
[https://doi.org/10.1016/0001-6160(84)90211-6]

-
Koistinen, D. P., Marburger, R. E., (1959), A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels, Acta Metallurgica, 7(1), 59-60.
[https://doi.org/10.1016/0001-6160(59)90170-1]

-
Phadke, S., Pauskar, P., Shivpuri, R., (2004), Computational modeling of phase transformations and mechanical properties during the cooling of hot rolled rod, Journal of Materials Processing Technology, 150(1-2), 107-115.
[https://doi.org/10.1016/j.jmatprotec.2004.01.027]

-
Reti, T., Fried, Z., Felde, I., (2001), Computer simulation of steel quenching process using a multi-phase transformation model, Computational Materials Science, 22(3-4), 261-278.
[https://doi.org/10.1016/S0927-0256(01)00240-3]

-
Reti, T., Bagyinszki, G., Felde, I., Verö, B., Bell, T., (1999), Prediction of as-quenched hardness after rapid austenitization and cooling of surface hardened steels, Computational Materials Science, 15(1), 101-112.
[https://doi.org/10.1016/S0927-0256(98)00128-1]

-
Umemoto, M., Hiramatsu, A., Moriya, A., Watanabe, T., Nanba, S., Nakajima, N., Anan, G., Higo, Y., (1992), Computer modelling of phase transformation from work-hardened austenite, Iron and Steel Institute of Japan International, 32(3), 306-315.
[https://doi.org/10.2355/isijinternational.32.306]

-
Edelbauer, W., Zhang, D., Kopun, R., Stauder, B., (2016), Numerical and experimental investigation of the spray quenching process with an Euler-Eulerian multi-fluid model, Applied Thermal Engineering, 100(5), 1259-1273.
[https://doi.org/10.1016/j.applthermaleng.2016.02.131]


Ph.D. candidate in the School of Mechanical and Aerospace Engineering, Gyeongsang National University. His research interest is electromagnetic application and structural engineering.
E-mail: jinkyu87@gnu.ac.kr

He is working as a Professor in Mechanical and Aerospace Engineering at Gyeongsang National University. His research area includes finite element analysis and optimal design, electromagnetic application and he is involved in numerous innovative research.
E-mail: leess@gnu.ac.kr