고속 정밀 기동 유도탄의 조립 정렬 오차 측정 방안에 대한 연구

2.1 유도탄 조립 정렬 오차 분류

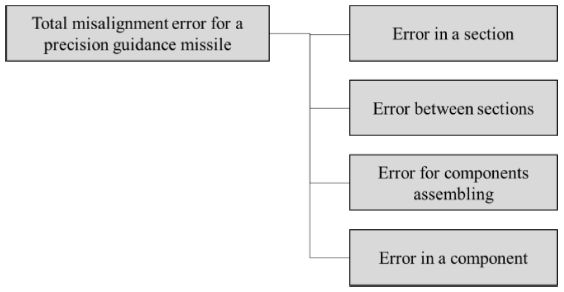
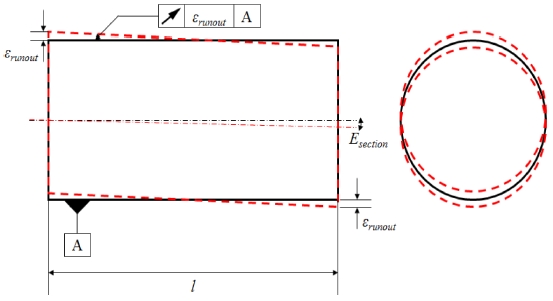
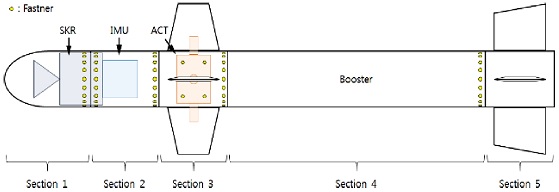
일반적으로 유도탄 조립 시 발생하는 오차는 Fig. 1과 같이 크게 4가지로 분류할 수 있다. 먼저 유도탄을 구성하는 원통형 구조물의 가공 공차에 의해 발생하는 오차를 섹션 내 오차(Error in a Section)로 정의하였다. 이는 원통형 구조물이 이상적인 원통 형상에 비해 얼마나 왜곡되어 있는지를 나타내는 오차로서, 진원도 공차, 진직도 공차, 원통도 공차 및 흔들림 공차 등에 의해 오차 범위가 규제된다. 유도탄 조립체를 측면에서 바라본 2차원 형상으로 단순화 하였을 때, 길이가 l인 섹션이 원통도, 또는 흔들림공차 ε_runout 으로 규제될 경우, 섹션 내 오차에 의한 최대 틀어짐 각도 E_section은 식(1)과 같이 표현할 수 있다.

Fig. 1

Tree structure of the total assembly misalignment error for a precision guidance missile

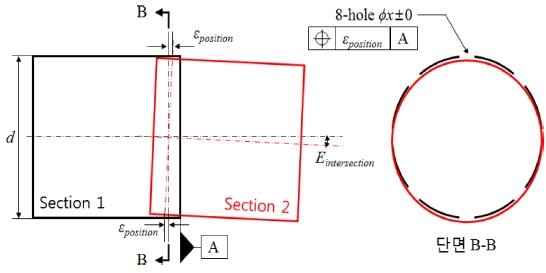
다음으로 유도탄을 구성하는 원통형 구조물 조립 시 발생하는 오차를 섹션 간 오차(Error between Sections)로 정의하였다. 원통 형상의 각 섹션은 Figs. 2와 3과 같이 원주방향으로 배치된 체결홀에 의해서 상호 체결되며, 이 때 각 체결홀은 진위치 공차에 의해 최대 오차 범위가 규제된다. 유도탄 조립체를 측면에서 바라본 2차원 형상으로 단순화 하였을 때, 섹션의 지름이 d이며, 각 체결홀의 진위치 공차가 ε_position으로 규제될 경우, 섹션 간 오차에 의한 최대 틀어짐 각도 E_intersection은 식(2)와 같이 표현할 수 있다.

Fig. 2

Error in a section

Fig. 3

Error between sections

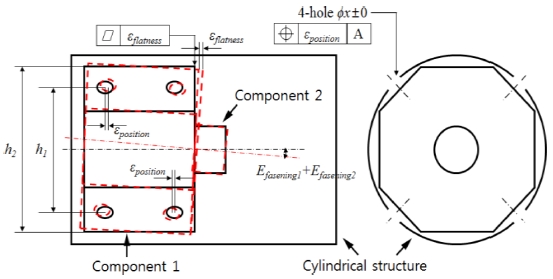
다음으로 유도탄의 주요 구성품이 각 섹션에 체결될 때, 체결 홀의 가공 공차에 따라 발생하는 오차를 구성품 체결 오차(Error for Components Assembling)로 정의하였다. 각 체결 홀은 진위치 공차에 의해 최대 오차 범위가 규제된다. 유도탄 조립체를 측면에서 바라본 2차원 형상으로 단순화 하였을 때, 구성품은 원통 섹션 내경에 직접 조립될 경우와 다른 구성품의 표면에 조립되는 경우의 2가지로 분류할 수 있다.

Fig. 4

Error for components assembling

전자의 경우 구성품을 체결하는 체결홀의 위 아래 거리가 h₁이고, 이 때 각 체결홀이 진위치 공차 ε_position으로 규제될 경우, 구성품 체결 오차에 의한 최대 틀어짐 각도 E_fastening1는 식(3)과 같이 표현될 수 있다. 후자의 경우는 먼저 조립되어있는 구성품의 표면의 평면도 공차를 추가해야 하며, 먼저 조립되어있는 구성품의 위 아래 길이가 h₂이고, 평면도 공차가 ε_flatness 로 규제될 경우 최종 구성품 체결 오차에 의한 틀어짐 각도는 식(4)를 합산해주어야 한다.

마지막으로 체계 조립과 관계 없이 구성품의 가공 또는 조립 시 발생하는 구성품이 내재적으로 가지는 오차를 구성품 오차(Error in a Component)라고 정의하였다. 본 논문에서는 체계 조립에 의한 누적 오차에 대해 분석하기 때문에 구성품 오차에 대해서는 고려하지 않기로 한다.

2.2 유도탄 조립 정렬 오차 정량화 예시

유도탄의 유도 조종 제어를 위해서는 유도탄과 목표물의 상대적인 위치 정보와 유도탄의 자세 정보를 알아야 하며 이를 측정하기 위해 목표물을 탐지 및 추적하는 탐색기(Seeker, SKR)와 자세를 측정하는 관성측정기(IMU)를 탑재한다. 또한 유도탄의 자세를 제어하여 원하는 방향으로 유도탄을 제어하기 위해서는 보편적으로 날개 구동방식을 채택하고 있으며, 구동장치(Actuator, ACT)가 탑재된다. 조종날개를 활용한 공력 제어 방식을 채택한 유도탄에 대하여, 위 세 가지 구성품이 이상적인 위치로부터 벗어나 탑재될 경우 유도 조종 성능 저하가 발생하게 되며, 본 절에서는 이에 대한 정량화를 통해 유도탄의 조립 정렬 오차가 유도탄의 성능 저하에 미치는 영향을 평가하기 위한 정보를 획득하는 예시를 보이고자 한다.

2.1절에서 분류한 각 오차를 정량화 하기 위해, Fig. 5와 같이 5개의 섹션으로 이루어진 유도탄을 가정하였다. 각 섹션은 유도탄의 전방으로부터, 타켓의 위치를 계측하기 위한 탐색기부, 유도탄의 자세를 측정하기 위한 관성항법부, 유도탄을 제어하기 위한 구동부, 유도탄의 추진력을 얻기 위한 추진기관부, 유도탄의 자세를 안정화하고 지상 장치와 연결하기 위한 후방부로 나누어져 있다. 유도탄의 치수는 Table 1과 같이 가정하였다. 계산의 편의를 위해 모든 체결홀의 진위치 공차는 0.3 mm로 가정하였고, 각 섹션은 0.3 mm의 원통도에 의해 규제된다고 가정하였다. IMU는 SKR의 후면판에 장착되는데, 이 때 SKR의 후면판은 0.05 mm의 평면도에 의해 규제된다고 가정하였다. 마지막으로 ACT를 장착하는 위아래 체결홀 간 거리는 260 mm로 가정하였다.

Fig. 5

Missile assembly

Table 1

Comparison of measured roughness data

먼저 유도탄의 자체 자세를 대표하는 IMU의 위치로부터 각 구성품의 상대 틀어짐 각도를 정량화 하였다. 일반적으로 IMU는 SKR의 후면판에 직접 장착되므로 상대적으로 틀어질 수 있는 최대 각도는 SKR 후면판의 평면도에 의해 규제된다. 따라서 유도탄 조립체를 측면에서 바라본 2차원 형상으로 단순화 시켰을 때 IMU와 SKR의 최대 상대 틀어짐 각도는 식(4)에 의해 ±0.009549° 로 계산된다. IMU와 ACT의 상대 틀어짐 각도의 경우, 위 틀어짐 각도에 관성항법부 섹션과 SKR의 체결 오차와, 관성항법부와 구동부의 섹션 간 오차, 관성항법부와 구동부의 각 섹션 내 오차, 그리고 구동부와 ACT의 체결 오차를 합산해 주어야 한다. 그 결과 IMU와 ACT의 최대 상대 틀어짐 각도는 ±0.6574°로 계산된다. 같은 원리로 IMU와 유도탄 기저부의 최대 틀어짐 각도는 ±1.0924°로 계산되며, 이는 지상에 정치되어 기준이 되는 Master IMU와 유도탄에 탑재되어 비행중 운용되는 Slave IMU의 상대 정렬 시 내재될 수 있는 오차와 직접 연관되므로, 성능 저하에 미치는 영향을 세부 검토할 필요성이 예상된다. 또한 여기에서 계산된 틀어짐 각도는 최악의 경우를 단순히 산술적으로 얻어낸 결과인 만큼, 실제 발생하는 틀어짐 각도는 이보다는 낮을 것으로 예상된다.

3.1 경사계 선정 및 측정 치구 설계

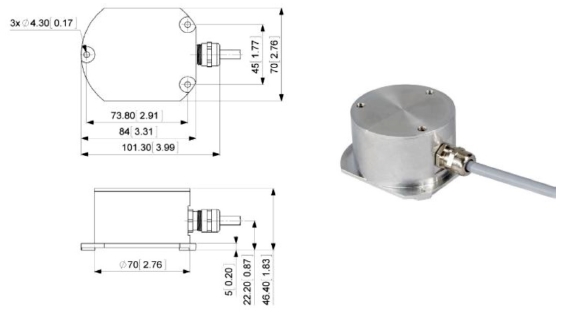
조립 정렬 오차 측정을 위해서는 미세한 위치 틀어짐을 평가할 수 있는 정밀한 장비와 치구가 필요하다. 본 연구에서 측정에 사용한 경사계의 주요 제원은 Table 2⁷와 같으며, 유도탄의 구동부에 요구되는 위치정확도를 고려하여 충분한 정확성과 정밀성을 갖춘 모델을 선정하였다. 선정된 경사계의 형상은 Fig. 6과 같다.

Table 2

Inclinometer general specification

Fig. 6

TILTIX inclinometer (inch.)

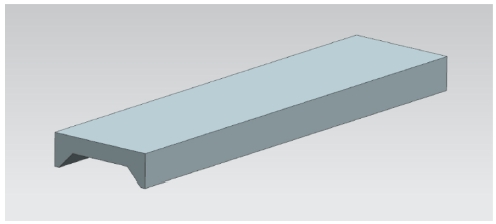
먼저 섹션 내 오차 또는 섹션 간 오차를 측정하기 위해, Fig. 7과 같이 원통형 유도탄 동체 표면과 선 접촉하는 정밀 치구를 설계/제작 하였다. 치구 하단의 움푹 파인 부분이 유도탄의 동체와 맞닿는 부분이며, 상단의 평평한 부분에 경사계를 체결하여 설치한다. 유도탄을 수평 상태로 거치해 둔 상태에서 이 치구를 동체 표면에 거치하여 각도를 측정함으로써, 유도탄의 각 섹션이 수평으로부터 틀어진 각도를 알 수 있으며, 그 절대값 또는 상대 값 비교를 통해 섹션 내 오차와 섹션 간 오차를 직접 도출해낼 수 있다.

Fig. 7

Tool for error in a section and error between sections measurements

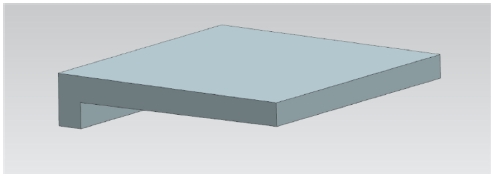
다음으로는 유도탄의 조종날개 체결 오차를 측정하기 위해, Fig. 8과 같이 조종날개 표면과 면 접촉하는 정밀 치구를 설계/제작 하였다. 치구 하단의 경사면과 수직면이 조종날개의 형상과 맞닿도록 설계되어 면 접촉하게 되며, 상단의 평평한 부분에 경사계를 체결하도록 설계하였다. 조종날개 구동각이 0°가 되도록 설정한 뒤, 이 치구를 조종날개 표면에 장착하여 각도를 측정하여 구동부의 섹션 내 오차와 비교함으로써, 조종날개의 체결 오차를 직접 도출해낼 수 있다.

Fig. 8

Tool for control fin assembling error measurements

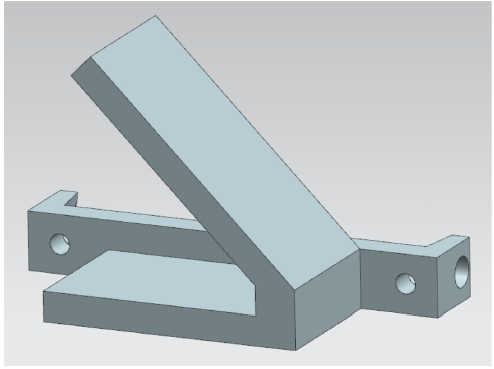
마지막으로 유도탄이 발사관에 장착되는 기저부의 각도를 측정하기 위해, Fig. 9와 같이 기저부에 면 접촉하는 정밀 치구를 설계/제작 하였다. 이 치구는 유도탄의 후방부에 볼트 체결 되며, 필요에 따라 유도탄이 45° 돌아가 있는 상태에서도 경사계를 설치하여 틀어짐 각도를 측정할 수 있도록 경사계 설치 면을 두 개소로 설계하였다. 이 치구를 유도탄의 기저부에 장착하여 각도를 측정함으로써, 유도탄과 발사관이 장착되는 면의 위치를 직접 도출할 수 있으며, 각 섹션 및 구성품의 최종적인 오차가 유도탄의 기저부와 비교하여 얼마나 틀어져 있는지 정량적으로 평가하는 데에 활용할 수 있다.

Fig. 9

Tool for missile base angle measurements

3.2 조종날개 조립 정렬 오차 측정 절차

3.1절에서 선정 및 설계한 경사계와 치구를 활용하여 유도탄의 각 섹션 및 구성품의 조립 정렬 오차를 측정하였다. 2.2절에서 서술한 바와 같이, 공력 제어 방식을 채택한 유도탄에 대하여 성능 분석에 중요한 파라미터가 자세와 조종날개이기 때문에, 본 연구에서는 IMU의 자세 데이터와 각 조종날개의 틀어짐 각도를 측정하여 비교 및 분석하는 데에 초점을 맞추었다.

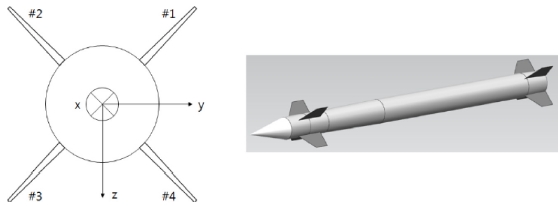
본 연구에서 가정한 유도탄의 경우 4개의 조종날개로 제어되며, 그 배치는 Fig. 10과 같다. 각 날개는 유도탄 축을 중심으로 45°씩 틀어진 상태로 배치가 되어있기 때문에, 각 조종날개의 틀어짐 각도를 측정하기 위해 #1, #3 날개에 대해서는 45°, #2, #4 날개에 대해서는 -45° 유도탄 축을 중심으로 돌려서 고정한 상태로 측정을 수행하였다.

Fig. 10

Configuration of missile and control fins

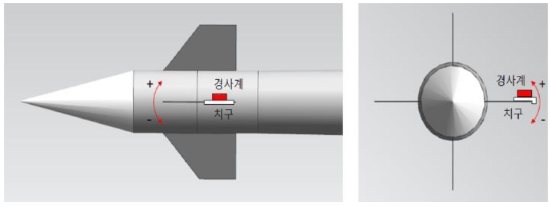
각 날개의 틀어짐 오차는 두가지 형태로 구분하여 측정 및 평가 하였다. 먼저 유도탄을 측면에서 바라보았을 때, 날개가 이상적인 상태보다 틀어지게 조립되어 받음각에 의해 의도치 않은 양력이 발생할 수 있는 오차를 편각(Cant Angle)으로 정의하였다. 편각의 경우 전방을 좌측으로 두고 유도탄을 측면에서 바라보았을 때, 시계 방향으로 회전하는 방향을 +, 반시계 방향으로 회전하는 방향을 –로 정의하였다.

다음으로 유도탄을 후방, 또는 전방에서 바라보았을 때, 날개가 이상적인 상태보다 유도탄의 롤 방향으로 치우쳐진 상태로 탑재된 오차를 전개각(Deployment Angle)으로 정의하였다. 이는 유도탄이 발사관 내에서 접힌 상태로 대기하였다가 발사관 이탈 시 전개되는 운용 방식으로부터 가져온 개념이며, 유도탄을 후방에서 바라보았을 때, 시계 방향으로 회전하는 방향을 +, 반시계 방향으로 회전하는 방향을 –로 정의하였다. 유도탄 조종날개의 편각과 전개각에 대한 개념도를 Fig. 11에 표현하였다.

Fig. 11

Schematic description for cant angle (left) and deployment angle (right) of missile control fins

3.3 IMU 조립 정렬 오차 측정 절차

IMU의 자세 데이터와 각 조종날개의 틀어짐 각도 정량화를 위해, 먼저 유도탄 축을 중심으로 45° 회전시킨 상태로 유도탄을 정치하여 IMU의 조립 정렬 오차를 측정하였다. IMU의 3축 가속도 데이터와 중력가속도를 이용하여, IMU가 조립된 상태에서 조종날개의 편각 방향으로 틀어진 오차와 전개각 방향으로 틀어진 오차는 각각 식(5), 식(6)과 같이 정량화 할 수 있다.

이 때, a_x, a_y, a_z는 3축 가속도계 값이며, 그 방향은 Fig. 10에서 정의한 바와 같다. θ는 IMU의 조종날개 편각 방향 조립 정렬 오차, ϕ는 IMU의 조종날개 전개각 방향 조립 정렬 오차이며, 이 값에는 섹션 내, 섹션 간, 구성품 체결 오차가 모두 포함되어 있다.

4.1 경사계 기반 조립 정렬 측정 방식과 3차원 측정 장비와의 비교 분석

먼저 본 연구에서 제시한 경사계를 활용한 유도탄의 조립 정렬 오차 측정 방식에 대한 검증을 위해, 기존의 3차원 측정 장비를 이용한 측정 방식과 비교 분석을 수행하였다. 검증을 위한 3차원 측정 장비의 주요 제원은 Table 3⁸과 같다. 3차원 측정 장비로 측정한 조종날개의 편각, 전개각과 경사계를 이용한 방법에 대한 비교를 Table 4에 보였다. 두 측정 방법에서 획득한 값의 차이가 0.2° 이내의 값을 보이고 있다. 이 차이는 치구의 제작 정밀도를 개선하거나, 치구 장착 방식을 개선 함으로써 추가적으로 줄여나갈 수 있는 여지가 있으며, Ryu 등⁹이 제시한 바와 같이 일반적인 유도탄 조종날개 구동 점검 장비에 요구되는 정확도와 비교하여 비교할 만한 수준이므로 본 연구에서 제시한 유도탄 조립 정렬 오차 측정 방식에 대한 유효성을 보이는 것으로 판단할 수 있다.

Table 3

3D laser tracker general specification

Table 4

Comparison between TILTIX and LEICA

또한 일반적인 3차원 측정 장비의 경우, 측정 대상물의 크기가 늘어남에 따라 정밀도가 떨어지는 특성을 가지는 경우가 많지만, 본 연구에서 제시된 측정 방안의 경우 대상물의 크기에 정밀도나 정확도가 영향을 받지 않는다는 장점이 있다. 따라서 경사계를 이용한 방식이 기존의 3차원 측정 장비를 이용한 방식과 비교하여 성능 면에서 충분히 정확하고 정밀한 조립 정렬 오차 측정 방식임을 검증할 수 있었다. 측정에 걸리는 시간은 경사계를 이용한 방식과 3차원 측정 장비를 이용한 방식에 큰 차이가 없었다. 하지만 경사계를 이용한 방식이 3차원 측정 장비를 이용한 방식에 비해 비용 절감 효과가 큰 것을 알 수 있었다.

4.2 조종날개와 IMU의 조립 정렬 상대 오차 정량화 예시

다음으로 공력 제어 방식의 유도탄 성능에 직접적인 영향을 주는 조종날개와 IMU의 상대적 조립 정렬 오차를 Fig 12와 같이 측정하여 평가하였으며, 측정 결과를 Table 5에 보였다. 경사계 기반 조립 정렬 오차 측정방식과 기존의 3차원 측정 방식의 차이는 #3 조종날개의 전개각 차이에서 확인할 수 있듯이 최대 약 0.49° 수준으로 검토되었다. 이는 Ryu 등⁹이 제시한 구동장치 점검 장비의 정확도와 비교할만한 수준이며, 경사계 기반 측정 방식과 3차원 측정 방식의 편각과 전개각의 편차 방향(±부호) 또한 일치한다는 점에서 본 연구에서 제시된 방식의 유효성을 확인할 수 있었다.

Fig. 12

Measurement for an assembling error of control fins

Table 5

Comparison between TILTIX and IMU

4.3 유도탄 섹션별 조립 정렬 오차 정량화 예시

다음으로 유도탄의 외형과 탄내 구성품의 조립 오차를 결정하는 섹션별 오차를 Fig. 13과 같이 측정하였다. 주요 섹션의 틀어짐 각도는 발사관에 장착되는 유도탄의 기저부 면과 비교하였으며, 기저부 면의 측정은 Fig. 14와 같이 수행하였다. 섹션별 오차는 유도탄의 Pitch 방향과 Yaw 방향에 대한 틀어짐 각도를 각각 측정하였으며, 결과는 Table 6과 같다. 기존의 3차원 측정장비의 경우, 원통 구조물에 대한 조립 정렬 오차를 확인하기 위해 최소 6 Point 이상의 위치에 대하여 측정 및 계산을 수행해야 했으나, 경사계 기반 조립 정렬 오차 측정 방식의 경우, Figs. 7과 13에 보인 바와 같이 전용 치구를 활용하여 보다 측정 방법이 용이하며, 계측 및 계산에 걸리는 시간도 크게 절약됨을 확인할 수 있었다.

Fig. 13

Measurement for an assembly misalignment of a section

Fig. 14

Measurement for an absolute position of missile base

Table 6

Comparison between TILTIX and IMU

기저부와 각 섹션의 정렬 오차는 유도탄의 비행 시 공기와 맞닿는 면적을 증가시켜 의도치 않은 항력과 양력을 유발시킨다. 각 섹션의 틀어진 각도와 섹션의 길이를 통하여 유도탄의 공력 유효면적 변화량을 계산할 수 있다. 측정 및 계산 결과, 유도탄의 받음각이 0도일 경우, 섹션별 오차로 인하여 발생한 유도탄의 공력 유효면적의 증가는 1.39% 수준이었다. 항력은 일반적으로 속도의 제곱과 비행체의 유효 면적에 각각 비례하므로, 초고속 고기동 유도탄의 경우 정밀 제어에 미치는 영향에 대하여 상세 분석이 필요할 것으로 판단된다.