소형 드론을 위한 주파수 영역 식별과 모델 기반 외란 관측기

1. 서론

드론은 4차 산업 시대의 다양한 기술을 응용할 수 있는 첨단기술 융합산업으로, 조종이 쉽고 비용이 저렴하며 수직 이착륙이 가능하여 교육, 군사, 레저 등 다양한 분야에 활용되고 있다[1].

실내보다 상대적으로 많은 외란이 발생하는 실외에서는 ‘빌딩풍’이나 ‘골짜기 바람’ 같은 돌풍으로 드론이 추락하거나 임무 완료시간이 지연될 수 있다[2]. 특히, 소형 드론은 가볍고 작기 때문에 실외에서 제어 성능이 저하될 수 있어 외란 제거를 위한 기술이 필요하다.

드론의 외란 제거를 위해 인공신경망 등 여러 기법들이 사용되고 있지만 돌풍과 같은 불규칙적인 환경에서는 학습 및 제어의 복잡성 등 한계점이 있다[3]. 모델 기반 외란 관측기(Disturbance Observer, DOB)는 간단한 구조로 유입된 등가 외란을 추정하여 효과적으로 외란을 제거할 수 있다[4].

모델 기반 외란 관측기 적용을 위한 공칭 모델은 시스템 모델링이나 식별로 구할 수 있다. 질량, 관성 모멘트 그리고 공진주파수와 같은 기계 시스템의 동역학 모델 정보를 얻기 위해 시간 영역보다는 주파수 영역 시스템 식별이 유리하다[5].

Matlab과 Simulink는 드론 제어 시스템 개발 및 성능 분석에 많이 사용된다. Matlab과 연동되는 드론 중 Parrot Mambo는 비교적 저렴하며 높은 기동성을 가진다[6].

이 논문에서는 소형 드론 주파수 영역 식별을 수행하고 모델기반 외란 관측기를 적용하여 돌풍에 강건한 드론을 구현하였다. Matlab과 Simulink를 이용하여 다중 정현파 가진에 대한 소형 드론의 주파수 응답을 측정하고 시스템 식별을 수행한다. 식별한 모델 기반으로 외란 관측기를 설계하고 정현파 외란 제거성능을 비교하여 그 유효성을 실험적으로 검증한다. 최종적으로 서큘레이터를 이용해 실제 돌풍 외란을 가하고 외란 관측기 성능을 실험적으로 확인하였다.

2. 시스템 모델링

2.1 드론의 수학 모델

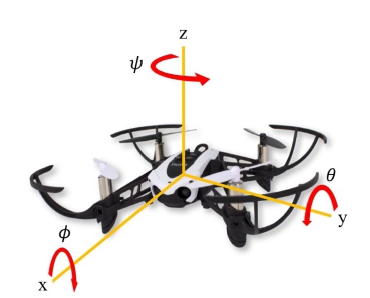
Fig. 1에 드론 좌표계를 나타냈다. S는 sin, C는 cos, x, y, z는 관성 좌표계 내 상대위치, g는 중력 가속도, Φ, θ, Ψ는 오일러 각, I는 관성 모멘트, J_r 은 모터 회전자 관성 모멘트, Ω_d는 모터의 각속도 총합, U_z, U_Φ, U_θ, U_Ψ는 제어 추력 및 토크 입력을 의미한다.

Fig. 1

The coordinate for mathematical model of the drone

뉴턴-오일러 방정식을 기반으로 유도한 드론의 수학적 모델[7]은 식(1), 식(2)와 같다. 식(1)은 병진 운동을 나타내고, 식(2)는 회전 운동을 나타낸다. 드론은 호버링 상태에서 식(3)을 만족한다[8]. 회전하는 모터는 추력과 토크를 생성하며 식(4)가 성립한다[9].

$\[ \left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right]=\frac{1}{m}{U}_z\left[\begin{array}{c}S\psi S\varphi +C\varphi S\theta C\psi \\ -C\psi S\varphi +C\varphi S\theta S\psi \\ C\varphi C\theta \end{array}\right]-\left[\begin{array}{c}0\\ 0\\ g\end{array}\right] \]$

(1)

$\[ \left[\begin{array}{c}\ddot{\varphi }\\ \ddot{\theta }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{c}\frac{\left(I_{yy}-I_{ZZ}\right)}{I_{xx}}\\ \frac{\left(I_{zz}-I_{yy}\right)}{I_{yy}}\\ \frac{\left(I_{xx}-I_{yy}\right)}{I_{ZZ}}\end{array}\right]-J_r\left[\begin{array}{c}\frac{\dot{\theta }}{I_{xx}}\\ -\frac{\dot{\varphi }}{I_{yy}}\\ 0\end{array}\right]{\Omega }_d+\left[\begin{array}{c}\frac{1}{I_{xx}}{U}_{\varphi }\\ \frac{1}{I_{yy}}{U}_{\theta }\\ \frac{1}{I_{zz}}{U}_{\psi }\end{array}\right] \]$

(2)

$\[ \begin{array}{c}\left[U_z,U_{\varphi },U_{\theta },U_{\psi }\right]=\left[\begin{array}{cccc}mg& 0& 0& 0\end{array}\right]\\ \left[\begin{array}{ccc}\ddot{\varphi }& \ddot{\theta }& \ddot{\psi }\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\end{array}\right]\\ \left[\begin{array}{ccc}\dot{\varphi }& \dot{\theta }& \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\end{array}\right]\\ \left[\begin{array}{ccc}\varphi & \theta & \psi \end{array}\right]=\left[\begin{array}{ccc}0& 0& \psi \end{array}\right]\\ \left[\begin{array}{ccc}x& y& z\end{array}\right]=\left[\begin{array}{ccc}x& y& z\end{array}\right]\\ \end{array} \]$

(3)

$\[ \begin{array}{c}{f}_i=b{\omega }_i^2\\ {\tau }_{M_i}=d{\omega }_i^2+J_r{\dot{\omega }}_i\end{array} \]$

(4)

f는 모터 축 방향 추력, τ_M은 모터 토크, b는 추력 계수, d는 항력 계수, ω와 $$ \dot{\omega }$$는 각각 모터 각속도와 각가속도를 의미한다. 보통 $$ {\dot{\omega }}_i$$의 영향은 매우 작기 때문에 $$ J_r{\dot{\omega }}_i$$항은 생략된다.

드론 고도 및 롤, 피치, 요 전달함수는 식(1)부터 식(3)을 통해 식(5)와 같이 표현할 수 있다.

$\[ \begin{array}{c}G{\left(s\right)}_z=\frac{z}{f}=\frac{1}{m{s}^2}\\ G{\left(s\right)}_R=\frac{\varphi }{\tau }=\frac{1}{I_{xx}{s}^2}\\ G{\left(s\right)}_P=\frac{\theta }{\tau }=\frac{1}{I_{yy}{s}^2}\\ G{\left(s\right)}_Y=\frac{\psi }{\tau }=\frac{1}{I_{zz}{s}^2}\end{array} \]$

(5)

2.2 소형 드론 Parrot Mambo

Parrot Mambo는 180 × 180 × 58 mm 크기의 소형 드론이다. 3축 가속도와 3축 자이로를 포함한 6자유도 IMU (Inertial Measurement Unit) 센서, 초음파 센서, 기압 센서, 120 × 160픽셀 해상도 60FPS 카메라가 장착되어 있다. 또한 Matlab과 Simulink 패키지를 지원하여 드론 비행 및 제어 알고리즘을 변경할 수 있으며 블루투스를 이용하여 0.005초마다 센서 정보를 수집할 수 있다[8]. Table 1은 Parrot Mambo 드론의 물리 정보를 나타냈다.

Table 1

Physical parameters of the Parrot Mambo

2.3 제어 시스템 구성

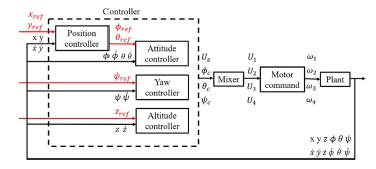
Parrot Mambo 제어시스템에는 Fig. 2와 같이 위치, 자세, 요, 고도 PID 제어기를 사용한다. 각각의 제어기를 통해 기준 입력에 대응하는 제어값인 U_z, Φ_c, θ_c, Ψ_c가 출력된다. U_z는 필요 추력 제어값, Φ_c, θ_c, Ψ_c는 각각 필요 롤, 피치, 요 각도 제어값를 의미한다. 각 모터가 내야 할 추력인 U₁, U₂, U₃, U₄는 단위 제어값 당 추력을 나타내는 Mixer 블록을 통해 식(6)과 같이 계산된다. 이후, Motor Command 블록을 통해 추력 값이 모터 각 속도 명령인 ω₁, ω₂, ω₃, ω₄로 변환된다.

Fig. 2

Control system of the drone

$\[ \left[\begin{array}{c}{U}_1\\ U_2\\ U_3\\ U_4\end{array}\right]=\left[\begin{array}{cccc}0.25& -5.666& -5.666& 103.574\\ 0.25& 5.666& -5.666& -103.574\\ 0.25& 5.666& 5.666& 103.574\\ 0.25& -5.666& 5.666& -103.574\end{array}\right]\left[\begin{array}{c}{U}_z\\ {\varphi }_c\\ {\theta }_c\\ {\psi }_c\end{array}\right] \]$

(6)

3. 주파수 응답

3.1 드론 주파수 응답 측정

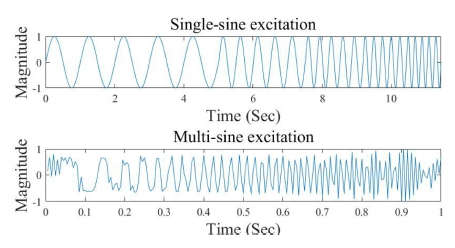
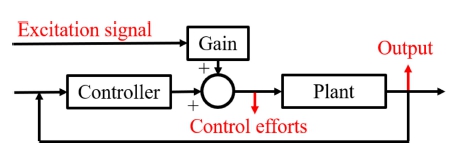
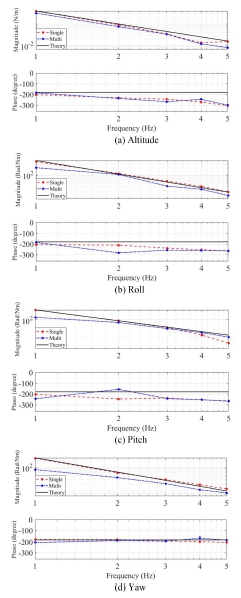
Fig. 3과 같이 1에서 5 Hz까지 1 Hz 간격의 정현파와 다중 정현파로 가진하고 Fig. 4의 Control Efforts와 Output에서 응답을 받아 소형 드론 주파수 응답을 측정하였다. 적절한 응답을 위해 가진 응답이 드론이 호버링 시 발생하는 응답의 3배가 되도록 가진 신호 크기를 결정하였다. Table 2는 각 외란 입력의 이득 값을 정리한 표이다.

Fig. 3

Single-sine and multi-sine excitation signals

Fig. 4

Input and outputs for frequency domain identification

Table 2

Gain of excitation signals

식(6)에서 계산한 U₁, U₂, U₃, U₄는 각 모터가 내야 할 추력이기 때문에 관성모멘트에 대한 보드 선도를 작성하기 위하여 토크 입력으로 변환해야 한다. 식(4), 식(6) 그리고 Table 1을 통해 롤, 피치, 요에 대한 제어값-토크 계수를 구할 수 있다. 요에 대한 1번 모터의 토크를 구하면 식(7)과 같고 모든 모터의 토크 값을 더하면 식(8)과 같다. 또한, 롤에 대한 1번 모터의 토크를 구하면 식(9), 식(10)과 같다. 피치에 대한 제어값-토크 계수도 롤과 같은 방식으로 구할 수 있다.

$\[ {\tau }_{M_{1 ,\psi }}=\frac{d}{b}{U}_{1, \psi }=\frac{0.78264\cdot {10}^{-3}}{0.0107}\cdot 103.5736\cdot {\psi }_c=7.58{\psi }_c \]$

(7)

$\[ \tau ={\tau }_{M_1}+{\tau }_{M_3}-\left({\tau }_{M_2}+{\tau }_{M_4}\right)=30.3{\psi }_c \]$

(8)

$\[ {\tau }_{M_{1, \varphi }}=\frac{l}{2}{U}_{1, \varphi }=\frac{0.624}{2}\cdot \left(-5.6659\right)\cdot {\varphi }_c=-1.77{\varphi }_c \]$

(9)

$\[ \tau =-\left({\tau }_{M_1}+{\tau }_{M_3}\right)+{\tau }_{M_2}+{\tau }_{M_4}=7.07{\varphi }_c \]$

(10)

3.2 주파수 응답 측정 결과

측정한 주파수 응답으로 드론 물리 모델을 식별하였고 Fig. 5에서와 같이 이론 모델과 비교하여 그 신뢰성을 확인하였다. Table 3은 정현파와 다중 정현파로 가진하여 측정한 주파수 응답과 이론적으로 예측한 응답 차이를 나타낸다. 정현파 가진을 통한 시스템 식별이 이론 모델을 더 잘 근사함을 알 수 있다.

Fig. 5

Bode plot of drone

Table 3

Magnitude, phase errors of system identification

4. 외란 관측기

4.1 외란 관측기 설계

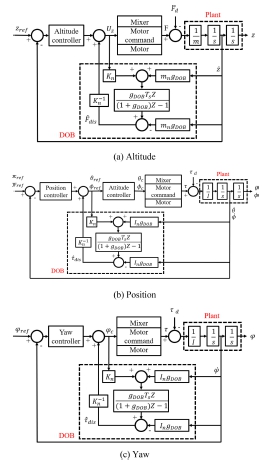
이 논문에서는 고도, 위치, 요 제어기에 외란 관측기를 사용하였으며 사용한 외란 관측기 구조는 Fig. 6과 같다[6]. F_d는 외란, m_n는 공칭 질량, m은 실제 질량, g_DOB는 외란 관측기 대역, K_n은 공칭 추력 계수, K는 실제 추력 계수, $$ {\widehat{F}}_{dis}$$는 외란 추정치를 의미한다. 외란 관측기 기반 제어 시스템은 플랜트에 유입된 외란과 동일한 등가 외란을 추정하여 그 차이를 보상한다. 실험으로 식별한 공칭 질량은 고도 외란 관측기에 사용하고, 공칭롤, 피치 관성 모멘트는 위치 외란 관측기, 공칭 요 관성 모멘트는 요 외란 관측기에 사용하였다. 외란 관측기 대역은 외란 주파수의 10배, 추력 계수는 제어값-토크 계수인 외란 관측기를 설계하였다.

Fig. 6

DOB structure of a drone controller [6] (Adapted from Ref. 6 with website)

4.2 정현파 외란 제거 실험

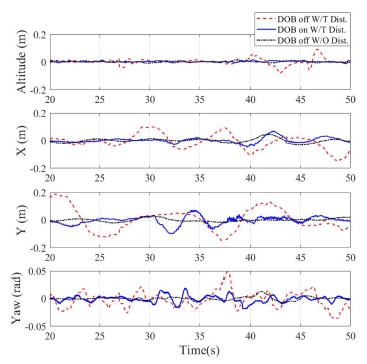
0.5와 1 Hz 정현파 외란을 가하고 외란 관측기 적용 여부에 따른 정현파 외란 제거 성능을 Fig. 7에 나타냈다. Table 4는 외란 관측기 적용 여부에 따른 외란 응답 크기와 외란 응답 감소율을 나타냈다. 모델 기반 DOB를 적용하여 드론 고도 응답의 84.5%, x 응답의 50.7%, y 응답의 52.1%, 요 응답의 79.7%가 제거되었다. 식(1)의 롤, 피치, 요가 결합된 비선형 모델 때문에 고도나 요의 외란 제거 성능이 위치 외란 성능보다 우수하게 나온다.

Fig. 7

Sinusoidal disturbance rejection of the drone W/T and W/O DOB

Table 4

Sinusoidal disturbance removal rate of the drone W/T and W/O DOB

4.3 돌풍 외란 제거 실험

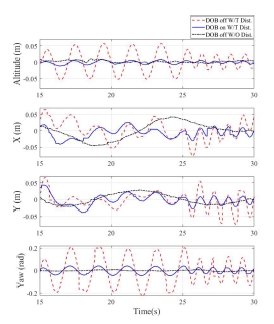
330 × 300 × 403 mm 크기 신일전자 SIF-KC15 서큘레이터로 풍속과 풍향을 변경시키며 외란을 부가하고 외란 관측기가 고도 및 롤, 피치, 요 제어기에 적용된 드론의 비행안정성을 Fig. 8과 같이 실험적으로 확인하였다. 서큘레이터의 풍속은 1.5 m/s, 서큘레이터와 드론 사이 거리는 2 m, 상하 풍향은 0.464 rad로 결정하였고, 좌우 풍향은 1.31 rad 범위에서 0.131 rad/s로 변화시켰다. 확장 칼만 필터(EKF)를 사용하여 드리프트 현상에 따른 IMU 센서의 불확실성을 제거하였으며 Fig. 9와 Table 5에 외란 관측기 적용 여부에 따른 드론의 외란 제거 성능을 나타냈다. 모델 기반 DOB를 적용하여 드론의 고도 변화가 87.7%, x위치 변화가 53.0%, y 위치 변화가 60.6% 그리고 요 각도 변화가 56.2% 감소하였다.

Fig. 8

Disturbance rejection experiments with a circulator

Fig. 9

Disturbance rejection results with a circulator

Table 5

Disturbance removal rate with a circulator

5. 결론

이 논문에서는 소형 드론의 주파수 영역 식별을 수행하고 모델 기반 외란 관측기를 적용하여 돌풍에 강건한 드론을 구현했다. Matlab과 Simulink를 이용하여 다중 정현파 가진에 대한 소형 드론의 주파수 응답을 측정하고 시스템 식별을 수행했다. 모델 기반 DOB를 적용한 후 정현파 외란에 대해 드론 고도 외란 응답의 84.5%, x 외란 응답의 50.7%, y 외란 응답의 52.1%, 요 외란 응답의 79.7%가 제거되었다. 마지막으로 서큘레이터를 이용해 바람의 속도 및 풍향이 변하는 외란을 드론에 가하고 외란 응답 측정 실험을 하였다. 모델 기반 DOB 적용 후 드론의 고도 변화가 87.7%, x 위치 변화가 53.0%, y 위치 변화가 60.6% 그리고 요 각도 변화가 56.2% 감소하였다.

REFERENCES

• Korea Institute of Aviation Safety Technology, Domestic and foreign drone industry trends analysis report. http://www.kdrone.org/bbs/board.php?bo_table=data_rep&wr_id=18&sst=wr_hit&sod=desc&sop=and&page=1
• Aviation and Railway Accident Investigation Board, Aircraft accident report. https://araib.molit.go.kr/USR/airboard0201/m_34497/lst.jsp
• Chen, Z., Liu, C., Su, H., Liang, X., Zheng, M., (2022), A hybrid disturbance observer for delivery drone’s oscillation suppression, Mechatronics, 88, 102907. [https://doi.org/10.1016/j.mechatronics.2022.102907]
• Sariyildiz, E., (2021), A guide to design disturbance observer-based motion control systems in discrete-time domain, Proceedings of the 2021 IEEE International Conference on Mechatronics (ICM), 1-6. [https://doi.org/10.1109/ICM46511.2021.9385674]
• Grauer, J. A., Boucher, M. J., (2020), Aircraft system identification from multisine inputs and frequency responses, Journal of Guidance, Control, and Dynamics, 43(12), 2391-2398. [https://doi.org/10.2514/1.G005131]
• MathWorks, Parrot minidrones support from Simulink. https://kr.mathworks.com/hardware-support/parrot-minidrones.html
• Noordin, A., Basri, M., Mohamed, Z., (2020), Simulation and experimental study on PID control of a quadrotor MAV with perturbation, Bulletin of Electrical Engineering and Informatics, 9(5), 1811-1818. [https://doi.org/10.11591/eei.v9i5.2158]
• Kaplan, M. R., Eraslan, A., Beke, A., Kumbasar, T., (2019), Altitude and position control of parrot mambo minidrone with PID and fuzzy PID controllers, Proceedings of the 2019 International Conference on Electrical and Electronics Engineering (ELECO), 785-789. [https://doi.org/10.23919/ELECO47770.2019.8990445]
• Luukkonen, T., (2011), Modelling and control of quadcopter. https://sal.aalto.fi/publications/pdf-files/eluu11_public.pdf