A Comparative Analysis of AEH (Asymptotic Expansion Homogenization) Results and Experimental Findings of Various Additive Manufactured Lattice Structures

1. Introduction

Lattice structures are concerning in different fields such as biomedical engineering, automotive or aerospace industry, and light weight design as they often exhibit versatile physical properties. Lattice structures provide great strength-to-weight ratio, significant permeability, and outstanding impact-absorption [1,2]. Several lattice cell compositions have been discovered in the past few decades and the most widely studied are the simple-cubic, body-centered cubic (BCC), face-centered cubic (FCC), and their combination such as the simple-cubic body-centered and simple-cubic faced-centered structures, in which their mechanical properties has been investigated [3-8].

To determine the effective mechanical properties of those lattice structures, there are several available methods such as: experimental approaches, analytical modeling, and finite element method [9-20]. However, each of the above approaches has its limitations. For example, the experimental approach is a time-consuming process, budgetary expensive and the results are highly subjective due to the possibility of human error. In the theoretical modeling, assumptions affect the solution, and it is difficult to use for complex problems. In the case of finite element method approach, the computational cost for complex problems is expensive and the results can have some error if the periodic boundary conditions cannot be implemented in the case of unit-cell analysis.

On the other hand, the AEH method is an alternative approach that can handle the time-consuming process, the size effect problem, and the high computational cost inconveniences that the traditional methods possess [21,22]. This advantage comes from the fact that AEH method establishes a relationship between the macroscopic and microscopic field to predict the effective mechanical properties of structures by analyzing the representative volume element (RVE) which is the smallest volume or unit that captures the microstructural features and behaviors of a whole structure or material. More specifically, RVE is a unit volume within a heterogeneous material that is selected to be statistically representative of the entire composite structure [23,24].

AEH method has been successfully applied to a wide range of different configurations and composition of composite materials [25-27] and in contemporary engineering applications including nanotechnologies [28,29], smart composite modeling [30,31], modeling of thin network structures [32] thanks to its effectiveness to predict mechanical properties precisely without high computational cost.

Meanwhile, additive manufacturing (AM) has gained attention for the fabrication of lattice structures after appearance of rapid prototyping. AM is a manufacturing process that involves creating objects layer by layer from 3D model data. This layer-by-layer manufacturing approach is very thankful because it is possible to manufacture complex structures which could not be fabricated by conventional manufacturing process. AM processes are categorized as: binder jetting, direct energy deposition, material extrusion, material jetting, power bed fusion, sheet lamination, and vat photopolymerization [33]. Within the category of vat photopolymerization process, the utilization of stereolithographic (SLA) 3D printing is now becoming more accessible to end users with the appearance of affordable printers on the market. SLA printing technology allows the fabrication of prototypes and final products with the main advantage to fabricate products precisely with high resolution [34].

Therefore, the models in this study were manufactured using an SLA 3D printer and we performed compressive experiments using a universal testing machine (UTM) on the fabricates specimens to validate the result obtained by the numerical model based on AEH method and it was confirmed that this method is an advantageous approach to calculate the effective mechanical properties of lattice structures.

2. Design and Fabrication of Unit-cell

2.1 Design of Unit-cell

The unit-cells were designed using the software SolidWorks2020 (CAD software, Dassault Systèmes SolidWorks Corp., Waltham, MA, USA). The lattice structures analyzed in this study are the SC (Simple Cubic) truss, BCC (Body Centered Cubic) truss, FCC (Face Centered Cubic) truss, SC-BCC (Simple Cubic-Body Centered Cubic) truss, and SC-FCC (Simple Cubic-Face Centered Cubic) truss. For the clear numerical comparison, every characteristic dimension of specimens is set as dimensionless value of 1.0 and the important proportions are depicted in Fig. 1 and Table 1. Furthermore, in order that the porosity has no influence on the effective stiffness of the structures, all the structures were designed to have same porosity of 50%.

Fig. 1

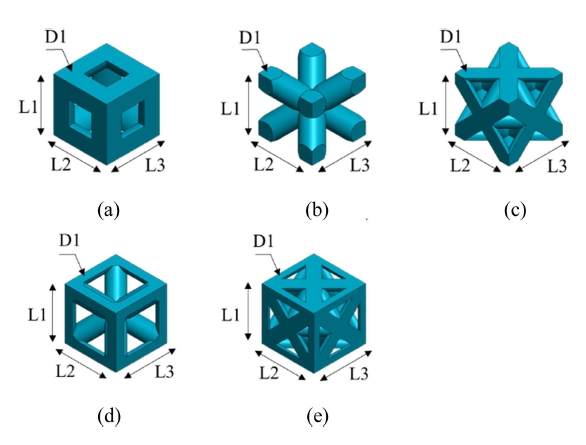
Structural schematics and parameters of unit-cells: (a) SC truss, (b) BCC truss, (c) FCC truss, (d) SC-BCC truss, (e) SC-FCC truss (L: length of strand, D: diameter of strand)

Table 1

Dimensionless value for the parameters of unit-cells

2.3 Prediction of Effective Stiffness by AEH Method

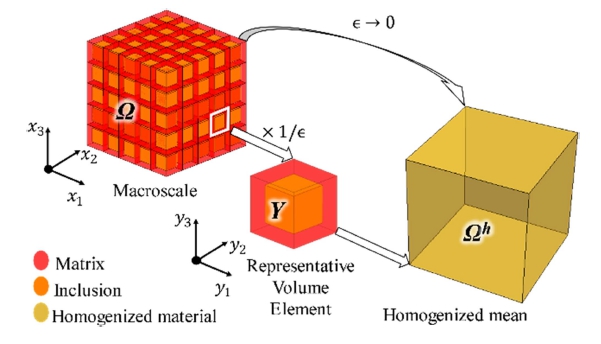
The AEH (Asymptotic Expansion Homogenization method) [21,22] considers that the micro-mechanical behavior of a heterogeneous material can be expressed by considering periodicity within a unit-cell over the entire material as illustrated in Fig. 2. The macroscopy model Ω, which represents the overall structure is described by coordinates x_i. On the other hand, the repetitive unit-cell, which is the microscale model Y, is defined by coordinates y_i.

Fig. 2

Schematic of asymptotic homogenization method

The parameter ε establishes a relationship between the characteristic dimensions of the microscale and macroscale. Since there is a significant difference in size between these two scales, the value of ε needs to be relatively small (ε≪1)

$\[ y=\frac{x}{\epsilon } \]$

(1)

The Y-periodicity of the microstructural heterogeneities refers to the functional dependence on y, which repeats itself periodically within the Y-period. This property is reflected in the elasticity tensor D, where its components are Y-periodic in y. On the other hand, at the macroscale level, the material is considered homogeneous. Thus, the components of the elasticity tensor can be represented as:

$\[ D_{ijkl}=D_{ijkl}\left(y\right) \]$

(2)

Nevertheless, in terms of the macroscale system of coordinates x, the microstructural heterogeneity manifests itself in periods ε^-1 that are less than the characteristic dimension of the domain Y. Following expression (1), the relationship is represented as:

$\[ D_{ijkl}^{\epsilon } \left(x\right)= D_{ijkl}\frac{x}{\epsilon } \]$

(3)

in which D_ijkl denotes the elastic properties corresponding to the microscale model Y. Once the tensor D_ijkl is calculated, we can use it to determine the elasticity tensor $$ D_{ijkl}^{\epsilon }\left(x\right)$$in coordinates x_i for the macroscale model.

Then, the linear-elasticity problem can be mathematical stated as:

$\[ \frac{\partial {\sigma }_{ij}^{\epsilon }}{\partial x_j^{\epsilon }}+f_i=0 in \Omega \]$

(4)

$\[ {\epsilon }_{ij}^{\epsilon }\frac{1}{2}\left(\frac{\partial u_i^{\epsilon }}{\partial x_j^{\epsilon }}+\frac{\partial u_j^{\epsilon }}{\partial x_i^{\epsilon }}\right) in \Omega \]$

(5)

$\[ {\sigma }_{ij}^{\epsilon }=D_{ijkl}^{\epsilon }{\epsilon }_{kl}^{\epsilon } in \Omega \]$

(6)

$\[ u_i^{\epsilon }={\stackrel{-}{u}}_i in {\Gamma }_u \]$

(7)

$\[ {\sigma }_{ij}^{\epsilon }{n}_j={\stackrel{-}{t}}_i in {\Gamma }_t \]$

(8)

the components of the Cauchy stress tensor are denoted by σ_ij while the strain tensor’s components in the macroscale coordinates x_i are denoted by ε_ij. The presence of repeated indices in the preceding equations signifies that we are performing a summation over the three coordinates.

Taking into account the presence of two different scales that characterize the material behavior at the macroscale Ω and microscale Y, the displacement field is approached employing the following asymptotic expansion with respect to the parameter ε:

$\[ u_i^{\epsilon }\left(x\right)=u_i^{\left(0\right)}\left(x,y\right)+\epsilon u_i^{\left(1\right)}\left(x,y\right)+{\epsilon }^2{u}_i^{\left(2\right)}\left(x,y\right)+\dots \]$

(9)

Since we are dealing with two different coordinate systems, x_i and y_i, in the derivation equations, we can consider the following chain rule expansion:

$\[ \frac{\partial }{\partial x_i^{\epsilon }}=\frac{\partial }{\partial x_i}+\frac{1}{\mathrm{\epsilon }}\frac{\partial }{\partial y_i} \]$

(10)

The chain rule of the precedent Eq. (10) can be implemented into Eq. (9), consequently, we determine the components of strain and stress:

$\[ {\epsilon }_{ij}^{\epsilon }={\epsilon }^{-1}{\epsilon }_{ij}^{\left(0\right)}+{\epsilon }^0{\epsilon }_{ij}^{\left(1\right)}+{\epsilon }^1{\epsilon }_{ij}^{\left(2\right)}\cdots \]$

(11)

$\[ {\sigma }_{ij}^{\epsilon }={\epsilon }^{-1}{\sigma }_{ij}^{\left(0\right)}+{\epsilon }^0{\sigma }_{ij}^{\left(1\right)}+{\epsilon }^1{\sigma }_{ij}^{\left(2\right)}\cdots \]$

(12)

Where:

$\[ {\epsilon }_{ij}^{\left(0\right)}=\frac{1}{2}\left(\frac{\partial u_i^{\left(0\right)}}{\partial y_j}+\frac{\partial u_j^{\left(0\right)}}{\partial y_i}\right) \]$

(13)

Then, replacing Eq. (9) within Eq. (5) which is the strain-displacement relationship and implementing the result in Eq. (6), we obtain an equation that relies on ε:

$\[ {\epsilon }^{-2}\frac{\partial {\sigma }_{ij}^{\left(0\right)}}{\partial y_j}+{\epsilon }^{-1}\left(\frac{\partial {\sigma }_{ij}^{\left(0\right)}}{\partial x_j}+\frac{\partial {\sigma }_{ij}^{\left(1\right)}}{\partial y_j}\right)+{\epsilon }^0\left(\frac{\partial {\sigma }_{ij}^{\left(1\right)}}{\partial x_j}+\frac{\partial {\sigma }_{ij}^{\left(2\right)}}{\partial y_j}+f_i\right)+\dots =0 \]$

(14)

As Eq. (14) is applicable for every given ε→0, every coefficient of the powers of ε is zero. Therefore, we can express the problem as:

$\[ \frac{\partial {\sigma }_{ij}^{\left(0\right)}}{\partial y_j}=0 \]$

(15)

$\[ \frac{\partial {\sigma }_{ij}^{\left(0\right)}}{\partial x_j}+\frac{\partial {\sigma }_{ij}^{\left(1\right)}}{\partial y_j}=0 \]$

(16)

$\[ \frac{\partial {\sigma }_{ij}^{\left(1\right)}}{\partial x_j}+\frac{\partial {\sigma }_{ij}^{\left(2\right)}}{\partial y_j}+f_i=0 \]$

(17)

If we consider the Dirichlet and Neumann boundary conditions in Eq. (7) along with Eq. (8), boundary conditions can be expressed as follow:

$\[ {\epsilon }^0{u}_i^{\left(0\right)}+{\epsilon }^1{u}_i^{\left(1\right)}+{\epsilon }^2{u}_i^{\left(2\right)}+\dots ={\stackrel{-}{u}}_i in {\Gamma }_u \]$

(18)

$\[ \left({\epsilon }^{-1}{\sigma }_{ij}^{\left(0\right)}+{\epsilon }^0{\sigma }_{ij}^{\left(1\right)}+{\epsilon }^1{\sigma }_{ij}^{\left(2\right)}+\dots \right)n_j={\stackrel{-}{t}}_i \mathrm{i}\mathrm{n} {\Gamma }_t \]$

(19)

As Eq. (16) establishes the relationship between microscale and macroscale stresses, the perturbation displacement $$ u_i^{\left(1\right)}$$ in the microscale could be represented as follow:

$\[ u_i^1 \left(x,y\right)=-{\chi }_i^{kl}\left(y\right)\frac{\partial u_k^{\left(0\right)}}{d{x}_1}\left(x\right)+{\tilde{u}}_i^{\left(1\right)}\left(x\right) \]$

(20)

where integration constants are represented by $$ {\tilde{u}}_i^{\left(1\right)}$$ (x) in y_i, typically assumed to be zero, and $$ {\chi }_i^{kl}$$ denotes the Y-periodic components of the field tensor χ. Then, the field tensor χ is determined by solving the variational problem:

$\[ {\int }_y D_{ijkl}\frac{\partial {\chi }_k^{mn}}{\partial y_{ı}}\frac{\partial v_i}{{\partial }_{y_j}}dy={\int }_y D_{ijmn}\frac{\partial v_i}{\partial y_j}dy\forall v_i\in V_Y \]$

(21)

Where V_Y represents every Y-periodic continuous and enough regular functions with zero average value in Y.

Replacing Eq. (20) using relation (17) and taking into account the Y periodicity of $$ u_i^2$$in y, $$ \partial {\sigma }_{ij}^{\left(2\right)}/\partial y_i$$can be exclusively equal to zero as follow:

$\[ \frac{\partial }{\partial x_j}{D}_{ijmn}^h\frac{\partial u_m^{\left(0\right)}}{\partial x_n}+f_i=0 \]$

(22)

The mean value of a Y-periodic function ф(x,y) within the domain Y can be described as:

$\[ {\mathrm{\varphi }}_Y\frac{1}{\left|Y\right|}{\int }_y \mathrm{\varphi }\left(x,y\right)dY \]$

(23)

The homogenized effective elastic properties are attained taking into account the suitable boundary conditions described by the macroscale mathematical statement and adopting the averaging operator as:

$\[ D_{ijmn}^h=\frac{1}{\left|Y\right|}{\int }_y D_{ijkl}\left[{\delta }_{km}{\delta }_{ln}-\frac{\partial {\chi }_k^{mn}}{\partial y_{ı}}\right]dY \]$

(24)

After solving the macroscale problem, the stress and strain fields at the microscale level can be determined through a localization process. This process for stress and strain fields can be written as:

$\[ {\sigma }_{ij}^{\left(1\right)} \left(x,y\right)=D_{ijkl}\left(y\right)\left({\delta }_{km}{\delta }_{ln}-\frac{\partial {\chi }_k^{mn}}{\partial y_{ı}}\right)\frac{\partial u_m^{\left(0\right)}}{\partial x_n} \]$

(25)

$\[ {\epsilon }_{ij}^{\left(1\right)}\left(x,y\right)=\frac{1}{2}\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)\left({\delta }_{km}{\delta }_{ln}-\frac{\partial {\chi }_k^{mn}}{\partial y_l}\right)\frac{\partial u_m^{\left(0\right)}}{\partial x_n} \]$

(26)

These equations enable the calculation of stress and strain values at any specified point the macroscale model for a heterogeneous sample. More details are given by Pinho-da-Cruz et al. [21].

Then, it is possible to determine the effective elasticity properties of the scaffolds from the constitutive matrix’s inverse, which refers to the homogenized compliance matrix S^h.

$\[ S^h = \left[\begin{array}{cc}\begin{array}{ccc}\frac{1}{E_{11}}& \frac{-v_{12}}{E_{11}}& \frac{-v_{12}}{E_{11}}\\ \frac{-v_{12}}{E_{11}}& \frac{1}{E_{22} }& \frac{-v_{23}}{E_{22}}\\ \frac{-v_{12}}{E_{11}} & \frac{-v_{23}}{E_{22}}& \frac{1}{E_{33}}\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}& \begin{array}{ccc}\frac{1}{G_{12}}& 0& 0\\ 0& \frac{1}{G_{23}}& 0\\ 0& 0& \frac{1}{G_{12}}\end{array}\end{array}\right] \]$

(27)

where E₁₁ and E₂₂ and E₃₃ are the elastic modulus along the orthogonal directions. G₁₂ and G₂₃ are the shear modulus and the Poisson’s ratios associated with -v₁₂, -v₂₃.

3. Results

3.1 Fabrication of Structures Using an SLA 3D Printer

To validate the numerical result calculated by AEH method, all the structures were fabricated using an SLA 3D printer as shown in Fig. 3. The unit-cells were fabricated to possess external length of 10 mm, width of 10 mm in and height of 10 mm following the ratio depicted in Table 1.

Fig. 3

Optical images of fabricated unit-cells by SLA 3D printer: (a) SC truss, (b) BCC truss, (c) FCC truss, (d) SC-BCC truss, (e) SC-FCC truss

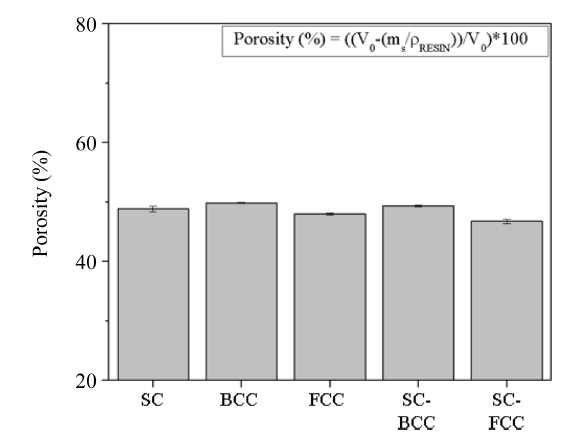
The porosity of each fabricated unit-cell was measured and averaged from 5 samples, and it was confirmed that all the unit-cells had similar porosity of 50% as depicted in Fig. 4.

Fig. 4

Measured porosity of fabricated unit-cells

3.2 Effective Stiffness Calculated by AEH Method and Using UTM Equipment

The effective elastic modulus calculated by AEH method of the unit-cell SC truss, BCC truss, SC-BCC truss, FCC truss, and SC-FCC truss is depicted in Fig. 5 and Table 2.

Fig. 5

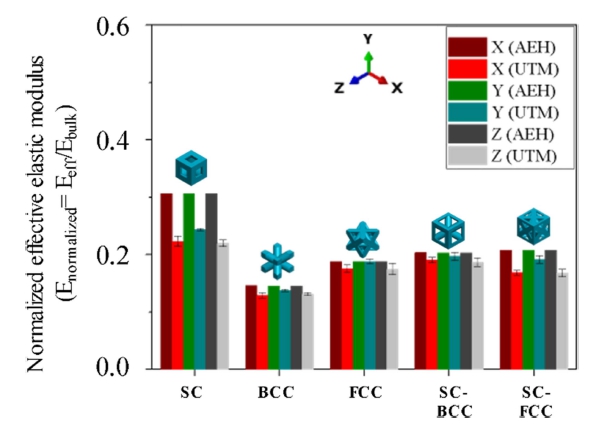
Normalized effective elastic modulus results of the different types of unit-cells by AEH method and UTM experiment

Table 2

Normalized effective stiffness of unit-cell by AEH method

The fabricated unit-cells were tested using the universal testing machine equipment (MTS-E42) under a compression load of 5 kN using 10% strain at a constant strain rate of 1 mm/min. The compressive stiffness results of the unit-cell obtained from the UTM were calculated as the average of five specimens and results are depicted in Fig. 5 and in Table 3.

Table 3

Normalized effective stiffness of open-pore unit-cell by UTM experiment

4. Discussion

This study aimed to evaluate the effective stiffness of different lattice structures using a numerical model based in asymptotic homogenization method.

To get rid of the influence of the porosity in the effective stiffness, we first confirmed that the porosity of the SC truss, BCC truss, SC-BCC truss, FCC truss, and SC-FCC specimens were fabricated very similar to that of the designed models as depicted in Fig. 4. The porosity relative error of the SC truss, BCC truss, SC-BCC truss, FCC truss, and SC-FCC truss specimens were calculated to be 2.29, 0.26, 3.96, 1.30, and 6.49% respectively. This porosity error could result from material residual between the strand and the residual of material used to support the specimens when they were printed.

With regard to effective stiffness calculated by AEH method, the results agree with previous reported studies where the mechanical properties of the SC truss, BCC truss, SC-BCC truss, FCC truss, and SC-FCC truss structures were studied using different methods such as analytical, experimental and FEM analysis [3-8]. In addition, to validate the numerical results based on AEH method in this study, the UTM experiment was carried out.

To clearly compare the results obtained by AEH method and UTM experiment, the results were characterized in term of normalized elastic modulus. The normalized elastic modulus was determined in function of the bulk material elastic modulus and the elastic modulus calculated by AEH method and UTM experiment, and it can be expressed as:

where E_normalized is the normalized elastic modulus, E_eff is the effective elastic modulus calculated by AEH method and UTM experiment and E_bulk is the elastic modulus of the bulk material. Fig. 5 summarizes the numerical results calculated by AEH method and experiments expressed as normalized effective elastic modulus and it is observed that the results attained by experiments exhibit similar trend as the numerical results based on AEH method.

The numerical elastic modulus of the SC truss unit-cell in X direction was analyzed to have 1.38 times greater stiffness than that of the experiment result, superior to 1.26 times in Y direction and 1.39 in Z direction. The BCC truss unit-cell in X direction was analyzed to have 1.13 times greater stiffness than that of the experiment result, 1.06 time higher in Y direction and 1.11 in Z direction. The FCC truss unit-cell in X direction was analyzed to have 1.07 times higher stiffness than that of the experiment result, same stiffness in Y direction and 1.08 higher in Z direction. The SC-BCC truss unit-cell in X direction was analyzed to have 1.07 times higher stiffness than that of the experiment result, over 1.03 times in Y direction and 1.09 in Z direction. The SC-FCC truss unit-cell in X direction was analyzed to have 1.23 times greater stiffness than that of the experiment result, 1.09 time higher in Y direction and 1.24 in Z direction. The average elastic modulus relative error in all directions between the AEH method and UTM experiment of the SC truss, BCC truss, FCC truss, SC-FCC truss and SC-FCC truss unit-cell was calculated to be 25.4, 8.9, 4.6, 5.7, and 15.3% respectively.

The discrepancy observed among experiments and numerical analysis results can be attributed to defects generated during the fabrication process and because in this study the compressive test was performed to a single unit-cell without having periodic arrangement of several unit-cells. Wu et al. investigated the response of material anisotropy and size effect on the mechanical properties of three types of 3D cellular structures and they reported that all the three types of structures exhibit varying levels of size effect dependency [36]. In our study, as shown in Fig. 5, the significant difference in elastic modulus observed in SC truss unit-cell compared to the other structures between simulation and experiment could be attributed primarily to the size effect, which level of size effect dependency is more prominent in the SC truss unit-cell. And in the same way as in the other structures, the structural integrity of the SC unit-cell is susceptible to structural defects or imperfections during fabrication process, which influence its mechanical behavior. Therefore, the combined influence of these two conditions could lead to bigger discrepancy between SC truss unit-cell numerical results and experimental results compared with the other structures.

5. Conclusion

We confirmed that the asymptotic expansion homogenization method is an accurate and efficient approach to predict the effective mechanical properties of lattice structures. Using this method, we analyzed several lattice structures and combining with additive manufacturing, these structures were fabricated. Moreover, the AEH method results were validated by UTM experiments, and it was found that experimental results are similar to the numerical results based on AEH method.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (Nos. NRF-2021R1A2C2009665 and NRF-2022R1A4A1028747).

REFERENCES

• Liu, Z., Liu, P., Huang, W., Wong, W. H., Commillus, A. L., Zhang, Y.-W., (2018), A nanolattice-plate hybrid structure to achieve a nearly linear relation between stiffness/strength and density, Materials & Design, 160, 496-502. [https://doi.org/10.1016/j.matdes.2018.09.039]
• Hu, Z., Thiyagarajan, K., Bhusal, A., Letcher, T., Fan, Q. H., Liu, Q., Salem, D., (2017), Design of ultra-lightweight and high-strength cellular structural composites inspired by biomimetics, Composites Part B: Engineering, 121, 108-121. [https://doi.org/10.1016/j.compositesb.2017.03.033]
• Lei, H., Li, C., Meng, J., Zhou, H., Liu, Y., Zhang, X., Wang, P., Fang, D., (2019), Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis, Materials & Design, 169, 107685. [https://doi.org/10.1016/j.matdes.2019.107685]
• Tancogne-Dejean, T., Mohr, D., (2018), Elastically-isotropic elementary cubic lattices composed of tailored hollow beams, Extreme Mechanics Letters, 22, 13-18. [https://doi.org/10.1016/j.eml.2018.04.005]
• Tancogne-Dejean, T., Mohr, D., (2018), Elastically-isotropic truss lattice materials of reduced plastic anisotropy, International Journal of Solids and Structures, 138, 24-39. [https://doi.org/10.1016/j.ijsolstr.2017.12.025]
• Li, X., Tan, Y. H., Wang, P., Su, X., Willy, H. J., Herng, T. S., Ding, J., (2020), Metallic microlattice and epoxy interpenetrating phase composites: Experimental and simulation studies on superior mechanical properties and their mechanisms, Composites Part A: Applied Science and Manufacturing, 135, 105934. [https://doi.org/10.1016/j.compositesa.2020.105934]
• Song, K., Li, D., Liu, T., Zhang, C., Xie, Y. M., Liao, W., (2022), Crystal-twinning inspired lattice metamaterial for high stiffness, strength, and toughness, Materials & Design, 221, 110916. [https://doi.org/10.1016/j.matdes.2022.110916]
• Libonati, F., Graziosi, S., Ballo, F., Mognato, M., Sala, G., (2021), 3D-printed architected materials inspired by cubic Bravais lattices, ACS Biomaterials Science & Engineering, 3935-3944. [https://doi.org/10.1021/acsbiomaterials.0c01708]
• Gibson, L. J., Ashby, M. F., (1999), Cellular solids: Structure and Properties, Cambridge University Press, 28(4), 270-274.
• Masters, I., Evans, K., (1996), Models for the elastic deformation of honeycombs, Composite Structures, 35(4), 403-422. [https://doi.org/10.1016/S0263-8223(96)00054-2]
• Christensen, R. M., (2000), Mechanics of cellular and other low-density materials, International Journal of Solids and Structures, 37(1-2), 93-104. [https://doi.org/10.1016/S0020-7683(99)00080-3]
• Wang, A.-J., McDowell, D., (2004), In-plane stiffness and yield strength of periodic metal honeycombs, Journal of Engineering Materials and Technology, 126(2), 137-156. [https://doi.org/10.1115/1.1646165]
• Chen, J., Huang, Y., Ortiz, M., (1998), Fracture analysis of cellular materials: A strain gradient model, Journal of the Mechanics and Physics of Solids, 46(5), 789-828. [https://doi.org/10.1016/S0022-5096(98)00006-4]
• Kumar, R. S., McDowell, D. L., (2004), Generalized continuum modeling of 2-D periodic cellular solids, International Journal of Solids and Structures, 41(26), 7399-7422. [https://doi.org/10.1016/j.ijsolstr.2004.06.038]
• Warren, W. E., Byskov, E., (2002), Three-fold symmetry restrictions on two-dimensional micropolar materials, European Journal of Mechanics-A/Solids, 21(5), 779-792. [https://doi.org/10.1016/S0997-7538(02)01236-6]
• Abueidda, D. W., Elhebeary, M., Shiang, C.-S. A., Pang, S., Al-Rub, R. K. A., Jasiuk, I. M., (2019), Mechanical properties of 3D printed polymeric Gyroid cellular structures: Experimental and finite element study, Materials & Design, 165, 107597. [https://doi.org/10.1016/j.matdes.2019.107597]
• Schipani, R., Nolan, D. R., Lally, C., Kelly, D. J., (2020), Integrating finite element modelling and 3D printing to engineer biomimetic polymeric scaffolds for tissue engineering, Connective Tissue Research, 61(2), 174-189. [https://doi.org/10.1080/03008207.2019.1656720]
• Wickeler, A. L., Naguib, H. E., (2020), Novel origami-inspired metamaterials: Design, mechanical testing and finite element modelling, Materials & Design, 186, 108242. [https://doi.org/10.1016/j.matdes.2019.108242]
• Li, C., Lei, H., Zhang, Z., Zhang, X., Zhou, H., Wang, P., Fang, D., (2020), Architecture design of periodic truss-lattice cells for additive manufacturing, Additive Manufacturing, 34, 101172. [https://doi.org/10.1016/j.addma.2020.101172]
• Kumar, A., Collini, L., Daurel, A., Jeng, J.-Y., (2020), Design and additive manufacturing of closed cells from supportless lattice structure, Additive Manufacturing, 33, 101168. [https://doi.org/10.1016/j.addma.2020.101168]
• Pinho-da-Cruz, J., Oliveira, J., Teixeira-Dias, F., (2009), Asymptotic homogenisation in linear elasticity. Part I: Mathematical formulation and finite element modelling, Computational Materials Science, 45(4), 1073-1080. [https://doi.org/10.1016/j.commatsci.2009.02.025]
• Oliveira, J., Pinho-da-Cruz, J., Teixeira-Dias, F., (2009), Asymptotic homogenisation in linear elasticity. Part II: Finite element procedures and multiscale applications, Computational Materials Science, 45(4), 1081-1096. [https://doi.org/10.1016/j.commatsci.2009.01.027]
• Drugan, W. J., Willis, J. R., (1996), A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites, Journal of the Mechanics and Physics of Solids, 44(4), 497-524. [https://doi.org/10.1016/0022-5096(96)00007-5]
• Kanit, T., Forest, S., Galliet, I., Mounoury, V., Jeulin, D., (2003), Determination of the size of the representative volume element for random composites: Statistical and numerical approach, International Journal of Solids and Structures, 40(13-14), 3647-3679. [https://doi.org/10.1016/S0020-7683(03)00143-4]
• Hassani, B., Hinton, E., (1998), A review of homogenization and topology opimization II—analytical and numerical solution of homogenization equations, Computers & Structures, 69(6), 719-738. [https://doi.org/10.1016/S0045-7949(98)00132-1]
• de Macedo, R. Q., Ferreira, R. T. L., Guedes, J. M., Donadon, M. V., (2017), Intraply failure criterion for unidirectional fiber reinforced composites by means of asymptotic homogenization, Composite Structures, 159, 335-349. [https://doi.org/10.1016/j.compstruct.2016.08.027]
• de Macedo, R. Q., Ferreira, R. T. L., Donadon, M. V., Guedes, J. M., (2018), Elastic properties of unidirectional fiber-reinforced composites using asymptotic homogenization techniques, Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40, 255. [https://doi.org/10.1007/s40430-018-1174-9]
• Kalamkarov, A. L., Georgiades, A., Rokkam, S., Veedu, V., Ghasemi-Nejhad, M., (2006), Analytical and numerical techniques to predict carbon nanotubes properties, International journal of Solids and Structures, 43(22-23), 6832-6854. [https://doi.org/10.1016/j.ijsolstr.2006.02.009]
• Song, Y. S., Youn, J. R., (2006), Modeling of effective elastic properties for polymer based carbon nanotube composites, Polymer, 47(5), 1741-1748. [https://doi.org/10.1016/j.polymer.2006.01.013]
• Kalamkarov, A., Georgiades, A., (2004), Asymptotic homogenization models for smart composite plates with rapidly varying thickness: Part I—Theory, International Journal for Multiscale Computational Engineering, 2(1), 133-148. [https://doi.org/10.1615/IntJMultCompEng.v2.i1.90]
• Georgiades, A., Kalamkarov, A., (2004), Asymptotic homogenization models for smart composite plates with rapidly varying thickness: Part II—Applications, International Journal for Multiscale Computational Engineering, 2(1), 149-172. [https://doi.org/10.1615/IntJMultCompEng.v2.i1.100]
• Challagulla, K. S., Georgiades, A., Kalamkarov, A., (2007), Asymptotic homogenization modeling of thin composite network structures, Composite Structures, 79(3), 432-444. [https://doi.org/10.1016/j.compstruct.2006.02.017]
• Singh, T., Kumar, S., Sehgal, S., (2020), 3D printing of engineering materials: A state of the art review, Materials today: Proceedings, 28(3), 1927-1931. [https://doi.org/10.1016/j.matpr.2020.05.334]
• Cosmi, F., Dal Maso, A., (2020), A mechanical characterization of SLA 3D-printed specimens for low-budget applications, Materials Today: Proceedings, 32, 194-201. [https://doi.org/10.1016/j.matpr.2020.04.602]
• Hada, T., Kanazawa, M., Iwaki, M., Arakida, T., Soeda, Y., Katheng, A., Otake, R., Minakuchi, S., (2020), Effect of printing direction on the accuracy of 3D-printed dentures using stereolithography technology, Materials, 13(15), 3405. [https://doi.org/10.3390/ma13153405]
• Wu, Y., Yang, L., (2021), Modeling and analysis of material anisotropy-topology effects of 3D cellular structures fabricated by powder bed fusion additive manufacturing, International Journal of Mechanical Sciences, 197, 106325. [https://doi.org/10.1016/j.ijmecsci.2021.106325]